实验目录
一、单纯形法
1. 介绍
| 单纯形法 | 它是一种解线性规划多变量模型的常用方法，是通过一种数学的迭代过程，逐步求得最优解的方法。 |
|---|
2.单纯形法的基本思想
单纯形法的基本思想是先找出一个基本可行解，对它进行鉴别，看是否是最优解；若不是，则按照一定法则转换到另一改进的基本可行解，再鉴别；若仍不是，则再转换，按此重复进行。
3.单纯形法求解步骤
①初始基可行解的确定
②求出基可行解
③最优性检验
④换基变量
⑤迭代运算。
- 例题：（我用下面这个例题来对这四种求解线性规划中的单纯形法统一进行比较，我觉得这样效果更加的明确、直观和对各种方法的对比更有针对性！）
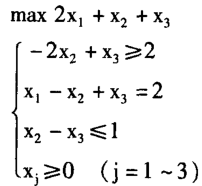
该题的结果应为：最优解为x1=x2=0,x3=2,最优值为2
二、线性规划中的单纯形法、大M法的excel求解、python编程求解和python包求解；
1. 大M法的excel求解
- 大M单纯形
- 大M算法步骤
- 我的excel表格已经放在百度网盘，需要的可以自行点击下面
大M法和“规划求解”包做的excel求解
提取码：y2w3
2.“规划求解”包做
-
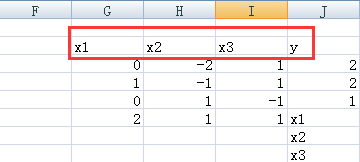
首先根据数学模型在在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项：
-
将目标方程和约束条件的对应公式输入各单元格中
K2=MMULT(G6:I6,K6:K8);
K3=MMULT(G3:I3,K6:K8);
K4=MMULT(G4:I4,K6:K8);
K5=MMULT(G5:I5,K6:K8); -
线性规划问题的电子表格模型建好后，即可利用“线性规划”功能进行求解。
然后点击数据，然后点击规划求解，如图
-
选择“工具”→“规划求解”出现“规划求解参数”窗口
-
在该对话框中，目标单元格选择K2，问题类型选择“最大值”，可变单元格选择$K K$8，点击“添加”按钮，弹出“添加约束条件”窗口
-
根据所建模型，共有4个约束条件，针对约束（1）：
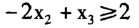，左端“单元格所引用位置”选择K3，右端“约束值”选择J3，符号类
型选择“>=”，同理继续添加约束（2）（3）（4），完成后选择“确定”，回到“规划求解参数”对话框
-
点击“选项”按钮，弹出“规划求解选项”对话框，选择“采用线性模型”和“假定非负”两项
-
点击“确定”→“求解”，选择“运算结果报告”“敏感性报告”“极限值报告”三项，最后点击“确定”
“规划求解”包做结果如下
运算结果报告 1
敏感性报告 1
极限值报告 1
3.python编程求解
- 代码如下
# encoding=utf-8
import numpy as np # python 矩阵操作lib
class Simplex():
def __init__(self):
self._A = "" # 系数矩阵
self._b = "" #数组
self._c = '' # 约束
self._B = '' # 基变量的下标集合
self.row = 0 # 约束个数
def solve(self):
# 读取文件内容，文件结构前两行分别为 变量数 和 约束条件个数
# 接下来是系数矩阵
# 然后是b数组
# 然后是约束条件c
# 假设线性规划形式是标准形式（都是等式）
A = []
b = []
c = []
self._A = np.array(A, dtype=float)
self._b = np.array(b, dtype=float)
self._c = np.array(c, dtype=float)
self._A = np.array([[0,2,-1],[0,1,-1]],dtype=float)
self._b = np.array([-2,1],dtype=float)
self._A = np.array([[1,-1,1]])# 等式约束系数self._A，3x1维列向量
self._b = np.array([2])# 等式约束系数self._b，1x1数值
self._c = np.array([2,1,1],dtype=float)
self._B = []
self.row = len(self._b)
self.var = len(self._c)
(x, obj) = self.Simplex(self._A, self._b, self._c)
self.pprint(x, obj, A)
def pprint(self, x, obj, A):
px = ['x_%d = %f' % (i + 1, x[i]) for i in range(len(x))]
print(','.join(px))
print('objective value is : %f' % obj)
print('------------------------------')
for i in range(len(A)):
print('%d-th line constraint value is : %f' % (i + 1, x.dot(A[i])))
def InitializeSimplex(self, A, b):
b_min, min_pos = (np.min(b), np.argmin(b)) # 得到最小bi
# 将bi全部转化成正数
if (b_min < 0):
for i in range(self.row):
if i != min_pos:
A[i] = A[i] - A[min_pos]
b[i] = b[i] - b[min_pos]
A[min_pos] = A[min_pos] * -1
b[min_pos] = b[min_pos] * -1
# 添加松弛变量
slacks = np.eye(self.row)
A = np.concatenate((A, slacks), axis=1)
c = np.concatenate((np.zeros(self.var), np.ones(self.row)), axis=0)
# 松弛变量全部加入基,初始解为b
new_B = [i + self.var for i in range(self.row)]
# 辅助方程的目标函数值
obj = np.sum(b)
c = c[new_B].reshape(1, -1).dot(A) - c
c = c[0]
# entering basis
e = np.argmax(c)
while c[e] > 0:
theta = []
for i in range(len(b)):
if A[i][e] > 0:
theta.append(b[i] / A[i][e])
else:
theta.append(float("inf"))
l = np.argmin(np.array(theta))
if theta[l] == float('inf'):
print('unbounded')
return False
(new_B, A, b, c, obj) = self._PIVOT(new_B, A, b, c, obj, l, e)
e = np.argmax(c)
# 如果此时人工变量仍在基中，用原变量去替换之
for mb in new_B:
if mb >= self.var:
row = mb - self.var
i = 0
while A[row][i] == 0 and i < self.var:
i += 1
(new_B, A, b, c, obj) = self._PIVOT(new_B, A, b, c, obj, new_B.index(mb), i)
return (new_B, A[:, 0:self.var], b)
# 算法入口
def Simplex(self, A, b, c):
B = ''
(B, A, b) = self.InitializeSimplex(A, b)
# 函数目标值
obj = np.dot(c[B], b)
c = np.dot(c[B].reshape(1, -1), A) - c
c = c[0]
# entering basis
e = np.argmax(c)
# 找到最大的检验数，如果大于0，则目标函数可以优化
while c[e] > 0:
theta = []
for i in range(len(b)):
if A[i][e] > 0:
theta.append(b[i] / A[i][e])
else:
theta.append(float("inf"))
l = np.argmin(np.array(theta))
if theta[l] == float('inf'):
print("unbounded")
return False
(B, A, b, c, obj) = self._PIVOT(B, A, b, c, obj, l, e)
e = np.argmax(c)
x = self._CalculateX(B, A, b, c)
return (x, obj)
# 得到完整解
def _CalculateX(self, B, A, b, c):
x = np.zeros(self.var, dtype=float)
x[B] = b
return x
# 基变换
def _PIVOT(self, B, A, b, c, z, l, e):
# main element is a_le
# l represents leaving basis
# e represents entering basis
main_elem = A[l][e]
# scaling the l-th line
A[l] = A[l] / main_elem
b[l] = b[l] / main_elem
# change e-th column to unit array
for i in range(self.row):
if i != l:
b[i] = b[i] - A[i][e] * b[l]
A[i] = A[i] - A[i][e] * A[l]
# update objective value
z -= b[l] * c[e]
c = c - c[e] * A[l]
# change the basis
B[l] = e
return (B, A, b, c, z)
s = Simplex()
s.solve()
运行的结果：
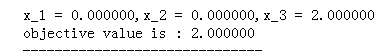
4.python包scipy求解
例 python包求解下列线性规划问题
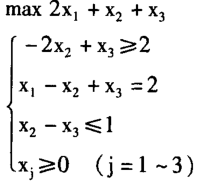
- 导入相关的包，需要scipy和numpy库
import numpy as np
from scipy import optimize as op
- 给出变量取值范围
# 给出变量取值范围
x1=(0,None)
x2=(0,None)
x3=(0,None)
- 定义给出变量，确定c,A_ub,B_ub,A_eq,B_eq
c = np.array([2,1,1])# 目标函数系数,3x1列向量
A_ub = np.array([[0,2,-1],[0,1,-1]]) # 不等式约束系数A，2x3维矩阵
B_ub = np.array([-2,1])# 等式约束系数B, 2x1维列向量
A_eq = np.array([[1,-1,1]])# 等式约束系数Aeq，3x1维列向量
B_eq = np.array([2])# 等式约束系数beq，1x1数值
- 调用函数进行求解
res=op.linprog(c,A_ub,B_ub,A_eq,B_eq,bounds=(x1,x2,x3))#调用函数进行求解
res
结果如图：
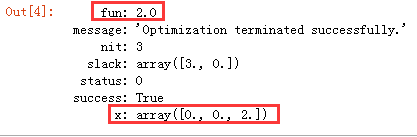
整体代码及运行结果如下
5.前4种的结果对比与总结
可以看出，用大M法的excel求解、规划求解、python编程求解和python包分别求解线性规划中的单纯形法方法算出来的解均相同，都是x1=x2=0,x3=2,最优值为2，但是我觉得“规划求解”直接调用包要更简单，python求解单纯形法调用包做也是比较简单，步骤也很好理解，但其中所用的优化思想应该值得好好体会！
三、参考文献
点击
（ 非线性规划的拉格朗日乘子法）
- 在另外一篇博客里面！
加 油 ! ! !