稀疏贝叶斯学习 2

稀疏贝叶斯学习 2

快速 RVM 贝叶斯学习算法

对于最原始的稀疏表示问题，其拉格朗日形式可写为：
$\begin{aligned} \hat{\mathbf s} =\underset{\mathbf s}{\arg\min} \Big\Vert \mathbf y - \mathbf A \mathbf s \Big \Vert_2^2 +\lambda \Vert \mathbf s\Vert_0 \end{aligned}$

可以看出，如果将 $\Big\Vert \mathbf y - \mathbf A \mathbf s \Big \Vert_2^2$ 看作 $\mathbf s$ 的负高斯对数似然函数，而将 $\lambda \Vert \mathbf s\Vert_0$ 等价于是 $\mathbf s$ 的先验分布的负对数，那么上面的优化问题实际上可解释为一个贝叶斯过程。进一步分析，求最稀疏解的问题就是一个最大后验概率（MAP：Maximum a Posteriori）估计问题。

以上分析可得出两个结论：

• 常见的稀疏优化问题均可以利用贝叶斯参数估计来统一表示
• 不同的先验概率假设会产生不同的约束效果

因此合理的先验假设是贝叶斯学习有效进行的关键。

常用的贝叶斯先验假设方法有以下几种：

• 贝叶斯 $\mathcal L_p$ 范数包括针对不同优化范数的贝叶斯 Lasso、推广的 Bayes 弹性网等，这类方法基于合理的假设，通过积分计算后验达到与所求范数近似的形式，从而实现 Bayes 范数。

• 在基于高斯先验的稀疏表示模型中，假设要估计的稀疏向量 $\mathbf s$ 的各个元素相互独立，且服从高斯分布 $\mathcal N(0, \sigma_n^2)$，对于 $\sigma_n^2$，可采用标准伽马函数、标准逆高斯函数或 Jeffreys 函数 $p(\sigma_n^2) \propto 1/\sigma_n^2$ 作为其先验，然后计算相应的后验估计。

• 相关向量机 RVM 是一种与 SVM 类似的稀疏概率模型，其实质是一种新的贝叶斯框架下的监督学习方法。RVM 是通过多次计算参数相关性，移除不相关的基原子，从而逼近稀疏解。首先假设待估计向量中的任意一个元素都满足 Gaussian 先验分布，同时先验分布中的参数服从一个 Gamma 分布，然后计算 Gamma 分布中超参数的边缘分布，利用最大化后验概率（MAP）迭代求解出未知参数向量的均值与方差，并且利用均值进一步估计参数。该方法避免了 Laplace 先验产生的计算难度，而且可以获得信号和噪声的准确估计。

在贝叶斯学习的稀疏重构算法研究中,当前有两大热点：

• 相关向量机的监督学习方法
• 非参数贝塔过程的稀疏建模表示

RVM 相关向量机

稀疏贝叶斯学习（SBL）是一个强大的贝叶斯变量选择方法论，特别是当有用的变量数量很少时，优势极为突出。研究人员将 SBL 引入到稀疏信号恢复领域，作为稀疏线性回归模型中基选择的方法。

给定
$\mathbf t = \mathbf y+\mathbf z=\mathbf \Phi \mathbf w +\mathbf z$

其中

• $\mathbf z=[z_1,\cdots, z_N]^{\rm T}$ 表示方差未知的近似高斯噪声
  • $p(\mathbf z)=\prod_{n=1}^{N} \mathcal N(z_n\vert 0, \sigma^2)$
• $\mathbf y=\sum_{m=1}^{M}w_m \boldsymbol\phi_m =\mathbf \Phi \mathbf w$
  • $\mathbf w =[w_1,\cdots, w_M]^{\rm T}$ 是参数向量
  • $\mathbf \Phi =[\boldsymbol\phi_1,\cdots, \boldsymbol\phi_M]$ 是 $N \times M$ 的矩阵
  • $\boldsymbol\phi_M$ 代表 第 $M$ 个 基向量

在这里，一般 $\mathbf \Phi$ 都是核函数构成的：

$\mathbf \Phi= \begin{bmatrix} 1&K(\mathbf x_1,\mathbf x_1)&K(\mathbf x_1,\mathbf x_2)& \cdots &K(\mathbf x_1,\mathbf x_M)\\ 1&K(\mathbf x_2,\mathbf x_1)&K(\mathbf x_2,\mathbf x_2)& \cdots& K(\mathbf x_2,\mathbf x_M)\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1&K(\mathbf x_N,\mathbf x_1)&K(\mathbf x_N,\mathbf x_2)& \cdots &K(\mathbf x_N,\mathbf x_M)\\ \end{bmatrix}$
于是 $\mathbf \Phi =[\boldsymbol\phi(\mathbf x_1),\cdots, \boldsymbol\phi(\mathbf x_N)]^{\rm T}$：
$\boldsymbol\phi(\mathbf x_i) = \begin{bmatrix} 1 \\ K(\mathbf x_i,\mathbf x_1) \\ K(\mathbf x_i,\mathbf x_2) \\ \vdots \\ K(\mathbf x_i,\mathbf x_M) \end{bmatrix}$

---

于是引入针对目标向量 $\mathbf t$ 的多变量高斯似然模型
$p(\mathbf t \vert \mathbf w, \sigma^2) =(2\pi \sigma^2)^{-\frac{N}{2}} \exp \left( -\frac{\Vert \mathbf t - \mathbf \Phi \mathbf w \Vert^2}{2 \sigma^2} \right)$

式中权值 $\mathbf w$ 和噪声方差 $\sigma^2$ 是待估计的量，根据以上分析，就是要寻找一个后验密度函数。如何应用贝叶斯估计理论，得到 $\mathbf w$ 和 $\sigma^2$ 的后验估验估计呢？可以用相关向量机（RVM）来实现，其本质是使后验概率最大化来求解相关向量的加权值。

如果采用常见的最大似然法（ML）求解待估计的 $\mathbf w$ 和 $\sigma^2$，为了避免过学习现象，因此在 RVM 框架中，我们给 $\mathbf w$ 加上一个先决条件，具体来说，首先对 $\mathbf w$ 的各个元素赋予均值为 0，方差为 $\alpha_i^{-1}$ 的高斯先验，即
$\begin{aligned} p(\mathbf w \vert \boldsymbol\alpha) &=(2\pi)^{-\frac{M}{2}} \prod_{m=1}^{M} \alpha_m^{1/2} \exp \left( -\frac{\alpha_m w_m^2 }{2} \right) \\ &= \prod_{i=1}^{M} \mathcal N(w_i \vert 0, \alpha_i^{-1}) \\ &=(2\pi)^{\frac{-M}{2}} \Big\vert \mathbf{\Lambda}_{\alpha} \Big\vert^{-\frac{1}{2}} \exp\left({-\frac{1}{2}\mathbf{ w}^{\rm T}\mathbf{\Lambda_{\alpha}^{-1}\mathbf{ w}}} \right) \end{aligned}$
其中 $\mathbf{\Lambda}_{\alpha}=\text{diag}([\alpha_1^{-1},\cdots,\alpha_M^{-1}])$。

其次再对 $\boldsymbol \alpha$ 赋 Gamma 先验，即：
$p(\boldsymbol\alpha) = \prod_{i=1}^{M} \Gamma(\alpha_i \vert a,b) = p(\boldsymbol\alpha \vert a,b)$
其中，Gamma 分布的形式为
$\Gamma(x \vert a,b) = \frac{ b^a x^{a-1}e^{-bx}}{f_{\Gamma}(a)}$
关于 Gamma 分布的来历，可以参考链接 https://blog.csdn.net/chenshulong/article/details/79027103。
其中 Gamma 函数是 $f_{\Gamma}(x) =\int_0^{\infty}t^{x-1}e^{-t} \text{d}t$。具有的性质为：

• $f_{\Gamma}(x+1) =x f_{\Gamma}(x)$
• $f_{\Gamma}(n) = (n-1)!$

---

结合 $p(\mathbf w \vert \boldsymbol\alpha)$ 和 $p(\boldsymbol\alpha \vert a,b)$， 可得
$p(\mathbf w \vert a,b)= \prod_{i=1}^{M} \int_{0}^{\infty} \mathcal N(w_i \vert 0, \alpha_i^{-1}) \Gamma(\alpha_i \vert a,b) \text{d}\alpha_i$
于是，通过求解 $\boldsymbol\alpha$ 参数，进一步可得到 $\mathbf w$ 的解。实验证明，上述超参数求解过程中，大部分的 $\alpha_i$ 会变得无限大，这意味着与该 $\alpha_i$ 相关的参数 $w_i$ 的先验服从于 $p(w_i)=\mathcal{N}(0,\alpha_i^{-1})$ 其中 $\alpha_i$ 无限大，则可以证明 $p(w_i)$ 的后验分布也服从零均值，零方差的高斯正态分布，这意味着 $w_i=0$。

SBL 贝叶斯学习算法

下面详细介绍基于 RVM 机制的快速贝叶斯学习算法（FSBL）。根据贝叶斯稀疏重构理论， 可以通过统计概率方法解决，即：
$\hat{\mathbf w} =\underset{{\mathbf w} }{\arg\max} \Big[ p( \hat{\mathbf w}, \sigma^2, \boldsymbol \alpha\vert \mathbf t) \Big]$
这里的 $\boldsymbol \alpha$ 为参数向量，它决定估计向量的稀疏度，根据贝叶斯定理：
$\boxed{ \textcolor{blue}{ p( \hat{\mathbf w}, \sigma^2, \boldsymbol \alpha\vert \mathbf t) = p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) p( \sigma^2, \boldsymbol \alpha \vert \mathbf t) } }$

接下来我们主要围绕上面这个公式展开推导

• 首先从公式的第一项 $p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t)$ 开始分析。
• 然后分析第二项 $p( \sigma^2, \boldsymbol \alpha \vert \mathbf t)$。

第一项

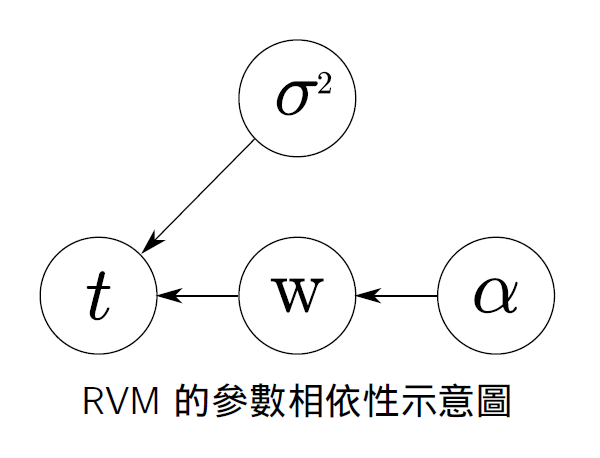
根据上面示意图中的概率依赖关系，其中
$\begin{aligned} p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) &= \frac{p( {\mathbf w},\mathbf t \vert \sigma^2, \boldsymbol \alpha) }{p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)} \\ &=\frac{p(\mathbf w \vert \boldsymbol\alpha) p(\mathbf t \vert \mathbf w, \sigma^2)}{p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)} \\ &=\frac{p(\mathbf w \vert \boldsymbol\alpha) p(\mathbf t \vert \mathbf w, \sigma^2)}{\int p(\mathbf w \vert \boldsymbol\alpha) p(\mathbf t \vert \mathbf w, \sigma^2) \text{d}\mathbf w} \\ &=(2\pi)^{-\frac{M}{2}} \Big\vert \mathbf \Sigma \Big\vert^{-1/2} \exp\left\{ -\frac{1}{2} (\mathbf w- \bm{\mu})^{\rm T} \mathbf \Sigma^{-1}(\mathbf w- \bm{\mu}) \right\} \end{aligned}$

---

推导过程如下：
$\begin{aligned} p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)=\int (2\pi\sigma^2)^{-N/2}(2\pi)^{-M/2} \Big|\mathbf{\Lambda}_{\alpha}\Big|^{-\frac{1}{2}} \exp\bigg[-\frac{1}{2\sigma^2}(\mathbf{t}-\mathbf{\Phi w})^{\rm T}(\mathbf{t}-\mathbf{\Phi w})-\frac{1}{2}\mathbf {w}^{\rm T} \mathbf{\Lambda_{\alpha}^{-1} w} \bigg] \text{d}\mathbf w \end{aligned}$

其实该式可以看成两个高斯函数进行卷积，根据高斯函数性质知，两个高斯函数卷积的结果仍为高斯函数。所以只需要求得卷积后的高斯函数的均值和期望，就相当于求出上式的积分了。

取其指数，令
$\begin{aligned} Q &=-\frac{1}{2\sigma^2}(\mathbf{t}-\mathbf{\Phi w})^{\rm T}(\mathbf{t}-\mathbf{\Phi w})-\frac{1}{2}\mathbf {w}^{\rm T} \mathbf{\Lambda_{\alpha}^{-1} w} \\ &=-\frac{1}{2\sigma^2} \bigg(\mathbf t^{\rm T}\mathbf t -\mathbf t^{\rm T}\mathbf{ \Phi w}-\mathbf w^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf t \bigg) -\frac{1}{2\sigma^2}\mathbf w^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{ \Phi w}-\frac{1}{2}\mathbf {w}^{\rm T} \mathbf{\Lambda_{\alpha}^{-1} w} \\ &=-\frac{1}{2\sigma^2} \bigg[ \mathbf{w}^{\rm T}(\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1})\mathbf{w}-\mathbf{t}^{\rm T}\mathbf{\Phi}\mathbf{w}-\mathbf{w}^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{t}+\mathbf{t}^{\rm T}\mathbf{t} \bigg] \end{aligned}$
这时有
$p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)= (2\pi\sigma^2)^{-N/2}(2\pi)^{-M/2} \Big|\mathbf{\Lambda}_{\alpha}\Big|^{-\frac{1}{2}} \int \exp\bigg(Q(\mathbf w)\bigg)\text{d}\mathbf w$
注意 $Q$ 是关于 $\mathbf w$ 的二次项的函数。这里求解上述积分要用到高斯函数的以下性质：
$\int_{\bm{\omega}}\exp\left[{-(\bm{A\omega}+\bm{b})^2} \right] \text{d}\bm{\omega}=C$
在这里 $C$ 是常数，具体是多少可以不关注。现在的问题是我们需要将 $Q$ 表达成 $-(\mathbf{A w}+\mathbf{b})^2+f(\mathbf t, \sigma^2)$ 的形式，并求得 $f(t,σ2)$。显然，我们将满足 $\mathbf{A w}+\mathbf{b}=0$ 的 $\mathbf{w}$ 代入其中，即得到 $f(\mathbf t, \sigma^2)$。先求 $\mathbf{w}$，下面通过求导完成。

$\begin{aligned} \frac{dQ}{d\bf{w}}&=-\frac{1}{\sigma^2} \bigg[ (\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1})\mathbf{w}-\mathbf{\Phi}^{\rm T}\mathbf{t} \bigg]=0 \\ \mathbf w^* &=(\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1})^{\dagger} \mathbf{\Phi}^{\rm T}\mathbf{t} \end{aligned}$

由于 $\frac{dQ}{d\bf{w}}=0 \Longleftrightarrow \mathbf{A w}+\mathbf{b}=0$，令 $\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1}=\mathbf B$，从而可以将 $\mathbf w^* =\mathbf B^{\dagger} \mathbf{\Phi}^{\rm T}\mathbf{t}$ 代入到 $Q(\mathbf w)$ 中，求得
$\begin{aligned} Q(\mathbf w^*)&=-\frac{1}{2\sigma^2} \bigg[ \mathbf{w}^{\rm T}\mathbf B\mathbf{w}-\mathbf{t}^{\rm T}\mathbf{\Phi}\mathbf{w}-\mathbf{w}^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{t}+\mathbf{t}^{\rm T}\mathbf{t} \bigg] \\ &=-\frac{1}{2\sigma^2} \bigg[ \mathbf{t}^{\rm T} \left( \mathbf{I}-\mathbf{\Phi}\mathbf B^{\dagger}\mathbf{\Phi}^{\rm T} \right) \mathbf{t} \bigg] = f(\mathbf t, \sigma^2) \\ p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)&= (2\pi\sigma^2)^{-N/2}(2\pi)^{-M/2} \Big|\mathbf{\Lambda}_{\alpha}\Big|^{-\frac{1}{2}} \int \exp\bigg(Q(\mathbf w)\bigg)\text{d}\mathbf w \\ &=(2\pi\sigma^2)^{-N/2}(2\pi)^{-M/2} \Big|\mathbf{\Lambda}_{\alpha}\Big|^{-\frac{1}{2}} C \cdot \exp\bigg( -\frac{1}{2\sigma^2} \bigg[ \mathbf{t}^{\rm T} \left( \mathbf{I}-\mathbf{\Phi}\mathbf B^{\dagger}\mathbf{\Phi}^{\rm T} \right) \mathbf{t} \bigg] \bigg) \end{aligned}$
现在可以看出 $p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)$ 是一个高斯分布，其均值为 0，协方差矩阵 $\mathbf\Sigma_t$ 满足
$\begin{aligned} \mathbf\Sigma_t^{-1}=\frac{1}{\sigma^2} \left( \mathbf{I}-\mathbf{\Phi}\mathbf B^{\dagger}\mathbf{\Phi}^{\rm T} \right) \end{aligned}$
随后 $\mathbf\Sigma_t$ 可由矩阵求逆公式得到，如下：
$\begin{aligned} \mathbf\Sigma_t&={\sigma^2} \big( \mathbf{I}-\mathbf{\Phi}\mathbf B^{\dagger}\mathbf{\Phi}^{\rm T} \big)^{-1} \\ &={\sigma^2} \bigg[ \mathbf{I}-\mathbf{\Phi} \big( \mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1} \big)^{-1} \mathbf{\Phi}^{\rm T} \bigg]^{-1} \\ &=\sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \end{aligned}$

这是在写博客时候第二次遇到矩阵求逆公式；参考1；参考2：
$\boxed{ \textcolor{red}{ (\mathbf A+\mathbf{UBV})^{-1}=\mathbf A^{-1}- \mathbf A^{-1}\mathbf{UB}(\mathbf I+\mathbf{VA}^{-1}\mathbf{UB})^{-1}\mathbf{VA}^{-1} } }$
根据该公式以及 $\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1}=\mathbf B$，可以写出
$\begin{aligned} &\bigg[ \mathbf{I}-\mathbf{\Phi} \big( \mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1} \big)^{-1} \mathbf{\Phi}^{\rm T} \bigg]^{-1} \\ =& \ \ \mathbf{I}+\mathbf{\Phi} \textcolor{blue}{\mathbf B^{-1}\big( \mathbf{I} -\mathbf{\Phi}^{\rm T}\mathbf{\Phi}\mathbf B^{-1} \big)^{-1}} \mathbf{\Phi}^{\rm T} \\ =& \ \ \mathbf{I}+\mathbf{\Phi} \bigg[ \big( \mathbf{I} -\mathbf{\Phi}^{\rm T}\mathbf{\Phi}\mathbf B^{-1} \big) \mathbf B \bigg]^{-1} \mathbf{\Phi}^{\rm T} \\ =& \ \ \mathbf{I}+\mathbf{\Phi} \big( \mathbf{B} -\mathbf{\Phi}^{\rm T}\mathbf{\Phi} \big)^{-1} \mathbf{\Phi}^{\rm T} \\ =& \ \ \mathbf{I}+ \sigma^{-2}\mathbf{\Phi} \mathbf{\Lambda}_{\alpha} \mathbf{\Phi}^{\rm T} \end{aligned}$

至此，我们对于协方差的推导到此结束。

---

利用前面的结果，分母部分 $p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)$ 已求得。分子部分是两个高斯概率密度函数的乘积，其结果仍为高斯分布。再与分母部分相除，最终还是为高斯分布：
$\begin{aligned} p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) &=\frac{p(\mathbf w \vert \boldsymbol\alpha) p(\mathbf t \vert \mathbf w, \sigma^2)}{p( \mathbf t \vert \sigma^2, \boldsymbol \alpha)} \\ \end{aligned}$
结合前面已得结果：
$\boxed{ \begin{aligned} p(\mathbf w \vert \boldsymbol\alpha)&= (2\pi)^{\frac{-M}{2}} \Big\vert \mathbf{\Lambda}_{\alpha} \Big\vert^{-\frac{1}{2}} \exp\left({-\frac{1}{2}\mathbf{ w}^{\rm T}\mathbf{\Lambda_{\alpha}^{-1}\mathbf{ w}}} \right) \\ p(\mathbf t \vert \mathbf w, \sigma^2) &=(2\pi \sigma^2)^{-\frac{N}{2}} \exp \left(-\frac{1}{2\sigma^2}(\mathbf{t}-\mathbf{\Phi w})^{\rm T}(\mathbf{t}-\mathbf{\Phi w}) \right) \end{aligned} }$
令 $(2\pi\sigma^2)^{-\frac{N}{2}}(2\pi)^{-\frac{M}{2}} \Big|\mathbf{\Lambda}_{\alpha}\Big|^{-\frac{1}{2}} =C_1$，有
$\begin{aligned} p(\mathbf w \vert \boldsymbol\alpha) p(\mathbf t \vert \mathbf w, \sigma^2) &= C_1 \cdot \exp\bigg( -\frac{1}{2\sigma^2} \bigg[ \mathbf{w}^{\rm T}\mathbf B\mathbf{w}-\mathbf{t}^{\rm T}\mathbf{\Phi}\mathbf{w}-\mathbf{w}^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{t}+\mathbf{t}^{\rm T}\mathbf{t} \bigg] \bigg) \\ \textcolor{blue}{ p( \mathbf t \vert \sigma^2, \boldsymbol \alpha) } &\textcolor{blue}{=(2\pi)^{-\frac{N}{2}} \Big\vert \mathbf{\Sigma}_t \Big\vert^{-\frac{1}{2}} \exp\bigg( -\frac{1}{2} \bigg[ \mathbf{t}^{\rm T} \left( \mathbf{\Sigma}_t \right)^{-1} \mathbf{t} \bigg] \bigg) } \end{aligned}$
忽略常数部分，得
$\begin{aligned} p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) &=C_2 \exp\bigg( -\frac{1}{2\sigma^2} \bigg[ \mathbf{w}^{\rm T}\mathbf B\mathbf{w}-\mathbf{t}^{\rm T}\mathbf{\Phi}\mathbf{w}-\mathbf{w}^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{t}+\mathbf{t}^{\rm T}\mathbf{t} \bigg] -\frac{1}{2}\mathbf{t}^{\rm T} \mathbf{\Sigma}_t^{-1} \mathbf{t} \bigg) \\ &=C_2 \exp\bigg( Q_w(\mathbf w)\bigg) \end{aligned}$

根据多维高斯函数的形式
$\mathcal N(\mathbf x \vert \bm\mu,\mathbf \Sigma)= (2\pi)^{-d/2} \Big\vert \mathbf \Sigma \Big\vert^{-1/2} \exp\bigg\{ -\frac{1}{2} (\mathbf x-\bm\mu) ^{\rm T} \mathbf \Sigma^{-1} (\mathbf x-\bm\mu) \bigg\}$
令指数部分
$Q_1 =-\frac{1}{2} (\mathbf x-\bm\mu) ^{\rm T} \mathbf \Sigma^{-1} (\mathbf x-\bm\mu)$
可知
$\begin{aligned} \frac{dQ_1}{d\bf{x}}&=0 \Longrightarrow \hat{\mathbf x}_0 = \bm\mu \\ \frac{d^2Q_1}{d\mathbf{x}^2}&=- \mathbf \Sigma^{-1} \end{aligned}$

因此，可以得出 $p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t)$ 的均值 $\bm\mu_w$ 与协方差 $\mathbf \Sigma_w$：
$\begin{aligned} \frac{dQ_w}{d\bf{w}}&=0 \Longrightarrow \bm\mu_w =\mathbf B^{-1} \mathbf{\Phi}^{\rm T}\mathbf t =(\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1})^{-1} \mathbf{\Phi}^{\rm T}\mathbf t \\ -\frac{d^2Q_w}{d\mathbf{w}^2}&= \mathbf \Sigma_w^{-1} = \frac{1}{\sigma^2}\mathbf B = \frac{1}{\sigma^2} (\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\sigma^2\mathbf{\Lambda}_{\alpha}^{-1}) = \frac{1}{\sigma^2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\mathbf{\Lambda}_{\alpha}^{-1} \end{aligned}$
整理可得
$\boxed{ p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) = (2\pi)^{-\frac{M}{2}} \Big\vert \mathbf \Sigma_w \Big\vert^{-1/2} \exp\left\{ -\frac{1}{2} (\mathbf w- \bm{\mu}_w)^{\rm T} \mathbf \Sigma_w^{-1}(\mathbf w- \bm{\mu}_w) \right\} }$

其中
$\boxed{ \begin{aligned} \mathbf \Sigma_w^{-1} &= \frac{1}{\sigma^2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\mathbf{\Lambda}_{\alpha}^{-1} \\ \bm\mu_w &= \sigma^{-2} \mathbf \Sigma_w \mathbf{\Phi}^{\rm T}\mathbf t \end{aligned} }$

至此，第一项推导完毕，过程可真是长啊！

---

第二项

回顾前面提到的贝叶斯公式：
$\boxed{ \textcolor{blue}{ p( \hat{\mathbf w}, \sigma^2, \boldsymbol \alpha\vert \mathbf t) = p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) p( \sigma^2, \boldsymbol \alpha \vert \mathbf t) } }$
为什么要写这个贝叶斯式呢，因为我们最后要用到它来预测，预测的条件概率算式如下：
$\begin{aligned} p(t^{*} \vert \mathbf t) &=\int \bigg[p(t^* \vert \mathbf w, \sigma^2, \boldsymbol \alpha) p( \hat{\mathbf w}, \sigma^2, \boldsymbol \alpha\vert \mathbf t) \bigg] \text{d}\mathbf w \text{d}\boldsymbol \alpha \text{d}\sigma^2 \\ &=\int \bigg[p(t^* \vert \mathbf w, \sigma^2, \boldsymbol \alpha) p( \hat{\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) p( \sigma^2, \boldsymbol \alpha \vert \mathbf t) \bigg] \text{d}\mathbf w \text{d}\boldsymbol \alpha \text{d}\sigma^2 \end{aligned}$
前面也提到过，如果直接使用 Maximum Likelihood 的方法解 $\mathbf w$ 和 $\sigma^2$，通常会使 $\mathbf w$ 中的元素大部分都不是 0 （over fitting）。因此引入了 $\bm \alpha$。

接下来开始分析第二项 $p( \sigma^2, \boldsymbol \alpha \vert \mathbf t)$，由前面的概率依赖关系，以及贝叶斯定理，首先有
$\begin{aligned} p( \sigma^2, \boldsymbol \alpha \vert \mathbf t) &\propto p(\mathbf t \vert \bm \alpha, \sigma^2)p(\bm \alpha, \sigma^2) \\ &\propto p(\mathbf t \vert \bm \alpha, \sigma^2) p(\bm \alpha) p(\sigma^2) \end{aligned}$
注意先验 $p(\bm \alpha)$ 和 $p(\sigma^2)$ 都是常数，假设近似解 $\hat{\bm \alpha}$ 和 $\hat{\sigma}^2$ 为

$(\hat{\bm \alpha}, \hat{\sigma}^2) = \underset{\bm \alpha, \sigma^2}{\arg\max}\quad p( \boldsymbol \alpha, \sigma^2 \vert \mathbf t)$

这样条件概率表示为
$\begin{aligned} p(t^* \vert \mathbf t) &=\int \bigg[p(t^* \vert \mathbf w, \sigma^2, \boldsymbol \alpha) p( {\mathbf w} \vert \sigma^2, \boldsymbol \alpha,\mathbf t) \textcolor{blue}{ \delta(\bm \alpha -\hat{\bm \alpha}) \delta(\sigma^2- \hat{\sigma}^2) } \bigg] \text{d}\mathbf w \text{d}\boldsymbol \alpha \text{d}\sigma^2 \\ &=\int \bigg[p(t^* \vert \mathbf w, \hat{\sigma}^2, \hat{\bm \alpha}) p( {\mathbf w} \vert \hat{\sigma}^2, \hat{\bm \alpha}, \mathbf t) \bigg] \text{d}\mathbf w \end{aligned}$

根据马尔可夫性，其中
$p(t^* \vert \mathbf w, \hat{\sigma}^2, \hat{\bm \alpha})=p(t^* \vert \mathbf w, \hat{\sigma}^2)=\mathcal N(t^* \vert y^*, \hat{\sigma}^2)$

所以，上面条件概率积分式中的函数是两个 Gaussian function 的乘积。和前文中的卷积一致，根据高斯函数性质知，两个高斯函数卷积的结果仍为高斯函数。所以只需要求得卷积后的高斯函数的均值和期望，就相当于求出上式的积分了。
因此定积分以后的结果假设为：
$\begin{aligned} p(t^* \vert \mathbf t) =\mathcal N(t^* \vert y_p, \sigma_p^2) \end{aligned}$
那么 $y_p, \sigma_p^2$ 怎么求呢，这类需要引入一个推导参考。

---

通过参考《Bishop, C., 2006. Pattern recognition and machine learning. springer, New York.》下面的高斯变量的贝叶斯定理公式：

推导也可以参见链接 http://pelhans.com/2018/10/15/prml_note2/#233-高斯变量的贝叶斯定理。所以有以下结果：
$\begin{aligned} p( {\mathbf w} \vert \hat{\sigma}^2, \hat{\bm \alpha}, \mathbf t) &= \mathcal N(\mathbf w \vert \hat{\bm \mu}, \hat{\mathbf \Sigma} ) \\ \hat{\mathbf \Sigma}&= ( \hat{\sigma}^{-2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\mathbf{\Lambda}_{\alpha}^{-1} )^{-1}\\ \hat{\bm \mu}&= \hat{\sigma}^{-2} \hat{\mathbf \Sigma} \mathbf{\Phi}^{\rm T}\mathbf t\\ p(t^* \vert \mathbf w, \hat{\sigma}^2)&=\mathcal N(t^* \vert y^*, \hat{\sigma}^2) \\ y^*&= \bm \phi^{\rm T}(\mathbf x^*) \mathbf w \end{aligned}$

我们可以则可以推出均值 $y_p$ 和方差 $\sigma_p^2$：
$\boxed{ \begin{aligned} y_p &=\bm \phi^{\rm T}(\mathbf x^*) \hat{\bm \mu}= \hat{\bm \mu}^{\rm T} \bm \phi(\mathbf x^*)\\ \sigma_p^2&=\hat{\sigma}^2+\bm\phi^{\rm T}(\mathbf x^*) \hat{\mathbf \Sigma} \bm\phi(\mathbf x^*) \end{aligned} }$

求近似解

前面提到假设的近似解 $\hat{\bm \alpha}$ 和 $\hat{\sigma}^2$ 为

$(\hat{\bm \alpha}, \hat{\sigma}^2) = \underset{\bm \alpha, \sigma^2}{\arg\max}\quad p( \boldsymbol \alpha, \sigma^2 \vert \mathbf t)$

现在剩下的问题就是怎么求它们了。由前面的概率依赖关系，以及贝叶斯定理，首先有
$\begin{aligned} p( \sigma^2, \boldsymbol \alpha \vert \mathbf t) &\propto p(\mathbf t \vert \bm \alpha, \sigma^2)p(\bm \alpha, \sigma^2) \\ &\propto p(\mathbf t \vert \bm \alpha, \sigma^2) p(\bm \alpha) p(\sigma^2) \end{aligned}$
则可以通过
$(\hat{\bm \alpha}, \hat{\sigma}^2) = \underset{\bm \alpha, \sigma^2}{\arg\max}\quad p(\mathbf t \vert \bm \alpha, \sigma^2)$
不幸的是，目前没有闭式解的形式存在，只能通过数值方法求导。回顾前面已经求得的
$\begin{aligned} \textcolor{blue}{ p( \mathbf t \vert \sigma^2, \boldsymbol \alpha) } & =(2\pi)^{-\frac{N}{2}} \Big\vert \mathbf{\Sigma}_t \Big\vert^{-\frac{1}{2}} \exp\left( -\frac{1}{2} \left[ \mathbf{t}^{\rm T} \left( \mathbf{\Sigma}_t \right)^{-1} \mathbf{t} \right] \right) \\ &= \mathcal N \left(\mathbf t \Big\vert\bm 0, \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \right) \end{aligned}$
我们对其取对数，然后得到
$\begin{aligned} \mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) = {-\frac{N}{2}} \log (2\pi)-\frac{1}{2} \log\Big\vert \mathbf{\Sigma}_t \Big\vert -\frac{1}{2} \mathbf{t}^{\rm T} \mathbf{\Sigma}^{-1}_t \mathbf{t} \end{aligned}$
忽略掉与 $\hat{\bm \alpha}$ 和 $\hat{\sigma}^2$ 无关的项，重新整理得到
$\boxed{ \begin{aligned} \mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) = -\frac{1}{2} \log\Big\vert \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big\vert -\frac{1}{2} \mathbf{t}^{\rm T} \Big( \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big)^{-1} \mathbf{t} \end{aligned} }$
其中第一项（注意里面的符号不是绝对值而是矩阵行列式的 $\det$），利用 The Matrix Determinant Lemma (MDL)
$\boxed{ \textcolor{purple}{ \Big\vert \mathbf A+\mathbf{BC} \Big\vert= \Big\vert \mathbf A \Big\vert \cdot \Big\vert \mathbf I +\mathbf{A}^{-1}\mathbf{BC} \Big\vert = \Big\vert \mathbf A \Big\vert \cdot \Big\vert \mathbf I + \mathbf{C A}^{-1}\mathbf B \Big\vert }}$
因此，可推导出
$\begin{aligned} \Big\vert \mathbf{\Lambda}^{-1}_{\alpha} + \sigma^{-2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi} \Big\vert &= \Big\vert \sigma^{-2}\mathbf I (\sigma^{2}\mathbf{\Lambda}^{-1}_{\alpha} + \mathbf{\Phi}^{\rm T}\mathbf{\Phi} ) \Big\vert \\ &= \Big\vert \sigma^{-2}\mathbf I\Big\vert \cdot \Big\vert \sigma^{2}\mathbf{\Lambda}^{-1}_{\alpha} + \mathbf{\Phi}^{\rm T}\mathbf{\Phi} \Big\vert \\ \Big\vert \sigma^{2}\mathbf I\Big\vert \Big\vert \mathbf{\Lambda}^{-1}_{\alpha} + \sigma^{-2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi} \Big\vert &= \Big\vert \sigma^{2}\mathbf{\Lambda}^{-1}_{\alpha} + \mathbf{\Phi}^{\rm T}\mathbf{\Phi} \Big\vert \\ &= \Big\vert \sigma^{2}\mathbf{\Lambda}^{-1}_{\alpha} \Big\vert \cdot \Big\vert \mathbf{I}+ \sigma^{-2} \mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big\vert \\ &= \Big\vert \mathbf{\Lambda}^{-1}_{\alpha} \Big\vert \Big\vert \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big\vert \end{aligned}$

第一项结合 $\mathbf \Sigma_w^{-1} = \frac{1}{\sigma^2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\mathbf{\Lambda}_{\alpha}^{-1}$ 可表示为
$\begin{aligned} -\frac{1}{2} \log\Big\vert \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big\vert &=-\frac{1}{2} \log \bigg\{ \frac{\Big\vert \sigma^{2}\mathbf I\Big\vert \cdot \Big\vert \mathbf{\Lambda}^{-1}_{\alpha} + \sigma^{-2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi} \Big\vert }{\Big\vert \mathbf{\Lambda}^{-1}_{\alpha} \Big\vert } \bigg\} \\ &= \frac{1}{2} \bigg\{\log \Big\vert \mathbf{\Lambda}^{-1}_{\alpha} \Big\vert- \log \Big\vert \sigma^{2}\mathbf I \Big\vert -\log \Big\vert \mathbf{\Lambda}^{-1}_{\alpha} + \sigma^{-2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi} \Big\vert \bigg\}\\ &= \frac{1}{2}\bigg( \sum_{i=1}^{M} \log \alpha_i -N\log \sigma^2 + \log \Big\vert \mathbf\Sigma_w \Big\vert \bigg) \end{aligned}$

下面分析第二项，利用矩阵求逆引理（也称作 Woodbury matrix identity，also known as the binomial inverse theorem）以及 $\bm\mu_w = \sigma^{-2} \mathbf \Sigma_w \mathbf{\Phi}^{\rm T}\mathbf t$，可得
$\begin{aligned} &-\frac{1}{2} \mathbf{t}^{\rm T} \Big( \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big)^{-1} \mathbf{t} \\ =& -\frac{1}{2} \mathbf{t}^{\rm T} \Big( \sigma^{-2} \mathbf{I} -\sigma^{-2} \mathbf{\Phi}\left[ \mathbf{\Lambda}^{-1}_{\alpha}+\sigma^{-2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi} \right]^{-1} \mathbf{\Phi}^{\rm T} \sigma^{-2} \Big) \mathbf{t} \\ =& -\frac{\sigma^{-2}}{2} \mathbf{t}^{\rm T} \Big( \mathbf{I} - \mathbf{\Phi} \mathbf\Sigma_w \mathbf{\Phi}^{\rm T} \sigma^{-2} \Big) \mathbf{t} = -\frac{\sigma^{-2}}{2} \Big( \mathbf{t}^{\rm T}\mathbf{t} - \sigma^{-2} \mathbf{t}^{\rm T} \mathbf{\Phi} \mathbf\Sigma_w \mathbf{\Phi}^{\rm T} \mathbf{t} \Big) \\ =& -\frac{1}{2} \sigma^{-2} \Big( \mathbf{t}^{\rm T}\mathbf{t} - \mathbf{t}^{\rm T} \mathbf{\Phi}\bm \mu_w\Big) \\ =& -\frac{1}{2} \sigma^{-2} \Big( \Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 + \bm \mu_w^{\rm T}\mathbf{\Phi}^{\rm T} \mathbf{t} -\bm\mu_w^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}\bm\mu_w \Big) \\ =& -\frac{1}{2} \Big( \sigma^{-2}\Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 + \sigma^{-2}\bm \mu_w^{\rm T}\mathbf{\Phi}^{\rm T} \mathbf{t} - \sigma^{-2}\bm\mu_w^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}\bm\mu_w \Big) \\ =& -\frac{1}{2} \Big( \sigma^{-2}\Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 + \bm \mu_w^{\rm T}\mathbf\Sigma^{-1}_w \bm \mu_w - \sigma^{-2}\bm\mu_w^{\rm T}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}\bm\mu_w \Big) \\ =& -\frac{1}{2} \Big( \sigma^{-2}\Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 + \bm \mu_w^{\rm T} (\mathbf\Sigma^{-1}_w - \sigma^{-2} \mathbf{\Phi}^{\rm T}\mathbf{\Phi} )\bm \mu_w \Big) \\ =& -\frac{1}{2} \Big( \sigma^{-2}\Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 + \bm \mu_w^{\rm T} \mathbf{\Lambda}_{\alpha}^{-1} \bm \mu_w \Big) \\ \end{aligned}$

不行了，要推导吐了。允许我加个表情 ???。

现在两项都已经整理好了，重新回到对数似然函数这块：

$\begin{aligned} \mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) &= -\frac{1}{2} \log\Big\vert \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big\vert -\frac{1}{2} \mathbf{t}^{\rm T} \Big( \sigma^2 \mathbf{I}+\mathbf{\Phi}\mathbf{\Lambda}_{\alpha}\mathbf{\Phi}^{\rm T} \Big)^{-1} \mathbf{t} \\ &= \frac{1}{2}\bigg( \sum_{i=1}^{M} \log \alpha_i -N\log \sigma^2 + \log \Big\vert \mathbf\Sigma_w \Big\vert \bigg) -\frac{1}{2} \Big( \sigma^{-2}\Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 + \bm \mu_w^{\rm T} \mathbf{\Lambda}_{\alpha}^{-1} \bm \mu_w \Big) \end{aligned}$
下面进入不断更新求导的过程。首先针对 $\bm \alpha$ 考虑，令 $\log \alpha_i =p_i$，则有 $e^{p_i}=\alpha_i$ 以及 $\frac{\partial \alpha_i}{\partial p_i}=e^{p_i}=\alpha_i$。
因此我们令
$\begin{aligned} \frac{\partial \mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) }{\partial p_i} &= 0 \end{aligned}$
逐个分析导数：
$\begin{aligned} \mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) &= \frac{1}{2}\bigg( \sum_{i=1}^{M} \log \alpha_i -N\log \sigma^2 + \log \Big\vert \mathbf\Sigma_w \Big\vert - \sigma^{-2}\Vert \mathbf t- \mathbf{\Phi}\bm\mu_w\Vert^2 - \bm \mu_w^{\rm T} \mathbf{\Lambda}_{\alpha}^{-1} \bm \mu_w \bigg) \\ \frac{\partial \log \Big\vert \mathbf\Sigma_w \Big\vert}{\partial p_i} &= -\frac{\partial \log \Big\vert \mathbf\Sigma^{-1}_w \Big\vert}{\partial p_i} \end{aligned}$
接着利用数学分析的定理：
当矩阵 $\mathbf{A}(t)$ 可逆时，有
$\frac{\text d }{\text d t}\log \det \mathbf{A} = \text{tr} \left( \mathbf{A}^{-1} \frac{\text d \mathbf{A}}{\text d t} \right)$
这是一个特别有用的公式，在很多数学分支中都会用到。该定理可以在 PRML 书中的附录找到。
因为 $\mathbf{\Lambda}_{\alpha}=\text{diag}([\alpha_1^{-1},\cdots,\alpha_M^{-1}])$，则 $\mathbf{\Lambda}^{-1}_{\alpha}=\text{diag}([\alpha_1,\cdots,\alpha_M])$。
$\begin{aligned} \frac{\partial \log \Big\vert \mathbf\Sigma_w \Big\vert}{\partial p_i} &= -\frac{\partial \log \Big\vert \mathbf\Sigma^{-1}_w \Big\vert}{\partial p_i} \\ &=- \text{tr} \left( \mathbf\Sigma_w \frac{\partial \mathbf\Sigma^{-1}_w}{\partial p_i} \right) \\ &=- \text{tr} \left( \mathbf\Sigma_w \frac{\partial \mathbf{\Lambda}^{-1}_{\alpha}}{\partial p_i} \right) \\ &=- [\mathbf\Sigma_w]_{i,i} \frac{\partial {\alpha}_i}{\partial p_i} =- [\mathbf\Sigma_w]_{i,i} \cdot \alpha_i \end{aligned}$

写到这里，我不得不吐槽一句，RVM/SBL 涉及的数学还真特么的多，多到不忍直视 ?。

然后还有
$\begin{aligned} \frac{\partial \bm \mu_w^{\rm T} \mathbf{\Lambda}_{\alpha}^{-1} \bm \mu_w}{\partial p_i} &=\mu_i^2\alpha_i \end{aligned}$
则最终可以得到
$\begin{aligned} \frac{\partial \mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) }{\partial p_i} &= 1- [\mathbf\Sigma_w]_{i,i} \cdot \alpha_i - \mu_i^2\alpha_i =0 \end{aligned}$
ps：在这里不知道你有没有疑问，明明 $\bm \mu$ 是 $\mathbf \Sigma$ 的函数，为什么在这里将 $\bm \mu$ 视作与 $\alpha_i$ 无关的变量呢？这个问题待定吧。同时在这个假设基础上，我们令
$\begin{aligned} 1- [\mathbf\Sigma_w]_{i,i} \cdot \alpha_i =\gamma_i \rightarrow [\mathbf\Sigma_w]_{i,i} = \frac{1-\gamma_i}{\alpha_i} \\ \\ 1- [\mathbf\Sigma_w]_{i,i} \cdot \alpha_i - \mu_i^2\alpha_i =0 \rightarrow \gamma_i = \mu_i^2\alpha_i \end{aligned}$
最终更新过程为

$\boxed{ \begin{aligned} \alpha_i^{\text{new}} = \frac{\gamma_i}{\mu_i^2} \end{aligned} }$

---

再针对 $\sigma^2$ 求导，令 $\log \sigma^{-2}= q$，则 $\frac{\partial \sigma^{-2}}{\partial q}=\sigma^{-2}$。注意 $\mathbf \Sigma_w^{-1} = {\sigma^{-2}}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\mathbf{\Lambda}_{\alpha}^{-1}$，可以得到
$\begin{aligned} \frac{\mathcal L( \mathbf t \vert \sigma^2, \boldsymbol \alpha) }{\partial q} &= N-\frac{\partial \log \Big\vert \mathbf\Sigma^{-1}_w \Big\vert}{\partial q}- \sigma^{-2}\Vert \mathbf t - \mathbf{\Phi}\bm\mu_w\Vert^2 \\ &=N-\text{tr} \left(\sigma^{-2} \mathbf\Sigma_w \mathbf{\Phi}^{\rm T}\mathbf{\Phi} \right)- \sigma^{-2}\Vert \mathbf t - \mathbf{\Phi}\bm\mu_w\Vert^2 \\ &=N- \sigma^{-2}\Vert \mathbf t - \mathbf{\Phi}\bm\mu_w\Vert^2 -\text{tr} \bigg( \mathbf\Sigma_w (\mathbf\Sigma_w^{-1}-\mathbf{\Lambda}_{\alpha}^{-1}) \bigg) \\ &=N- \sigma^{-2}\Vert \mathbf t - \mathbf{\Phi}\bm\mu_w\Vert^2 - \sum_i \gamma_i =0 \end{aligned}$

则更新过程为
$\boxed{ \begin{aligned} (\sigma^2)^{\text{new}} = \frac{\Vert \mathbf t - \mathbf{\Phi}\bm\mu_w\Vert^2}{N-\sum_i \gamma_i} \end{aligned} }$

首先随机初始化两个待估参数 $\alpha, \sigma^2$，随即得到
$\begin{aligned} \mathbf \Sigma_w^{-1} &= \frac{1}{\sigma^2}\mathbf{\Phi}^{\rm T}\mathbf{\Phi}+\mathbf{\Lambda}_{\alpha}^{-1} \\ \bm\mu_w &= \sigma^{-2} \mathbf \Sigma_w \mathbf{\Phi}^{\rm T}\mathbf t \end{aligned}$
总结过程为
$\begin{aligned} \alpha_i^{\text{new}} &= \frac{\gamma_i}{\mu_i^2} \\ (\sigma^2)^{\text{new}} &= \frac{\Vert \mathbf t - \mathbf{\Phi}\bm\mu_w\Vert^2}{N-\sum_i \gamma_i} \\ \gamma_i &= 1- [\mathbf\Sigma_w]_{i,i} \cdot \alpha_i \end{aligned}$

这意味着我们可以通过学习算法获得超参数 $\alpha, \sigma^2$，而不需要通过交叉验证来确定。在足够多的更新后，大部分的 $\alpha_i \rightarrow \infty$，即对应的 $w_i \rightarrow 0$。其余的 $\alpha_i$ 会稳定趋近有限值，与之对应的样本 $\mathbf x_i$ 就被称为 relevance vector。

至此所有公式推导完毕，开始实践吧。