博客简介
本博客是大二下学期CSAPP课程的第六次小班讨论课内容,本博客记录如何用gprof剖析程序性能,以及循环展开极限和常见的优化方法
gprof简介
GNU gprof 是一款linux平台上的程序分析软件(unix也有prof)。借助gprof可以获得C/C++程序运行期间的统计数据,例如每个函数耗费的时间,函数被调用的次数以及各个函数相互之间的调用关系。gprof可以帮助我们找到程序运行的瓶颈,对占据大量CPU时间的函数进行调优。
gprof统计的只是用户态CPU的占用时间,不包括内核态的CPU时间。gprof对I/O瓶颈无能为力,耗时甚久的I/O操作很可能只占据极少的CPU时间。其使用方法步骤如下:
- 使用编译标志-pg编译代码。
- 运行程序生成剖析数据。
- 运行gprof分析剖析数据,得到可视结果。
- 举例
linux:>gcc -g -pg test.c -o test
linux:>./test
linux:>gprof -b test -gmon.out
指令参数列表:
| 参数 | function | example |
|---|---|---|
| -a | 屏蔽静态私有函数信息 | gprof -a test gmon.out > analysis.txt |
| -b | gprof -a test gmon.out > analysis.txt | gprof -b test gmon.out > analysis.txt |
| -p(function) | 只打印function函数信息 | gprof -pa test gmon.out > analysis.txt |
| -P | 屏蔽flat profile信息 | gprof -P test gmon.out > analysis.txt |
| -q | 只打印call graph信息 | gprof -q test gmon.out > analysis.txt |
| -q(function) | 只打印function函数的call graph信息 | gprof -qa test gmon.out > analysis.txt |
| -Q | 屏蔽call graph信息 | gprof -Q test gmon.out > analysis.txt |
题 1:有如下代码:
sum = 0;
for (i = 0; i < length; i++)
sum += x[i] * y[i];
利用在第 5 章学习的相关技术,分析可能影响性能的部分,并尝试进行性能提升。要求: (1)利用反汇编技术,与 gcc 汇编器优化进行比较;
- 在此之前先得到汇编文件或反汇编文件,执行指令:
Linux:>gcc -o sum0 sum.c 生成可执行文件
Linux:> objdump -D sum0 >sum0.txt 将sum0反汇编
Linux:> gcc -S -O1 sum.c -o sum1.s 将.c文件一级优化
Linux:> gcc -S -O2 sum.c -o sum2.s 将.c文件二级优化
- 得到文件如下:
① Sum0,反汇编源码分析
80483b4: 55 push %ebp
80483b5: 89 e5 mov %esp,%ebp
80483b7: 83 ec 10 sub $0x10,%esp
80483ba: c7 45 f0 00 00 00 00 movl $0x0,-0x10(%ebp) //初始化,存放乘积和sum
80483c1: c7 45 f4 00 00 00 00 movl $0x0,-0xc(%ebp) //初始化,带进位加法存放MM
80483c8: c7 45 fc 00 00 00 00 movl $0x0,-0x4(%ebp) //初始化,计数地址
80483cf: eb 28 jmp 80483f9 <sum+0x45>
80483d1: 8b 45 fc mov -0x4(%ebp),%eax //循环开始将 -0x4(%ebp)的值存入eax
80483d4: c1 e0 02 shl $0x2,%eax //eax左移2位,相当于*4,用于下标寻址
80483d7: 03 45 08 add 0x8(%ebp),%eax //将eax+0x8(%ebp),x的起始地址
80483da: 8b 10 mov (%eax),%edx //寻址,将x[i]->edx
80483dc: 8b 45 fc mov -0x4(%ebp),%eax //-0x4(%ebp)->eax
80483df: c1 e0 02 shl $0x2,%eax //eax左移2位,相当于*4,用于下标寻址
80483e2: 03 45 0c add 0xc(%ebp),%eax //将eax+0xc(%ebp),y的起始地址
80483e5: 8b 00 mov (%eax),%eax //寻址,将y[i]->edx
80483e7: 0f af c2 imul %edx,%eax //%edx,%eax相乘
80483ea: 89 c2 mov %eax,%edx //结果
80483ec: c1 fa 1f sar $0x1f,%edx //算数右移31位取符号
80483ef: 01 45 f0 add %eax,-0x10(%ebp) //将乘积加到-0x10(%ebp)
80483f2: 11 55 f4 adc %edx,-0xc(%ebp)
//带进位加法指令 ADC(Addition Carry),ADC指令的引入主要是为了实现多字节的运算
//当进行32位以上运算时要求低位字节相加,而高位字节再相加时就要考虑低位相加的进位
//即CF,这时就要用到ADC指令。ADC OPRD1,OPRD2,OPRD1<--OPRD1 + OPRD2 + CF
80483f5: 83 45 fc 01 addl $0x1,-0x4(%ebp) //计数
80483f9: 8b 45 fc mov -0x4(%ebp),%eax //计数地址->eax,eax为下标
80483fc: 3b 45 10 cmp 0x10(%ebp),%eax //比较n和eax
80483ff: 7c d0 jl 80483d1 <sum+0x1d>
8048401: 8b 45 f0 mov -0x10(%ebp),%eax
8048404: 8b 55 f4 mov -0xc(%ebp),%edx
8048407: c9 leave
8048408: c3 ret
② sum1一级优化O1汇编指令分析:
movl 20(%esp), %edi //x[]
movl 24(%esp), %ebp //y[]
movl $0, %ecx //乘积之和sum->ecx
movl $0, %ebx
cmpl $0, 28(%esp) //n
jle .L2
movl $0, %esi //计数下标
.L3:
movl (%edi,%esi,4), %eax //x[i]->eax
imull 0(%ebp,%esi,4), %eax //eax*y[i]
movl %eax, %edx
sarl $31, %edx
addl %eax, %ecx //将低32位的乘积存放在ecx
adcl %edx, %ebx //带进位加法处理edx
addl $1, %esi //下标加1
cmpl 28(%esp), %esi
jne .L3
.L2:
③ sum2二级优化O2汇编指令分析:
xorl %ecx, %ecx //ecx异或清零
pushl %edi
.cfi_def_cfa_offset 12
.cfi_offset 7, -12
pushl %esi
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
pushl %ebx
.cfi_def_cfa_offset 20
.cfi_offset 3, -20
movl 28(%esp), %eax //n,首先比较0和n,如果n为零就直接返回
xorl %ebx, %ebx //清零ebx
movl 20(%esp), %ebp //ebp存储x[]起始地址
movl 24(%esp), %edi //edi存储y[]起始地址
testl %eax, %eax //判断eax是否为0
jle .L2
xorl %esi, %esi //清零
.p2align 4,,7
.p2align 3
.L3:
movl 0(%ebp,%esi,4), %eax //寻址x[i]
imull (%edi,%esi,4), %eax //计算eax*y[i]
movl %eax, %edx
sarl $31, %edx //取符号
addl %eax, %ecx //将eax加到ecx
adcl %edx, %ebx //带进位加法处理edx
addl $1, %esi //下标++
cmpl 28(%esp), %esi
jne .L3
.L2:
-
比较未优化,O1级优化,O2优化的差异:
-
① 对于未优化的级别程序,可以发现sum,计数值i,以及高32位的值都存放在内存中,另外两个数组的起始地址也存放在内存中。显然这样的程序没有合理使用寄存器,二是访问内存,因此性能不强。
-
②O1级别的优化,编译器在不花费过多编译时间的同时, 试图生成更快更小的代码,另外以上的sum,计数值i,以及高32位的值,两个数组的起始地址都存放到了寄存器中,最大化的使用了寄存器,减少了内存的访问,因而提高了效率。
-
③O2级别的优化,代码长度和O1近似,而且同样将sum,计数值i,以及高32位的值,两个数组的起始地址都存放到了寄存器中合理引用了寄存器。除此之外还有一个比较重要的是,程序在开始之前清零使用了xorl异或指令而不是传送指令,xor指令比mov指令占用CPU周期更小。另外还有一个比较有特点的是程序在循环之前对eax和0进行了比较,如果eax=0那么说明n=0就无需执行循环了,程序也是这么做的,显然这是一个很聪明的优化方式。
(2)比较循环展开次数对性能的影响,如展开 2 次和 3 次,展开次数越多越好吗?
这里我的思路是构造程序,对程序进行了1~18次展开,用C/C++性能测试工具 GNU gprof测试函数的执行时间,并且统计函数的执行结果。下面是分析步骤:
- ① 测试程序:程序重文件按中读取100000组数据,测试每一组函数时将会将这个函数执行10000次以将各组之间的优化差距扩大,部分程序如下:
void input(int x[],int y[],const char*s,int n)
{
FILE* fp;
fp=fopen(s,"r");
int i=0,z;
while(fscanf(fp,"%d",&z)!=-1&&i<n)
{
x[i]=z;
x[i++]=z;
}
fclose(fp);
printf("%d\n",i);
}
long long sum1(int x[],int y[],int n)
{
long long sum=0;
int i;
for(i=0;i<n;i++)
{
sum+=x[i]*y[i];
}
return sum;
}
void testSum1(int x[],int y[],int n){
int i=0;
for(i=0;i<10000;i++) sum1(x,y,n);
}
long long sum2(int x[],int y[],int n)//循环展开2
{
long long sum=0;
int i,limit=n-1;
for(i=0;i<limit;i+=2)
{
sum+=x[i]*y[i]+x[i+1]*y[i+1];
}
for(;i<n;i++)
{
sum+=x[i]*y[i];
}
return sum;
}
void testSum2(int x[],int y[],int n){
int i=0;
for(i=0;i<10000;i++) sum2(x,y,n);
}
- ② gproft 测试性能,执行指令:
Linux:> gcc -g -pg sum.c -o sum 使用编译标志-pg编译代码
Linux:>./sum 运行程序生成剖析数据
Linux:> gprof -b sum gmon.out 运行剖析问文件得到可视化数据



- ③ 将得到的数据进行数据分析,绘制成折线:

- ④ 结果分析:
我们发现随着循环次数的展开,程序运行的时间呈现递减趋势,也就是说程序性能逐渐增强。但是随着循环展开次数继续增加,程序的性能逐渐平缓,最后几乎水平甚至还会有上升。由Amdahl 定律也可知,S=1/(1-a)+a/k,就算k->无穷大,程序还受到a之外的因素制约。 - ⑤结论:展开次数并不是越多越好,随着展开次数的增加,程序性能逐渐增强,最后趋于平缓,此时制约程序性能的将不再是循环的展开次数,二是受限于其他因素。但是程序的可读性会因此变差,所以需要程序员权衡。
(3)其他可能优化的方法?
对于其他程序优化的方法,这里提供了以下思路:
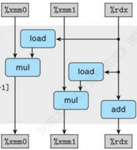
- ① 考虑提高并行性:我们可以绘制关键路径,发现程序是完全串行进行每次sum求和都要等到上一次乘法指令执行完毕,可以引入新变量acc0和acc1, (多个累积变量)分配到不同 寄存器中。以下是一个2路并行实现样例:
long long sums(int x[],int y[],int n)
{
long long sum=0,acc0,acc1;
int i,limit=n-1;
for(i=0;i<limit;i++)
{
acc0+=x[i]*y[i];
acc1+=x[i+1]*y[i+1];
}
for(;i<n;i++)
sum+=x[i]*y[i];
sum+=acc0+acc1;
return sum;
}
- ② 考虑重新结合变换:
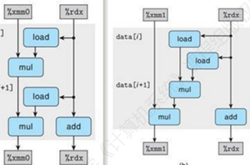
load mul顺序执行,必须等到第一个 load mu执行完成以后才能进行第二次load和lum操作。如果采用重新结合变换,每次迭代的第一个乘法不需要等待前一次迭代的累积值就可以执行(减少操作的数量)。一个实现样例如下:
long long sums2(int x[],int y[],int n)
{
long long sum=0;
int i,limit=n-1;
for(i=0;i<limit;i+=2)
{
sum=sum+(x[i]*y[i]+x[i+1]*y[i+1]);
}
for(;i<n;i++)
{
sum+=x[i]*y[i];
}
return sum;
}
- ③ 用临时变量存储x[]的一行数来提高cache命中率
如果说不优化命中率,那么每次访问x[i]和访问y[i]都对应到cache2的同一行,那么读取y[i]的时候将会驱逐x[i],那么命中率为0,不命中率很高很高。因此我们可以考虑用临时变量存储x[]的一组连续的数据,这样一来在访问y[i]的时候只有第一次发生驱逐,因此用临时变量存储x[]的一行数来提高cache命中率,以下是一个实现方案:
long long sums3Block(int x[],int y[],int n)
{
long long sum=0;
int i,j,limit=n-7,x1,x2,x3,x4,x5,x6,x7,x8;
for(i=0;i<limit;i+=8)
{
x1=x[i],x2=x[i+1],x3=x[i+2],x4=x[i+3],x5=x[i+4],x6=x[i+5],x7=x[i+6],x8=x[i+7];
sum+=x1*y[i]+x2*y[i+1]+x3*y[i+2]+x4*y[i+3]+x5*y[i+4]+x6*y[i+5]+x7*y[i+6]+x8*y[i+7];
}
for(;i<n;i++)
{
sum+=x[i]*y[i];
}
return sum;
}
题二:
将一个有向图 g 转换成其相应的无向图 g’,无向图中有一条 从顶点 u 到顶点 v 的边,当且仅当原有向图中有一条 u 到 v 或者 v 到 u 的边。有向图 g 由如下的它的邻接矩阵 G 表示:如果 N 是 g 中顶 点的数量,那么 G 是一个 N*N 的矩阵,它的元素是全 0 或者全 1。 设若 g 的顶点命名为 v0,v1,……,vN-1。那么如果有一条从 vi 到 vj 的边,则 G[i][j]值为 1,否则为 0。注意:邻接矩阵对角线上的元 素总是 1,而无向图的邻接矩阵是对称的。仅用一个循环实现这段代 码:
请结合第 5 章~ 6 章所学的内容,尝试设计一个运行得尽可能快的函数。
① 基础线性化:首先我处理的是如何只用一层循环处理矩阵,可以对len取余dim就能得到j,len除以dim就能得到i,利用这个关系可以将2层循环降为1层循环,除此之外,为了防止重复计算可以在执行或操作之前判断i和j的大小,如果i<j,那么就可以不处理了,左下半边已经处理过了,所以可以避免重复计算:
void graph0(int* G,int dim)
{
int k,limit=dim*dim;
for(k=0;k<limit;k++)
{
int i=k/dim,j=k%dim;
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
}
}

但是改进的效果不尽人意,6.71*0.01s的运行时间比原始函数还要差。
② 循环4次展开
最先想到是循环展开技术,可以将循环展开4次,避免重复的计算,减少开销,因为循环展开最后一行只需要处理一个元素,所以需不需要像教材中那样处理dim-2,dim-1,dim这几个剩下的元素:
void graph1(int* G,int dim)
{
int k,limit=dim*dim-3;
for(k=0;k<limit;k+=4)
{
int i=k/dim,j=k%dim;
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
i=(k+1)/dim,j=(k+1)%dim;
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
i=(k+2)/dim,j=(k+2)%dim;
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
i=(k+3)/dim,j=(k+3)%dim;
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
}
}

经验证,运行时间从6.71减少到了6.36,效果微乎其微。
③ 循环展开+条件判断避免除法和取余:
直接循环展开的优化结果似乎不尽人意,运行时间从6.71减少到了6.36,效果微乎其微,仔细一想乘法操作和取余操作可以通对i和j进行判断,如果j==dim那么更新i++,j=0,从而避免除法和取余操作:
void graph2(int* G,int dim)
{
int k,limit=dim*dim-3,i=0,j=0;
for(k=0;k<limit;k+=4)
{
if(j==dim)
{
j=0;
i++;
}
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
j++;
i--;
if(j==dim)
{
j=0;
i++;
}
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
j++;
i--;
if(j==dim)
{
j=0;
i++;
}
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
j++;
i--;
if(j==dim)
{
j=0;
i++;
}
if(i>=j)
{
int temp=G[j*dim+i]||G[i*dim+j];
G[j*dim+i]=temp;
G[i*dim+j]=temp;
}
}
}

经验证,运行时间减小到了1.45,优化效果可观。
④ 4路并行,并行处理我使用了i0,i1,i2,i3,j1,j2,j3,j4共4组临时变量来存储下标,同样的用ifelse来进行判断,避免取余和出发计算,注意不要使用加法的迭代,这样程序会出现读写相关!所以说每个变量都是独立的,4路并行,加法操作可以独立进行,从而达到加速的目的,以下是实现代码:
void graph3(int* G,int dim)
{
int k,limit=dim*dim-3;
int i0=0,j0=0;
for(k=0;k<limit;k+=4)
{
int i1,i2,i3,j1,j2,j3;
if(j0==dim-3)
{
i1=i0;
j1=j0+1;
i2=i0;
j2=j0+2;
i3=i0+1;
j3=0;
}
if(j0==dim-2)
{
i1=i0;
j1=j0+1;
i2=i0+1;
j2=0;
i3=i0+1;
j3=1;
}
if(j0==dim-1)
{
i1=i0+1;
j1=0;
i2=i0+1;
j2=1;
i3=i0+1;
j3=2;
}
else
{
i1=i0;
j1=j0+1;
i2=i0;
j2=j0+2;
i3=i0;
j3=j0+3;
}
if(i0>=j0)
{
int temp0=G[j0*dim+i0]||G[i0*dim+j0];
G[j0*dim+i0]=temp0;
G[i0*dim+j0]=temp0;
}
if(i1>=j1)
{
int temp1=G[j1*dim+i1]||G[i1*dim+j1];
G[j1*dim+i1]=temp1;
G[i1*dim+j1]=temp1;
}
if(i2>=j2)
{
int temp2=G[j2*dim+i2]||G[i2*dim+j2];
G[j2*dim+i2]=temp2;
G[i2*dim+j2]=temp2;
}
if(i3>=j3)
{
int temp3=G[j3*dim+i3]||G[i3*dim+j3];
G[j3*dim+i3]=temp3;
G[i3*dim+j3]=temp3;
}
j0+=4;
if(j0>=dim)
{
j0=0;
i0+=1;
}
}
}

经验证,4路循环展开+4路并行+避免除法取余可以将程序性能优化到1.28,性能提高近3倍。
⑤ 结论:这段代码可以通过取模和除法操作线性化去掉一层循环,优化则考虑计算矩阵左上边部分,循环展开和多路并行的操作,最后综合起来程序性能优化后运行时间为1.28*0.01s,性能优化3倍左右。
⑥ 分块处理:
- 分块处理可以提高空间局部性,增加cache的命中率,举一个例子,我们假设cache的规模是<s=4,E=1,b=4>,那么如果没有对程序优化可以得到如下的命中结果。

其描述的是读取G[i]右上角部分和存储G[j]的过程左下角部分,其中存储G[j]的不命中率为%100!而读取G[i]的不命中率为25%。 - 现在我们对矩阵进行分块,也就是说每4*4为一块,这样一来每次存储B的第一个数据会将B~B+3共四个数据存储在cache中,因此可以被顺利命中,这样一来存储和读取G[i],G[j]的不命中率都降低到了25%:

- 实现样例,以下是我的一条4*4分块代码:
void graphCache(int* G,int dim)
{
int limit=dim*dim-3,bord=dim/4;
int i=0,j=0,k=0,m=0,n=0;//m表示块内部的第m行,n表示第n个块,模拟循环
for(i=0;i<limit;)
{
//处理4行
G[i]=G[i]||G[j];i++;j+=dim;
G[i]=G[i]||G[j];i++;j+=dim;
G[i]=G[i]||G[j];i++;j+=dim;
G[i]=G[i]||G[j];
m++;
if(m==4)//处理新块
{
m=0;
n++;
if(n==bord)//换行
{
n=0;
i++;
//j+=1-dim*dim;
j+=1+dim-dim*dim;
}
else //换块
{
i-=3*dim+1;
j+=dim-3;
}
}
else{//块内换行
i+=dim-3;
j+=1-3*dim;
}
}
}
结果分析:
采用分块技术可以将不命中率降低到25%左右,从而提高代码执行效率,经过测试执行时间减小到了2.65*0.01s,相比于源码6.71的时间,执行效率提高了2.53倍。
结论:
⑦ 在无向图转换的例子中,我采用了4种优化方法:循环4次展开,循环展开+条件判断避免除法和取余:4路并行,分块处理,优化后的执行时间分别为:6.36,1.45,1.28,2.65,循环展开+条件判断避免除法和取余优化效果最佳。

