1.Assume
x
(
t
)
↔
F
T
X
(
j
ω
)
x(t) \xleftrightarrow[]{FT}X(j\omega)
x ( t ) F T
X ( j ω )
Can
e
j
a
ω
X
(
ω
)
e^{ja \omega}X(\omega)
e j a ω X ( ω )
Can
X
(
j
ω
)
X(j\omega)
X ( j ω )
Can
∫
−
∞
∞
ω
X
(
j
ω
)
d
ω
\int_{-\infty}^\infty{\omega X(j \omega) d\omega}
∫ − ∞ ∞ ω X ( j ω ) d ω
Can
R
e
(
X
(
j
ω
)
)
=
0
Re ({{{X(j\omega)}}})=0
R e ( X ( j ω ) ) = 0
I
m
(
X
(
j
ω
)
)
=
0
Im(X{(j\omega)})=0
I m ( X ( j ω ) ) = 0
Solve:
x
(
t
)
↔
F
T
X
(
j
ω
)
(1-1)
x(t) \xleftrightarrow[]{FT}X(j\omega) \tag{1-1}
x ( t ) F T
X ( j ω ) ( 1 - 1 )
x
(
t
+
a
)
↔
F
T
e
j
a
ω
X
(
ω
)
=
X
1
(
j
ω
)
(1-2)
x(t+a) \xleftrightarrow[]{FT} e^{ja \omega}X(\omega) =X_{1}(j\omega)\tag{1-2}
x ( t + a ) F T
e j a ω X ( ω ) = X 1 ( j ω ) ( 1 - 2 )
x
(
t
)
↔
F
T
X
(
j
ω
)
(1-3)
x(t) \xleftrightarrow[]{FT}X(j\omega) \tag{1-3}
x ( t ) F T
X ( j ω ) ( 1 - 3 )
x
(
−
t
)
↔
F
T
X
(
−
j
ω
)
(1-4)
x(-t) \xleftrightarrow[]{FT}X(-j\omega) \tag{1-4}
x ( − t ) F T
X ( − j ω ) ( 1 - 4 )
x
∗
(
t
)
↔
F
T
X
∗
(
−
j
ω
)
(1-5)
x^{*}(t) \xleftrightarrow[]{FT}X^{*}(-j\omega) \tag{1-5}
x ∗ ( t ) F T
X ∗ ( − j ω ) ( 1 - 5 )
X
1
(
j
ω
)
X_{1}(j\omega)
X 1 ( j ω )
X
∗
(
j
ω
)
=
X
(
j
ω
)
(1-6)
X^{*}(j\omega)=X(j\omega) \tag{1-6}
X ∗ ( j ω ) = X ( j ω ) ( 1 - 6 )
x
(
t
+
a
)
=
x
∗
(
t
+
a
)
(1-7)
x(t+a)=x^{*}(t+a) \tag{1-7}
x ( t + a ) = x ∗ ( t + a ) ( 1 - 7 )
x
(
t
+
a
)
=
x
(
−
t
+
a
)
(1-8)
x(t+a)=x(-t+a) \tag{1-8}
x ( t + a ) = x ( − t + a ) ( 1 - 8 )
x
(
t
)
x(t)
x ( t )
t
=
a
t=a
t = a
2).根据对偶性,若:
x
(
t
)
↔
F
T
X
(
j
ω
)
(2-1)
x(t) \xleftrightarrow[]{FT}X(j\omega) \tag{2-1}
x ( t ) F T
X ( j ω ) ( 2 - 1 )
X
(
t
)
↔
F
T
2
π
x
(
−
j
ω
)
(2-2)
X(t) \xleftrightarrow[]{FT}2\pi x(-j\omega) \tag{2-2}
X ( t ) F T
2 π x ( − j ω ) ( 2 - 2 )
x
(
t
)
x(t)
x ( t )
x
(
t
)
↔
F
T
X
(
j
ω
)
=
2
π
∑
k
=
−
∞
+
∞
a
k
δ
(
ω
−
k
ω
0
)
(2-3)
x(t) \xleftrightarrow[]{FT}X(j\omega) \tag{2-3}=2 \pi \sum_{k=-\infty}^{+\infty} a_{k} \delta(\omega- k\omega_{0})
x ( t ) F T
X ( j ω ) = 2 π k = − ∞ ∑ + ∞ a k δ ( ω − k ω 0 ) ( 2 - 3 )
则根据对偶性:
X
(
t
)
↔
F
T
2
π
x
(
−
j
ω
)
(2-4)
X(t) \xleftrightarrow[]{FT}2\pi x(-j\omega) \tag{2-4}
X ( t ) F T
2 π x ( − j ω ) ( 2 - 4 )
x
(
−
j
ω
)
x(-j\omega)
x ( − j ω )
综上:要求时域上的信号为冲激串形式,才可以保证其FT为周期信号 。
3). 根据IFT:
x
(
t
)
=
1
2
π
∫
−
∞
∞
e
j
ω
t
X
(
j
ω
)
d
ω
(3-1)
x(t)= \frac{1}{2\pi} \int_{-\infty}^\infty{e^{j\omega t}X(j \omega) d\omega} \tag{3-1}
x ( t ) = 2 π 1 ∫ − ∞ ∞ e j ω t X ( j ω ) d ω ( 3 - 1 )
两边同时对
t
t
t
x
′
(
t
)
=
∫
−
∞
∞
j
ω
X
(
j
ω
)
e
j
ω
t
d
ω
(3-2)
x^{'}(t)=\int_{-\infty}^\infty{j\omega X(j \omega)e^{j\omega t} d\omega} \tag{3-2}
x ′ ( t ) = ∫ − ∞ ∞ j ω X ( j ω ) e j ω t d ω ( 3 - 2 )
t
=
0
t=0
t = 0
x
′
(
0
)
=
∫
−
∞
∞
j
ω
X
(
j
ω
)
d
ω
(3-3)
x^{'}(0)=\int_{-\infty}^\infty{j\omega X(j \omega )d\omega} \tag{3-3}
x ′ ( 0 ) = ∫ − ∞ ∞ j ω X ( j ω ) d ω ( 3 - 3 ) 即为
x
′
(
t
)
=
0
x^{'}(t)=0
x ′ ( t ) = 0
4).根据共轭对称性,若要求
X
(
j
ω
)
X(j\omega)
X ( j ω )
X
(
j
ω
)
X(j\omega)
X ( j ω )
x
(
t
)
↔
F
T
X
(
j
ω
)
(3-4)
x(t) \xleftrightarrow[]{FT}X(j\omega) \tag{3-4}
x ( t ) F T
X ( j ω ) ( 3 - 4 )
x
(
−
t
)
↔
F
T
X
(
−
j
ω
)
(3-5)
x(-t) \xleftrightarrow[]{FT}X(-j\omega) \tag{3-5}
x ( − t ) F T
X ( − j ω ) ( 3 - 5 )
x
∗
(
t
)
↔
F
T
X
∗
(
−
j
ω
)
(3-6)
x^{*}(t) \xleftrightarrow[]{FT}X^{*}(-j\omega) \tag{3-6}
x ∗ ( t ) F T
X ∗ ( − j ω ) ( 3 - 6 )
现在要求:
−
X
(
j
ω
)
=
X
∗
(
j
ω
)
(3-7)
-X(j\omega)=X^{*}(j\omega) \tag{3-7}
− X ( j ω ) = X ∗ ( j ω ) ( 3 - 7 )
x
(
t
)
=
x
∗
(
t
)
(3-8)
x(t)=x^{*}(t) \tag{3-8}
x ( t ) = x ∗ ( t ) ( 3 - 8 )
x
(
t
)
=
−
x
(
−
t
)
(3-9)
x(t)=-x(-t) \tag{3-9}
x ( t ) = − x ( − t ) ( 3 - 9 )
x
(
t
)
x(t)
x ( t )
同理,对于
X
(
j
w
)
X(jw)
X ( j w )
扫描二维码关注公众号,回复:
11215022 查看本文章
X
(
j
ω
)
=
X
∗
(
j
ω
)
(3-10)
X(j\omega)=X^{*}(j\omega) \tag{3-10}
X ( j ω ) = X ∗ ( j ω ) ( 3 - 1 0 )
x
(
t
)
=
x
∗
(
t
)
(3-11)
x(t)=x^{*}(t) \tag{3-11}
x ( t ) = x ∗ ( t ) ( 3 - 1 1 )
x
(
t
)
=
x
(
−
t
)
(3-12)
x(t)=x(-t) \tag{3-12}
x ( t ) = x ( − t ) ( 3 - 1 2 )
x
(
t
)
x(t)
x ( t )
2
x
(
t
)
x(t)
x ( t )
h
(
t
)
=
∑
k
=
0
+
∞
e
−
k
T
δ
(
t
−
k
T
)
h(t)= \sum_{k=0}^{+\infty} e ^{-kT} \delta(t- kT)
h ( t ) = ∑ k = 0 + ∞ e − k T δ ( t − k T )
x
(
t
)
x(t)
x ( t )
b) When the room impulse response is modeled as
h
(
t
)
=
∑
k
=
0
K
a
k
δ
(
t
−
k
T
)
h(t)= \sum_{k=0}^{K} a_{k} \delta(t- kT)
h ( t ) = ∑ k = 0 K a k δ ( t − k T )
x
(
t
)
x(t)
x ( t )
c) Summarize time-domain and frequency-domain methods of finding the inverse system of an LTI system.
y
(
t
)
=
x
(
t
)
∗
h
(
t
)
(1-1)
y(t)=x(t)*h(t)\tag{1-1}
y ( t ) = x ( t ) ∗ h ( t ) ( 1 - 1 )
h
1
(
t
)
h_{1}(t)
h 1 ( t )
y
(
t
)
∗
h
1
(
t
)
=
x
(
t
)
(1-2)
y(t)*h_{1}(t)=x(t) \tag{1-2}
y ( t ) ∗ h 1 ( t ) = x ( t ) ( 1 - 2 )
h
(
t
)
∗
h
1
(
t
)
=
δ
(
t
)
(1-3)
h(t)*h_{1}(t)=\delta(t)\tag{1-3}
h ( t ) ∗ h 1 ( t ) = δ ( t ) ( 1 - 3 )
h
1
(
t
)
=
∑
k
=
0
+
∞
e
k
T
δ
(
t
+
k
T
)
(1-4)
h_{1}(t)= \sum_{k=0}^{+\infty} e^{kT} \delta(t+ kT) \tag{1-4}
h 1 ( t ) = k = 0 ∑ + ∞ e k T δ ( t + k T ) ( 1 - 4 )
b)
x
(
t
)
x(t)
x ( t )
h
2
(
t
)
h_{2}(t)
h 2 ( t )
h
1
(
t
)
=
∑
k
=
0
K
1
a
k
δ
(
t
+
k
T
)
(1-5)
h_{1}(t)= \sum_{k=0}^{K} \frac{1}{a_{k}} \delta(t+ kT) \tag{1-5}
h 1 ( t ) = k = 0 ∑ K a k 1 δ ( t + k T ) ( 1 - 5 )
但此时
h
2
(
t
)
h_{2}(t)
h 2 ( t )
x
(
t
)
x(t)
x ( t )
c)
h
(
t
)
h(t)
h ( t )
h
i
n
v
(
t
)
h_{inv}(t)
h i n v ( t )
h
(
t
)
∗
h
i
n
v
(
t
)
=
δ
(
t
)
(1-6)
h(t)*h_{inv}(t)=\delta(t) \tag{1-6}
h ( t ) ∗ h i n v ( t ) = δ ( t ) ( 1 - 6 )
h
(
t
)
h(t)
h ( t )
h
i
n
v
(
t
)
h_{inv}(t)
h i n v ( t )
H
(
ω
)
H
i
n
v
(
ω
)
=
1
(1-7)
H(\omega)H_{inv}(\omega)=1 \tag{1-7}
H ( ω ) H i n v ( ω ) = 1 ( 1 - 7 )
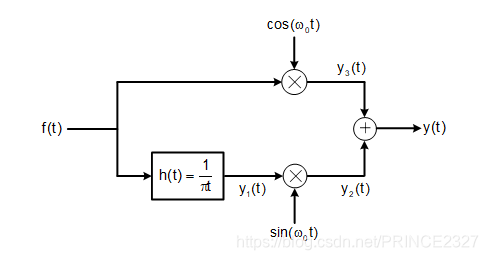
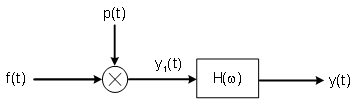
3.In communication system, single-banded modulation is an effective way to save the spectrum resource. Figure 1 shows the structure of the system that realizes the single-banded modulation.
(a)Please give an example to verify the system can realize single-banded modulation.
(b)Design a system that can recover
f
(
t
)
f(t)
f ( t )
y
(
t
)
y(t)
y ( t )
Slove:
y
3
(
t
)
=
c
o
s
(
w
0
t
)
f
(
t
)
(1-1)
y_{3}(t)=cos(w_{0}t)f(t) \tag{1-1}
y 3 ( t ) = c o s ( w 0 t ) f ( t ) ( 1 - 1 )
y
1
(
t
)
=
f
(
t
)
∗
h
(
t
)
(1-2)
y_{1}(t)=f(t)*h(t) \tag{1-2}
y 1 ( t ) = f ( t ) ∗ h ( t ) ( 1 - 2 )
y
2
(
t
)
=
s
i
n
(
w
0
t
)
y
1
(
t
)
(1-3)
y_{2}(t)=sin(w_{0}t)y_{1}(t) \tag{1-3}
y 2 ( t ) = s i n ( w 0 t ) y 1 ( t ) ( 1 - 3 )
y
(
t
)
=
y
2
(
t
)
+
y
3
(
t
)
(1-4)
y(t)=y_{2}(t)+y_{3}(t) \tag{1-4}
y ( t ) = y 2 ( t ) + y 3 ( t ) ( 1 - 4 )
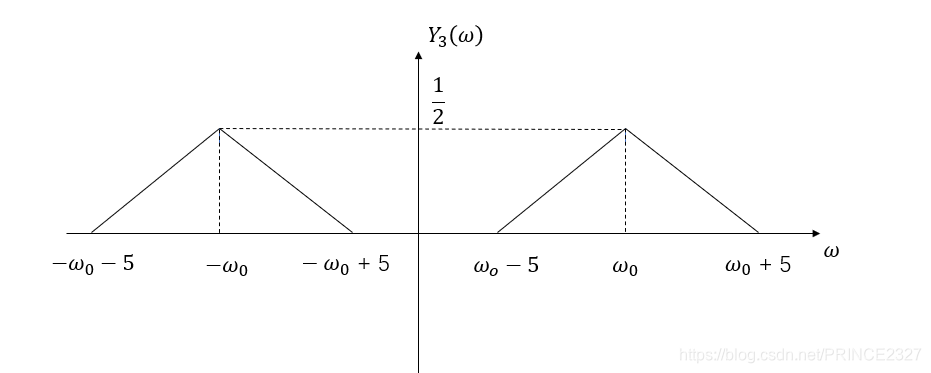
求解
Y
3
(
ω
)
Y_{3}(\omega)
Y 3 ( ω )
根据相乘性质:
Y
3
(
j
ω
)
=
1
2
π
(
π
δ
(
ω
−
ω
0
)
+
π
δ
(
ω
+
ω
0
)
)
∗
F
(
ω
)
(1-5)
Y_{3}(j \omega)=\frac{1}{2\pi}(\pi\delta(\omega-\omega_{0})+\pi\delta(\omega+\omega_{0}))*F(\omega)\tag{1-5}
Y 3 ( j ω ) = 2 π 1 ( π δ ( ω − ω 0 ) + π δ ( ω + ω 0 ) ) ∗ F ( ω ) ( 1 - 5 )
Y
3
(
j
ω
)
=
1
2
(
F
(
ω
−
ω
0
)
+
F
(
ω
+
ω
0
)
)
(1-6)
Y_{3}(j \omega)=\frac{1}{2}(F(\omega-\omega_{0})+F(\omega+\omega_{0})) \tag{1-6}
Y 3 ( j ω ) = 2 1 ( F ( ω − ω 0 ) + F ( ω + ω 0 ) ) ( 1 - 6 )
Y
1
(
j
ω
)
Y_{1}(j\omega)
Y 1 ( j ω )
Y
1
(
j
ω
)
=
H
(
j
ω
)
F
(
j
ω
)
(1-7)
Y_{1}(j\omega)=H(j\omega)F(j\omega) \tag{1-7}
Y 1 ( j ω ) = H ( j ω ) F ( j ω ) ( 1 - 7 )
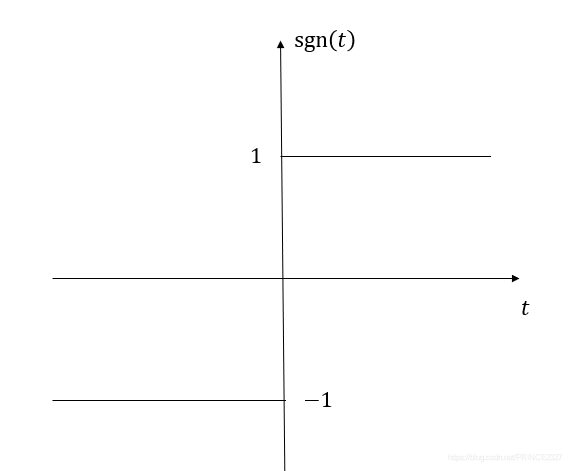
考虑如下信号:
s
g
n
(
t
)
=
2
u
(
t
)
−
1
(1-8)
sgn(t)=2u(t)-1 \tag{1-8}
s g n ( t ) = 2 u ( t ) − 1 ( 1 - 8 )
u
(
t
)
↔
F
T
1
j
ω
+
π
δ
(
ω
)
(1-9)
u(t) \xleftrightarrow[]{FT}\frac{1}{j\omega}+\pi\delta(\omega) \tag{1-9}
u ( t ) F T
j ω 1 + π δ ( ω ) ( 1 - 9 )
根据FT的线性性质,有:
S
(
ω
)
=
2
j
ω
+
2
π
δ
(
ω
)
−
2
π
δ
(
ω
)
=
2
j
ω
(1-10)
S(\omega)=\frac{2}{j\omega}+2\pi\delta(\omega) -2\pi\delta(\omega)=\frac{2}{j\omega}\tag{1-10}
S ( ω ) = j ω 2 + 2 π δ ( ω ) − 2 π δ ( ω ) = j ω 2 ( 1 - 1 0 )
根据对偶性:
S
(
t
)
=
2
j
t
↔
F
T
2
π
s
g
n
(
−
ω
)
=
−
2
π
s
g
n
(
ω
)
(1-11)
S(t)=\frac{2}{jt}\xleftrightarrow[]{FT}2\pi sgn(-\omega)=-2\pi sgn(\omega) \tag{1-11}
S ( t ) = j t 2 F T
2 π s g n ( − ω ) = − 2 π s g n ( ω ) ( 1 - 1 1 )
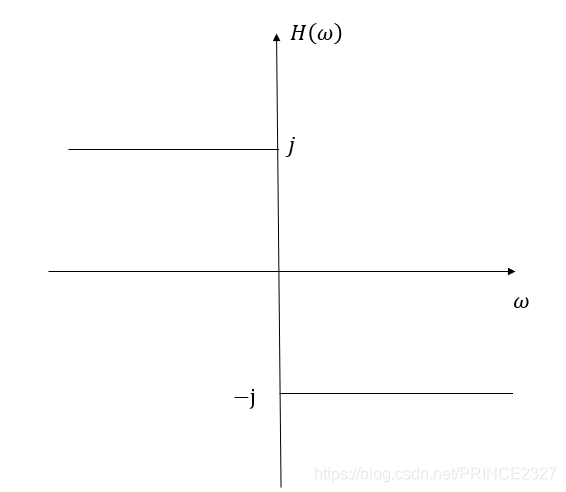
h
(
t
)
=
1
π
t
↔
F
T
−
j
s
g
n
(
w
)
=
H
(
ω
)
(1-12)
h(t)=\frac{1}{\pi t}\xleftrightarrow[]{FT}-jsgn(w)=H(\omega) \tag{1-12}
h ( t ) = π t 1 F T
− j s g n ( w ) = H ( ω ) ( 1 - 1 2 )
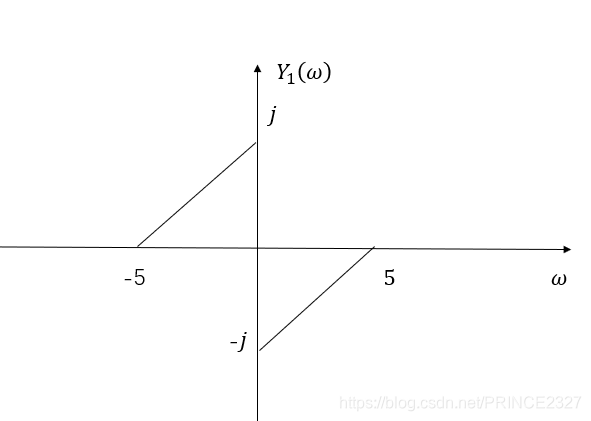
Y
1
(
ω
)
Y_{1}(\omega)
Y 1 ( ω )
Y
2
(
ω
)
Y_{2}(\omega)
Y 2 ( ω )
Y
2
(
ω
)
=
1
2
π
Y
1
(
ω
)
∗
π
j
(
δ
(
ω
−
ω
0
)
−
δ
(
ω
+
ω
0
)
)
(1-13)
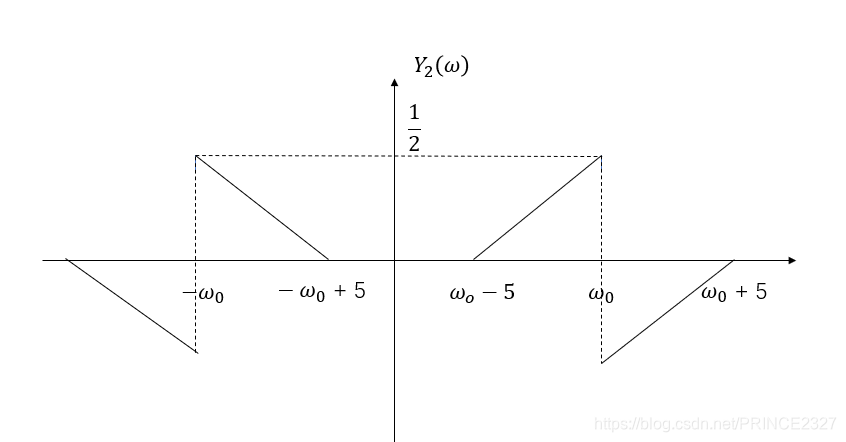
Y_{2}(\omega)=\frac{1}{2\pi} Y_{1}(\omega)*\frac{\pi}{j}(\delta(\omega-\omega_{0})-\delta(\omega+\omega_{0})) \tag{1-13}
Y 2 ( ω ) = 2 π 1 Y 1 ( ω ) ∗ j π ( δ ( ω − ω 0 ) − δ ( ω + ω 0 ) ) ( 1 - 1 3 )
图像如下:
Y
(
ω
)
Y(\omega)
Y ( ω )
Y
(
ω
)
=
Y
2
(
ω
)
+
Y
3
(
ω
)
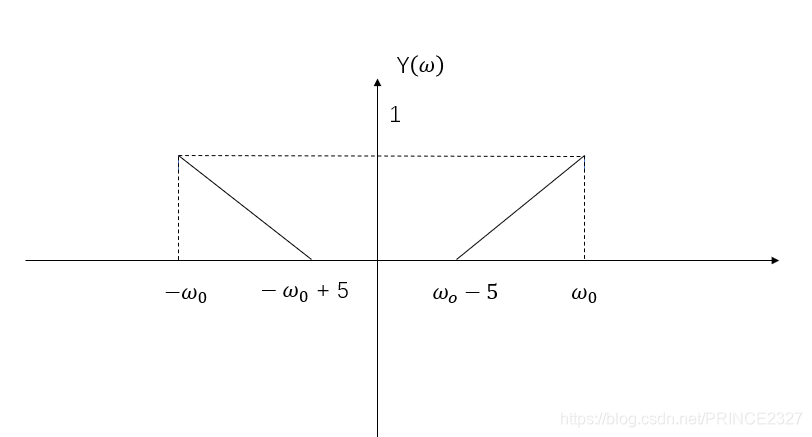
(1-14)
Y(\omega)=Y_{2}(\omega)+Y_{3}(\omega) \tag{1-14}
Y ( ω ) = Y 2 ( ω ) + Y 3 ( ω ) ( 1 - 1 4 )
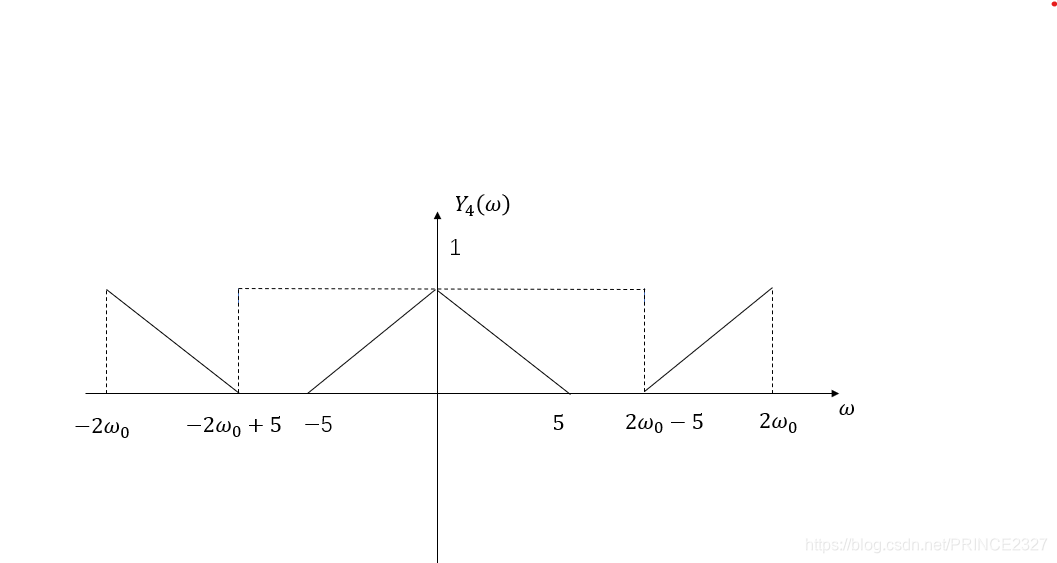
图像如下:对于输入
x
(
t
)
x(t)
x ( t ) 。
b) 先与一个频谱为
H
(
ω
)
=
δ
(
ω
−
ω
0
)
+
δ
(
ω
+
ω
0
)
H(\omega)=\delta(\omega-\omega_{0})+\delta(\omega+\omega_{0})
H ( ω ) = δ ( ω − ω 0 ) + δ ( ω + ω 0 )
Y
4
(
ω
)
Y_{4}(\omega)
Y 4 ( ω )
H
1
(
ω
)
H_{1}(\omega)
H 1 ( ω )
即可恢复出输入信号。
h
1
(
t
)
=
∑
l
=
−
∞
+
∞
δ
(
t
−
l
T
s
)
h_{1}(t)= \sum_{l=-\infty}^{+\infty}\delta(t- lT_{s})
h 1 ( t ) = l = − ∞ ∑ + ∞ δ ( t − l T s )
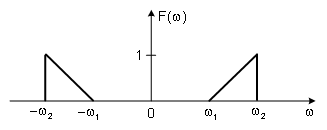
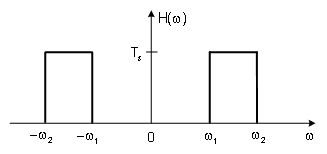
(a)According to the Nyquist sampling theorem, what condition should the sampling angular frequency satisfy?
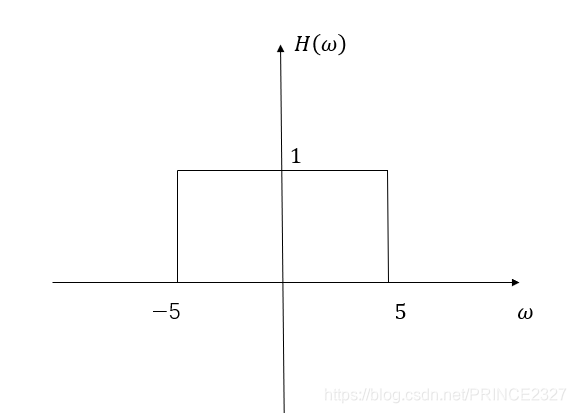
(b)If the filter
H
(
ω
)
H(\omega)
H ( ω )
ω
1
=
ω
2
−
ω
1
\omega_{1}=\omega_{2}-\omega_{1}
ω 1 = ω 2 − ω 1
ω
s
\omega_{s}
ω s
f
(
t
)
f(t)
f ( t )
y
(
t
)
y(t)
y ( t )
ω
s
\omega_{s}
ω s
Solve:
ω
M
=
ω
2
(1-1)
\omega_{M}=\omega_{2}\tag{1-1}
ω M = ω 2 ( 1 - 1 )
ω
s
≥
2
ω
M
=
2
ω
2
(1-2)
\omega_{s} \geq 2\omega_{M}=2\omega_{2} \tag{1-2}
ω s ≥ 2 ω M = 2 ω 2 ( 1 - 2 )
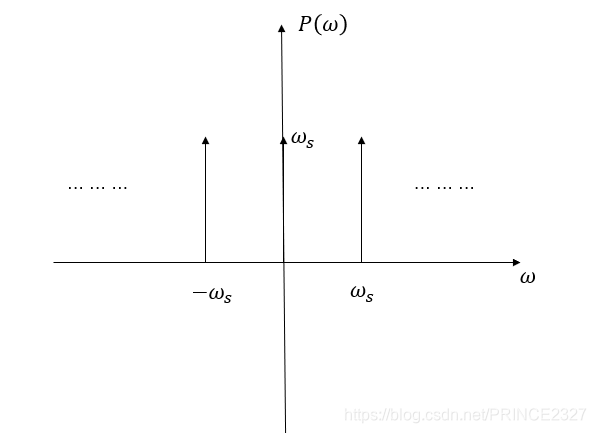
b)
p
(
t
)
p(t)
p ( t )
P
(
ω
)
P(\omega)
P ( ω )
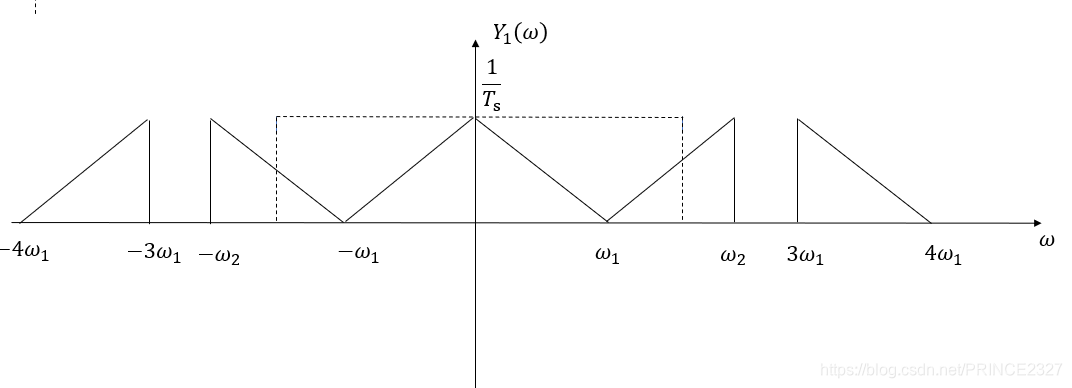
若采样信号不满足奈奎斯特采样定理,即
ω
s
≤
2
ω
2
\omega_{s} \leq 2\omega_{2}
ω s ≤ 2 ω 2
ω
2
=
2
ω
1
\omega_{2}=2\omega_{1}
ω 2 = 2 ω 1
ω
s
=
ω
2
=
2
ω
1
\omega_{s}=\omega_{2}=2\omega_{1}
ω s = ω 2 = 2 ω 1
Y
1
(
ω
)
Y_{1}(\omega)
Y 1 ( ω )
ω
s
=
ω
2
=
2
ω
1
\omega_{s}=\omega_{2}=2\omega_{1}
ω s = ω 2 = 2 ω 1