本来就这题目而言没必要写博客的,不过这个故事挺有意思的,所以还是记录一下。
据说著名犹太历史学家 Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决?Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
其一般形式为:N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。
约瑟夫问题并不难,但求解的方法很多;题目的变化形式也很多。最容易想到的就是模拟杀人过程,代码如下:
int Josephus(int n, int m)
{
//vector<bool>a(n);
bool*a = new bool[n]();
int f = 0, t = 0, s = 0;
do
{
if (t == n)
t = 0;//数组模拟环状,最后一个与第一个相连
if (!a[t])
s++;//第t个位置上有人则报数
if (s == m)//当前报的数是m
{
s = 0;//计数器清零
cout << setw(3)<<t+1 << ' ';//输出被杀人编号(setw需要包含头文件iomanip)
a[t] = 1;//此处人已死,设置为空
f++;//死亡人数+1
if (f % 5 == 0)cout <<endl;
}
++t;//逐个枚举圈中的所有位置
} while (f != n-1);//直到所有人都被杀死为止
for (int i = 0; i < n; i++)
{
if (a[i] == 0)t = i+1;
}
return t;
}
int main()
{
int k = Josephus(41, 3);
cout << "最后剩下:" << k;
}不难发现,这其实是一个O(NM)时间复杂度的暴力解法,对于较大的MN来说效率极低。
想想,我们能否将其转化为递归问题呢?假设约瑟夫函数为f(n,m),即n个人,每数m个人就杀掉一个人,返回值为最后剩下的那个人。问题就在于我们能否通过f(n-1,m)推出f(n,m)呢。
假设f(n-1,m)=k,要推出f(n,m),我们之需要往f(n-1,m)的中再加一个人,那么加在什么位置呢?我们先假设加到n-1个人的后面,很明显我们需要将最后加进去的这个人,调整为第一次杀掉的那个人。那么f(n,m)这个函数第一个杀掉的人就是第m个位置的人,此时这个人在最后的位置,因此我们将其+m之后对n取余,与之对应的f(n-1,m)由k变为了(k+m)%n。
也就是说:
最终剩下一个人时的安全位置肯定为0,反推安全位置在人数为n时的编号
人数为1: 0
人数为2: (0+m) % 2
人数为3: ((0+m) % 2 + m) % 3
人数为4: (((0+m) % 2 + m) % 3 + m) % 4
于是有了如下的递推公式:
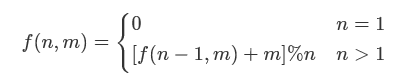
递归写法:
int f(int n, int m) {
if (n == 1)
return 0;
int k = f(n - 1, m);
return (m + k) % n;
}
时间复杂度O(N),空间复杂度O(N)
迭代写法:
int f(int n, int m) {
int k = 0;
for (int i = 2; i != n + 1; ++i)
k = (m + k) % i;
return k;
}
时间复杂度O(N),空间复杂度O(1)
