文章目录

0、前言
1、线性回归的概念

1.1 线性回归的原理
1.2 线性回归的一般形式：
1.3 概率角度的诠释为什么使用均方误差?

2、线性回归损失函数、代价函数与目标函数

2.1 L1正则——Lassio回归
2.2 L2正则——Ridge回归
2.3 Elastic Net回归

3、线性回归的优化方法
3.1 梯度下降法

3.2 最小二乘法矩阵求解
3.3 牛顿法
3.4 拟牛顿法

4、线性回归的评价指标
5、sklearn.linear_model参数详解：

5.1 先尝试调用sklearn的线性回归模型训练数据
5.2 最小二乘法的矩阵求解
参考

0、前言

给定数据集 $\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$ ，其中， $x_i = (x_{i1};x_{i2};x_{i3};...;x_{id}),代表样本；y_i\in R$ 表示目标值。其中 $n$ 表示变量的数量， $d$ 表示每个变量的维度，也就是每个样本的属性。线性模型认为这些特征满足线性关系，通过各个属性的线性组合就可以预测出目标值，而线性模型就是学习每个属性线性组合的方法，形成一个由样本属性到目标值的映射。记为：
$f(x_i)=w_1x_{i1}+w_2x_{i2}+...+w_dx_{id}+b$

向量形式表示为：
$f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b$
其中， $\boldsymbol{w}=(w_1;w_2;...;w_d)$ ， $\boldsymbol{w}与b$ 是需要学习的参数。
线性模型形式简单、易于建模，但却蕴含着机器学习中一些重要的基本思想，许多功能更为强大的非线性模型可以在线性模型的基础上通过引入层级结构或高维映射而得。此外，由于 $\boldsymbol{w}$ 直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性。

本文主要介绍线性回归模型。

1、线性回归的概念

线性回归顾名思义是一个回归模型，模型的额输出是连续值，常常用于股票预测，房价预测等等。

1.1 线性回归的原理

进入一家房产网，可以看到房价、面积、厅室呈现以下数据：

面积( $x_1$ )	厅室数量( $x_2)$	价格 $y$ (万元)
64	3	25
59	3	185
65	3	208
116	4	508
……	……	……

我们可以将价格和面积、厅室数量的关系习得为 $f(x)=\theta_0+\theta_1x_1+\theta_2x_2$ ，使得 $f(x)\approx y$ ，这就是一个直观的线性回归的样式。

1.2 线性回归的一般形式：

根据线性模型有：数据集 $\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$ ； $x_i = (x_{i1};x_{i2};x_{i3};...;x_{id}),代表样本；y_i\in R$ 表示目标值。其中 $n$ 表示变量的数量， $d$ 表示每个变量的维度，也就是每个样本的属性。
可以用以下函数来描述y和x之间的关系：
$\begin{aligned} f(x) &= \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_dx_d \\ &= \sum_{i=0}^{d}\theta_ix_i \\ \end{aligned}$
如何来确定 $\boldsymbol{\theta}$ 的值，使得 $f(x)$ 尽可能接近 $y$ 的值呢？均方误差是回归中常用的性能度量，即：

$J(\theta)=\frac{1}{2}\sum_{j=1}^{n}(h_{\theta}(x^{(i)})-y^{(i)})^2$

我们可以选择 $\theta$ ，试图让均方误差最小化：

$\boldsymbol{\theta}^*=\arg \min_{\theta}J(\boldsymbol{\theta})$

1.3 概率角度的诠释为什么使用均方误差?

下面我们使用极大似然估计，来解释为什么要用均方误差作为性能度量。
极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

我们可以把目标值和变量写成如下等式：

$y^{(i)} = \theta^T x^{(i)}+\epsilon^{(i)}$

$\epsilon$ 表示我们未观测到的变量的影响，即随机噪音。我们假定 $\epsilon$ 是独立同分布，当样本数据集很大时，服从高斯分布。（根据中心极限定理）

$p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}\right)$

因此，

$p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2}\right)$

我们建立极大似然函数，即描述数据遵从当前样本分布的概率分布函数。由于样本的数据集独立同分布，因此可以写成

$L(\theta) = p(\vec y | X;\theta) = \prod^n_{i=1}\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2}\right)$

选择 $\theta$ ，使得似然函数最大化，这就是极大似然估计的思想。

为了方便计算，我们计算时通常对对数似然函数求最大值：
$\begin{aligned} l(\theta) &= log L(\theta) = log \prod^n_{i=1}\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2} {2\sigma^2}\right) \\ & = \sum^n_{i=1}log\frac{1}{\sqrt{2\pi}\sigma}exp\left(-\frac{(y^{(i)}-\theta^T x^{(i)})^2}{2\sigma^2}\right) \\ & = nlog\frac{1}{{\sqrt{2\pi}\sigma}} - \frac{1}{\sigma^2} \cdot \frac{1}{2}\sum^n_{i=1}((y^{(i)}-\theta^T x^{(i)})^2 \end{aligned}$
显然，最大化 $l(\theta)$ 即最小化 $\frac{1}{2}\sum^n_{i=1}((y^{(i)}-\theta^T x^{(i)})^2$ 。

这一结果即均方误差，因此用这个值作为代价函数来优化模型在统计学的角度是合理的。

2、线性回归损失函数、代价函数与目标函数

损失函数(Loss Function)：度量单样本预测的错误程度，损失函数值越小，模型就越好。
代价函数(Cost Function)：度量全部样本集的平均误差。
目标函数(Object Function)：代价函数和正则化函数，最终要优化的函数。

常用的损失函数包括：

0-1损失函数;
平方损失函数;
绝对损失函数;
对数损失函数等。
常用的代价函数包括：
均方误差；
均方根误差；
平均绝对误差等。

既然代价函数已经可以度量样本集的平均误差，为什么还要设定目标函数？

当模型复杂度增加时，有可能对训练集可以拟合的很好，但是测试集的效果不好，出现了过拟合现象，这就出现了所谓的“结构化风险”。结构风险最小化即为了防止过拟合而提出来的策略，定义模型复杂度为 $J(F)$ ，目标函数可表示为：

$\underset{f\in F}{min}\, \frac{1}{n}\sum^{n}_{i=1}L(y_i,f(x_i))+\lambda J(F)$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WqZjcboS-1587453051502)(attachment:image.png)]

例如有以上6个房价和面积关系的数据点，可以看到，当设定 $f(x)=\sum_{j=0}^{5}\theta_jx_j$ 时，可以完美拟合训练集数据，但是，真实情况下房价和面积不可能是这样的关系，出现了过拟合现象。当训练集本身存在噪声时，拟合曲线对未知影响因素的拟合往往不是最好的。
通常，随着模型复杂度的增加，训练误差会减少；但测试误差会先增加后减小。我们的最终目的时试测试误差达到最小，这就是我们为什么需要选取适合的目标函数的原因。
模型复杂度产生的主要原因是 $\theta$ 取值过大，造成斜率过大，曲线就不光滑，为了解决这个问题需要使用正则，一般分为三种：

L1正则
L2正则
Elastic Net 回归

2.1 L1正则——Lassio回归

L1正则指的就是把每个参数的绝对值作为惩罚项加入到目标函数中。
$J(\boldsymbol{\theta})=\frac{1}{2}\sum\limits_{i=1}^nL(y_i,f(x_i))+\lambda\sum_{j=1}^d|\theta_j|$

2.2 L2正则——Ridge回归

L2正则指的是把每个参数的平方作为惩罚项加入到目标函数中。
$J(\boldsymbol{\theta})=\frac{1}{2}\sum\limits_{i=1}^nL(y_i,f(x_i))+\lambda\sum_{j=1}^d(\theta_j)^2$

2.3 Elastic Net回归

Elastic Net回归指的是将L1正则和L2正咋按一定比例混合起来。
$J(\boldsymbol{\theta})=\frac{1}{2}\sum\limits_{i=1}^nL(y_i,f(x_i))+\lambda(\rho\sum_{j=1}^d|\theta_j|+(1-\rho)\sum_{j=1}^d(\theta_j)^2)$
L1正则会趋向于产生少量的特征，其他的特征都是0，而L2正则会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下，选择Lasso比较合适，因为它能自动选择特征。而如果所有特征中，大部分特征都能起作用，而且起的作用很平均，那么使用Ridge也许更合适。

3、线性回归的优化方法

3.1 梯度下降法

设定初始参数 $\theta$ ,不断迭代，使得 $J(\theta)$ 最小化：

$\theta_j:=\theta_j-\alpha\frac{\partial{J(\theta)}}{\partial\theta}$

其中导数为：
$\begin{aligned} \frac{\partial{J(\theta)}}{\partial\theta} &= \frac{\partial}{\partial\theta_j}\frac{1}{2}\sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})^2 \\ &= 2*\frac{1}{2}\sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})*\frac{\partial}{\partial\theta_j}(f_\theta(x)^{(i)}-y^{(i)}) \\ &= \sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})*\frac{\partial}{\partial\theta_j}(\sum_{j=0}^{d}\theta_jx_j^{(i)}-y^{(i)}))\\ &= \sum_{i=1}^{n}(f_\theta(x)^{(i)}-y^{(i)})x_j^{(i)} \\ \end{aligned}$
即：

$\theta_j = \theta_j + \alpha\sum_{i=1}^{n}(y^{(i)}-f_\theta(x)^{(i)})x_j^{(i)}$

注：下标j表示第 $j$ 个参数，上标 $i$ 表示第 $i$ 个数据点。

将所有的参数以向量形式表示，可得：

$\theta = \theta + \alpha\sum_{i=1}^{n}(y^{(i)}-f_\theta(x)^{(i)})x^{(i)}$

由于这个方法中，参数在每一个数据点上同时进行了移动，因此称为批梯度下降法，对应的，我们可以每一次让参数只针对一个数据点进行移动，即：

$\theta = \theta + \alpha(y^{(i)}-f_\theta(x)^{(i)})x^{(i)}$

这个算法成为随机梯度下降法，随机梯度下降法的好处是，当数据点很多时，运行效率更高；缺点是，因为每次只针对一个样本更新参数，未必找到最快路径达到最优值，甚至有时候会出现参数在最小值附近徘徊而不是立即收敛。但当数据量很大的时候，随机梯度下降法经常优于批梯度下降法。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mMIrixGD-1587453051504)(attachment:image.png)]

当 $J$ 为凸函数时，梯度下降法相当于让参数 $\theta$ 不断向J的最小值位置移动

梯度下降法的缺陷：如果函数为非凸函数，有可能找到的并非全局最优值，而是局部最优值。
批量梯度下降法（BGD）、随机梯度下降法（SGD）和小批量梯度下降法（MBGD）对比：

1.批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。
优点：
1. 一次迭代是对所有样本进行计算，此时利用矩阵进行操作，可实现并行。
2. 由全数据集确定的方向能更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，一定能找到全局最优。
缺点：
1. 当样本数目较大时，每迭代一次就要对所有样本进行计算，训练过程慢。
2.随机梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。
优点：
1. 一次迭代只对一个样本进行计算，然后更新参数，训练速度大大加快。
缺点：
1. 准确率下降，即使是凸函数也不一定能收敛到全局最优。
2. 单个样本不能代表训练集的总体趋势，每次只计算一个样本，不易于并行计算。
3.小批量梯度下降，是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代使用batch_size 个样本来对参数进行更新。
优点：
1. 通过矩阵运算，每一个batch更新网络参数速度比单个样本慢不了多少。
2. 每次使用一个batch，可以大大减少收敛所需要的迭代次数，更接近梯度下降的效果。
3. 可以实现并行计算
缺点：
1. 每一个batch的大小选择可能会造成一些问题。

3.2 最小二乘法矩阵求解

令

$X = \left[ \begin{array} {cccc} (x^{(1)})^T\\ (x^{(2)})^T\\ \ldots \\ (x^{(n)})^T \end{array} \right]$

其中，

$x^{(i)} = \left[ \begin{array} {cccc} x_1^{(i)}\\ x_2^{(i)}\\ \ldots \\ x_d^{(i)} \end{array} \right]$

由于

$Y = \left[ \begin{array} {cccc} y^{(1)}\\ y^{(2)}\\ \ldots \\ y^{(n)} \end{array} \right]$

$h_\theta(x)$ 可以写作

$h_\theta(x)=X\theta$

对于向量来说，有

$z^Tz = \sum_i z_i^2$

因此可以把损失函数写作

$J(\theta)=\frac{1}{2}(X\theta-Y)^T(X\theta-Y)$

为最小化 $J(\theta)$ ,对 $\theta$ 求导可得：
$\begin{aligned} \frac{\partial{J(\theta)}}{\partial\theta} &= \frac{\partial}{\partial\theta} \frac{1}{2}(X\theta-Y)^T(X\theta-Y) \\ &= \frac{1}{2}\frac{\partial}{\partial\theta} (\theta^TX^TX\theta - Y^TX\theta-\theta^T X^TY - Y^TY) \\ \end{aligned}$
中间两项互为转置，由于求得的值是个标量，矩阵与转置相同，因此可以写成
$\begin{aligned} \frac{\partial{J(\theta)}}{\partial\theta} &= \frac{1}{2}\frac{\partial}{\partial\theta} (\theta^TX^TX\theta - 2\theta^T X^TY - Y^TY) \\ \end{aligned}$

令偏导数等于零，由于最后一项和 $\theta$ 无关，偏导数为0。
因此，

$\frac{\partial{J(\theta)}}{\partial\theta} = \frac{1}{2}\frac{\partial}{\partial\theta} \theta^TX^TX\theta - \frac{\partial}{\partial\theta} \theta^T X^TY$

利用矩阵求导性质:
$\frac{\partial \vec x^T\alpha}{\partial \vec x} =\alpha$
和

$\frac{\partial A^TB}{\partial \vec x} = \frac{\partial A^T}{\partial \vec x}B + \frac{\partial B^T}{\partial \vec x}A$

$\begin{aligned} \frac{\partial}{\partial\theta} \theta^TX^TX\theta &= \frac{\partial}{\partial\theta}{(X\theta)^TX\theta}\\ &= \frac{\partial (X\theta)^T}{\partial\theta}X\theta + \frac{\partial (X\theta)^T}{\partial\theta}X\theta \\ &= 2X^TX\theta \end{aligned}$

$\frac{\partial{J(\theta)}}{\partial\theta} = X^TX\theta - X^TY$

令导数等于零，

$X^TX\theta = X^TY$

$\theta = (X^TX)^{(-1)}X^TY$

若 $(X^TX)$ 可逆，则上式正确。
若 $(X^TX)$ 不可逆，可以增加 $\lambda$ 扰动， $X^TX+\lambda I$ 正定：

$\theta = (X^TX+\lambda I)^{(-1)}X^TY$

3.3 牛顿法

在这里插入图片描述
通过图例可知(参考吴恩达CS229),

$f(\theta)' = \frac{f(\theta)}{\Delta},\Delta = \theta_0 - \theta_1$

$可求得，\theta_1 = \theta_0 - \frac {f(\theta_0)}{f(\theta_0)'}$

重复迭代，可以让逼近取到 $f(\theta)$ 的最小值

当我们对损失函数 $l(\theta)$ 进行优化的时候，实际上是想要取到 $l'(\theta)$ 的最小值，因此迭代公式为：

$\theta :=\theta-\frac{l'(\theta)}{l''(\theta)}$

$当\theta是向量值的时候，\theta :=\theta - H^{-1}\Delta_{\theta}l(\theta)$

其中， $\Delta_{\theta}l(\theta)$ 是 $l(\theta)$ 对 $\theta_i$ 的偏导数， $H$ 是 $J(\theta)$ 的海森矩阵，

$H_{ij} = \frac{\partial ^2l(\theta)}{\partial\theta_i\partial\theta_j}$

问题：请用泰勒展开法推导牛顿法公式。

Answer：将 $f(x)$ 用泰勒公式展开到第二阶，

$f(x) = f(x_0) + f'(x_0)(x - x_0)+\frac{1}{2}f''(x_0)(x - x_0)^2$

对上式求导，并令导数等于0，求得x值

$f'(x) = f'(x_0) + f''(x_0)x -f''(x_0)x_0 = 0$

可以求得，

$x = x_0 - \frac{f'(x_0)}{f''(x_0)}$

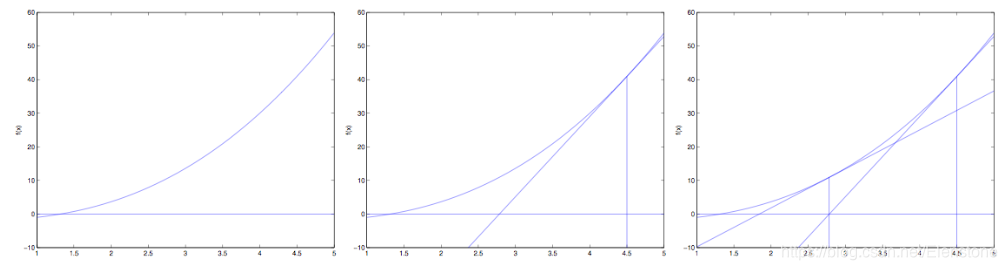
牛顿法的收敛速度非常快，但海森矩阵的计算较为复杂，尤其当参数的维度很多时，会耗费大量计算成本。我们可以用其他矩阵替代海森矩阵，用拟牛顿法进行估计，

3.4 拟牛顿法

拟牛顿法的思路是用一个矩阵替代计算复杂的海森矩阵H，因此要找到符合H性质的矩阵。

要求得海森矩阵符合的条件，同样对泰勒公式求导 $f'(x) = f'(x_0) + f''(x_0)x -f''(x_0)x_0$

令 $x = x_1$ ，即迭代后的值，代入可得：

$f'(x_1) = f'(x_0) + f''(x_0)x_1 - f''(x_0)x_0$

更一般的，

$f'(x_{k+1}) = f'(x_k) + f''(x_k)x_{k+1} - f''(x_k)x_k$

$f'(x_{k+1}) - f'(x_k) = f''(x_k)(x_{k+1}- x_k)= H(x_{k+1}- x_k)$

$x_k$ 为第k个迭代值

即找到矩阵G，使得它符合上式。
常用的拟牛顿法的算法包括DFP，BFGS等，作为选学内容，有兴趣者可自行查询材料学习。

4、线性回归的评价指标

均方误差(MSE): $\frac{1}{m}\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2$

均方根误差(RMSE)： $\sqrt{MSE} = \sqrt{\frac{1}{m}\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2}$

平均绝对误差(MAE)： $\frac{1}{m}\sum^{m}_{i=1} | (y^{(i)} - \hat y^{(i)} |$

但以上评价指标都无法消除量纲不一致而导致的误差值差别大的问题，最常用的指标是 $R^2$ ,可以避免量纲不一致问题

$R^2: = 1-\frac{\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2}{\sum^{m}_{i=1}(\bar y - \hat y^{(i)})^2} =1-\frac{\frac{1}{m}\sum^{m}_{i=1}(y^{(i)} - \hat y^{(i)})^2}{\frac{1}{m}\sum^{m}_{i=1}(\bar y - \hat y^{(i)})^2} = 1-\frac{MSE}{VAR}$

我们可以把 $R^2$ 理解为，回归模型可以成功解释的数据方差部分在数据固有方差中所占的比例， $R^2$ 越接近1，表示可解释力度越大，模型拟合的效果越好。

5、sklearn.linear_model参数详解：

fit_intercept : 默认为True,是否计算该模型的截距。如果使用中心化的数据，可以考虑设置为False,不考虑截距。注意这里是考虑，一般还是要考虑截距
normalize: 默认为false. 当fit_intercept设置为false的时候，这个参数会被自动忽略。如果为True,回归器会标准化输入参数：减去平均值，并且除以相应的二范数。当然啦，在这里还是建议将标准化的工作放在训练模型之前。通过设置sklearn.preprocessing.StandardScaler来实现，而在此处设置为false
copy_X : 默认为True, 否则X会被改写
n_jobs: int 默认为1. 当-1时默认使用全部CPUs ??(这个参数有待尝试)

可用属性：

coef_:训练后的输入端模型系数，如果label有两个，即y值有两列。那么是一个2D的array
intercept_: 截距

可用的methods:

fit(X,y,sample_weight=None):
X: array, 稀疏矩阵 [n_samples,n_features]
y: array [n_samples, n_targets]
sample_weight: 权重 array [n_samples]
在版本0.17后添加了sample_weight
get_params(deep=True)：返回对regressor 的设置值
predict(X): 预测基于 R^2值
score：评估

参考https://blog.csdn.net/weixin_39175124/article/details/79465558

生成数据

#生成数据
import numpy as np
#生成随机数
np.random.seed(1234)
x = np.random.rand(500,3)
#构建映射关系，模拟真实的数据待预测值,映射关系为y = 4.2 + 5.7*x1 + 10.8*x2，可自行设置值进行尝试
y = x.dot(np.array([4.2,5.7,10.8]))

5.1 先尝试调用sklearn的线性回归模型训练数据

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline

# 调用模型
lr = LinearRegression(fit_intercept=True)
# 训练模型
lr.fit(x,y)
print("估计的参数值为：%s" %(lr.coef_))
# 计算R平方
print('R2:%s' %(lr.score(x,y)))
# 任意设定变量，预测目标值
x_test = np.array([2,4,5]).reshape(1,-1)
y_hat = lr.predict(x_test)
print("预测值为: %s" %(y_hat))

估计的参数值为：[ 4.2  5.7 10.8]
R2:1.0
预测值为: [85.2]

5.2 最小二乘法的矩阵求解

class LR_LS():
    def __init__(self):
        self.w = None      
    def fit(self, X, y):
        # 最小二乘法矩阵求解
        #============================= show me your code =======================
        self.w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
        #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        #============================= show me your code =======================
        y_pred = X.dot(self.w)
        #============================= show me your code =======================
        return y_pred

if __name__ == "__main__":
    lr_ls = LR_LS()
    lr_ls.fit(x,y)
    print("估计的参数值：%s" %(lr_ls.w))
    x_test = np.array([2,4,5]).reshape(1,-1)
    print("预测值为: %s" %(lr_ls.predict(x_test)))

估计的参数值：[ 4.2  5.7 10.8]
预测值为: [85.2]

3、梯度下降法

class LR_GD():
    def __init__(self):
        self.w = None     
    def fit(self,X,y,alpha=0.02,loss = 1e-10): # 设定步长为0.002,判断是否收敛的条件为1e-10
        y = y.reshape(-1,1) #重塑y值的维度以便矩阵运算
        [m,d] = np.shape(X) #自变量的维度
        self.w = np.zeros((d)) #将参数的初始值定为0
        tol = 1e5
        #============================= show me your code =======================
        while tol > loss:
            h_f = X.dot(self.w).reshape(-1,1) 
            theta = self.w + alpha*np.mean(X*(y - h_f),axis=0) #计算迭代的参数值
            tol = np.sum(np.abs(theta - self.w))
            self.w = theta
        #============================= show me your code =======================
    def predict(self, X):
        # 用已经拟合的参数值预测新自变量
        y_pred = X.dot(self.w)
        return y_pred  

if __name__ == "__main__":
    lr_gd = LR_GD()
    lr_gd.fit(x,y)
    print("估计的参数值为：%s" %(lr_gd.w))
    x_test = np.array([2,4,5]).reshape(1,-1)
    print("预测值为：%s" %(lr_gd.predict(x_test)))

估计的参数值为：[ 4.20000001  5.70000003 10.79999997]
预测值为：[85.19999995]

参考

吴恩达 CS229课程

周志华《机器学习》

李航《统计学习方法》

https://hangzhou.anjuke.com/

https://www.jianshu.com/p/e0eb4f4ccf3e

https://blog.csdn.net/qq_28448117/article/details/79199835

https://blog.csdn.net/weixin_39175124/article/details/79465558

Elenstone

原创文章 58 获赞 7 访问量 6198

关注私信

机器学习最易懂之线性回归模型的基本原理和python实现