目录
1、计算几何是什么?
计算几何研究的对象是几何图形。对于图像的研究一般都是先建立坐标系,把图形转换成函数,然后用插值和逼近的数学方法,特别是用样条函数作为工具来分析图形。
然而这些方法过多地依赖于坐标系的选取,缺乏几何不变性,特别是用来解决某些大挠度曲线及曲线的奇异点等问题时,有一定的局限性。
2、计算几何理论中过两点的一条直线的表达式是如何描述的?
在任意维度中,由两点P0、P1定义的直线参数方程式,当参数s为实数且u=P1-P0为直线的方向向量时可以表示为P(s) = P0 + s (P1-P0) = P0 + su

当P(s)是有限线段P0P1上的一个点且0<s<1时,用表达式P(0)=P0, P(1)=P1,s = d(P0,P(s)) / d(P0,P1). 更进一步, 如果s<0,P(s)在线段P0之外,如果if s>1,P(s) 在线段P1的外侧。
3、凸集是什么? 直线是凸集吗?是仿射集吗?
凸集
在凸几何中,凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说,在欧氏空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内。
令S是实数上的向量空间,或者更一般地,是在某个有序域上,这包括欧几里德空间。如果对于C中的所有x和y,并且在区间(0,1)中的所有t,点(1-t)x+ty也属于C,则S中的集合C被称为凸。换句话说,连接x和y的线段上的每个点都在C中。这意味着实际或复杂拓扑向量空间中的凸集是路径连接的。此外,如果除了端点之外的连接x和y的线段上的每个点都在C的内部,则C是严格凸起的。
比如说,立方体是凸集,但是任何中空的或具有凹痕的例如月牙形都不是凸集。
仿射
仿射定义:对于集合Cϵ{R^n},如果通过集合C中任意两个不同点之间的直线仍在集合C中,则称集合C为仿射(affine)。
也就是说,C包括了在C中任意两点的线性组合直线是仿射集而所有的仿射集都是凸集。根据定义,仿射集是组合的直线在仿射集内,那么直线肯定在集合内,所以是凸集。
4、三维空间中的一个平面,如何表达?
平面方程:Ax+By+Cz+D=0 (参数,A,B,C,D是描述平面空间特征的常数)
平面方程可用于判定空间中一点与对象的多边形面片的相对位置关系,对任意点(x,y,z)。如果不在参数为A,B,C,D的平面上,则Ax+By+Cz+D不等于0;如果 Ax+By+Cz+D<0,则(x,y,z)在平面;Ax+By+Cz+D>0,则(x,y,z)在平面前方
对于平面方程 Ax+By+Cz+D=0,法向量表示此平面的空间方向,法向量与平面垂直
且以(A,B,C)为其坐标分量,法向量从平面内部指向外部
5、更高维度的“超平面”,如何表达?
超平面H是从n维空间到n-1维空间的一个映射子空间,它有一个n维向量和一个实数定义。因为是子空间,所以超平面一定过原点。
通常,R2(二维空间)中的点集 i = (x,y)满足等式 (点集 i 实际为一条直线):ax + 1/by + c = 0 (1)
其中,a,b,c为标量;a,1/b至少有一个不为0。我们假设 b 不为0。那么 y = -abx - cb
使用换元法,令 t = x,(显然,t 为标量) 则点集 i (x,y) 可以表示成 i (x,y) = ( t, -abt - cb) = t (1, -ab) + (0, -cb)这条直线实际上就是过 (0, -cb) 点,方向为 (1, -ab) 的直线 L。
令向量 n = (a,1/b),则 (1)可以表示成n* i + c = 0 (2)
假设在直线 L 上取一点 p0(x0,y0),显然,n* p0 + c = 0,那么 c = -n* p0。
将 (2)改写,可得 n* i-n* p0 = 0 ,即可 n* (i - p0 ) = 0。
因为 n 和(i - p0 ) 均是向量,(i - p0 ) 在直线 L 上, 所以,n 垂直直线L ,即n为直线L 的法向量。我们可以得到那些与p的差向量与 n 向量正交的点,就是点集 i (x,y).
给定向量空间 Rn 中的一个点 P 和一个非零向量n ,满足 n * (i - p)= 0则称点集 i 为通过点p 的超平面,向量 n为通过超平面的法向量。按照这个定义,虽然当维度大于3才可以成为“超”平面,但是你仍然可以认为,一条直线是 R2 空间内的超平面,一个平面是 R3 空间内的超平面 。Rn 空间的超平面是Rn 空间内的一个 n - 1 维的仿射子空间。
6、凸函数定义?如何判别一个函数是凸函数?
凸函数:
对于一元函数 f(x) ,如果对于任意 t ϵ[0,1 ]均满足:f(tx1+(1−t)x2)≤tf(x1)+(1−t)f(x2),则称f(x)为凸函数(convex function)。
如果对于任意 t ϵ(0,1)均满足:f(tx1+(1−t)x2)<tf(x1)+(1−t)f(x2),则称f(x)为严格凸函数(convex function)。
从几何上直观地理解凸函数的特点,凸函数的割线在函数曲线的上方,如图所示:

由上面的公式,可以推广到多元函数。在数据科学的模型求解中,如果优化的目标函数是凸函数,则局部极小值就是全局最小值。这也意味着我们求得的模型是全局最优的,不会陷入到局部最优值。例如支持向量机的目标函数||w||2/2就是一个凸函数。
判别函数是否为凸函数
对于一元函数f(x),我们可以通过其二阶导数f′′(x) 的符号来判断。如果函数的二阶导数总是非负,即f′′(x)≥0 ,则f(x)是凸函数。
对于多元函数f(X),我们可以通过其Hessian矩阵(Hessian矩阵是由多元函数的二阶导数组成的方阵)的正定性来判断。如果Hessian矩阵是半正定矩阵,则是f(X)凸函数。
7、什么是凸规划?如何判别一个规划问题是凸规划问题。举例说明?
凸规划
最优化问题的目标函数为凸函数,不等式约束函数也为凸函数,等式约束函数是仿射的,则称该最优化问题为凸规划。凸规划的可行域为凸集。
若最优化问题的目标函数为凸函数,不等式约束函数也为凸函数,等式约束函数是仿射的,则称该最优化问题为凸规划。凸规划的可行域为凸集,因而凸规划的局部最优解就是它的全局最优解。当凸规划的目标函数为严格凸函数时,若存在最优解,则这个最优解一定是唯一的最优解。
举例
例子1:如下非线性规划是否为凸规划


例子2:验证下列(MP)是凸规划
解:
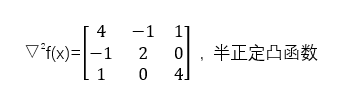

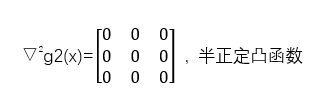

由上述四个式子可证为凸规划。
