路径规划：D*Lite寻路算法详解

D*Lite详解目录

一、简介

1. 关于算法
2. 关于本文

二、算法相关概念解释

1. 基本概念
2. 变量
3. 更多术语

三、主要公式、过程&说明

1. G值和Rhs值
2. Key值和Queue（优先队列）
3. Dequeue（寻路函数主要过程）

四、整体框架

五、伪代码&解析

六、例子

七、主要源码

八、Unity完整演示项目

1. 纯演示预览
2. 完整项目

一、简介

1.关于算法

       D*Lite算法是Sven Koenig 和Maxim Likhachev 在2002年基于LPA*算法基础上提出的动态路径规划算法。它的优点是可以利用首次计算路径的信息动态规划路径。因此它可以应用于机器人在未知环境中的动态寻路。

D*Lite要解决的问题：

• 当再次寻路时，如果直接完全重新计算，那么固然会有很多重复运算，我们希望把上次寻路的数据利用起来。

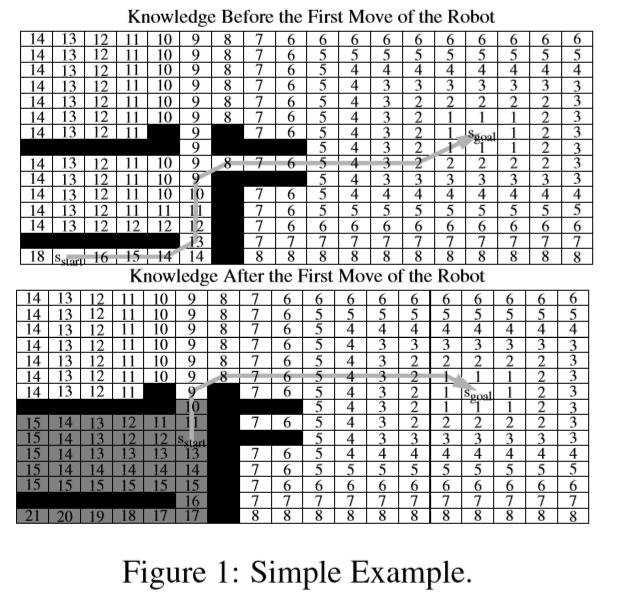
• 所以我们只需要处理终点到起点启发值改变的部分（下图中灰色部分）。然而这还不够好，因为事实上影响我们寻路的只有其中的很少一部分（Start→11→10三个点）。

       所以D*Lite算法就是为了识别并处理这些真正影响到最终路径的点，而尽量忽略无关点的运算，从而提升再次寻路时的运算效率。

D*Lite存在的不足：
       只有当地图发生局部变化时才有优势，如果地图整体上变动过大，修正路径的用时甚至比直接重新计算要长。 所以当地图过小或处于其它容易发生地图全局变动的情况下不建议使用。

2.关于本文

       论文中该算法有2个版本，本文介绍的是第2版。
       D*Lite算法其实是不错的动态寻路算法，但是国内并没有很多详细介绍的文章……因此我打算把我看到的和理解到的都在本文总结起来。如果部分理解有误，请谅解。
       本文不涉及任何人工智能的知识，只是单纯讨论算法。而且（因为我是搞游戏的），所以最后的代码及演示会涉及到Unity。
       本文会在各个环节逐步渗透算法的原理，也许在开始时会很难理解，但会在后面进行整个算法的总结。
       文章中用到的例子是MIT公开课的例子，如果有时间可以去康康整节课程，讲的很不错（链接见下）
       当然想要完全弄透这个算法估计一篇文章还不够，还需要参考更多的资料，在这里列出一些比较好的资源：
LPA* 路径搜索算法介绍_肚皮朝上的刺猬的博客
D* Lite路径规划算法_云水禅心的博客
YouTube上的MIT公开课 Advanced 1. Incremental Path Planning
D*Lite论文原文

二、算法相关概念解释

1.基本概念

       算法把地图分为若干个块（结点），每个块有自己的变量记录状态和数值。全局有一个队列来决定对哪个结点进行检测并更改。经过一系列检测后会根据每个块的数值，（使用贪婪算法）决定选择哪条路。

• 障碍物： 本文的障碍物都是指中途改变的障碍物。因为动态路径算法我们更关注中途障碍如何应对，所以我们只讨论中途障碍物，该算法自然也能应对初始障碍物的，不过在此不做详细分析。

• s： s表示上述的一个地图块（结点）

• predecessor： 前继点。可以到达该结点的所有其它结点，都称为该结点的前继点。
  下图中，蓝点可以到达红点，所以蓝点是红点的predecessor（前继点）
  

• successor： 后继点。可以从该结点行进到的所有其它结点，都称为该结点的后继点。
  下图中，红点可以到达蓝点，所以蓝点是红点的successor（后继点）
  

• PriorityQueue(又叫U)： 待检测队列，里面按Key（下面提及的）大小存放待检测更新的结点。

• Key： 键值，用于上面说的queue（队列），当结点可能需要被检测时，需要加入queue，此时需要先为其按情况生成Key；对同一结点，不同情况会产生不同的Key，Key将成为寻路时结点检测先后顺序的依据。（具体计算方式后面介绍）

• Dequeue： 取出队列中的一个元素并进行检测，并按一定条件改变它的值。在此算法中将永远先取出Key值最小的元素。（后面继续解释）
  值得注意的一点是：
  99%的结点数值更新都只发生在此过程，这是算法的主要过程，其它过程一般不改变结点的相关变量值。（剩下1%是中途障碍物直接影响）

2.变量

• EdgeCost值： 该值表示两个相邻结点之间移动需要多少花费。（常用距离来估计）
  比如相邻节点A,B EdgeCost为10，意味着在A移动到B（或相反）耗费为10。

• G值： 该值表示该结点到终点的花费值，值是由下面说的Rhs给予的。
         在此算法中，G值可以意味着该结点到终点的最少耗费，但这不意味着G值在多次运算中具有实时性，当障碍物改变时，它会过时（不会及时变更，即可能不完全准确），然后不准确结点的G值在再次寻路被需要时重新计算。
         一旦某结点的G值改变，它的影响会立刻作用到相邻（这点具体后面讲），正因如此，如果我们不改变不必要的G值，那么就可以减少相邻节点的无效计算。（这一个是逐个传递的，一个G值改变会影响相邻结点G值改变，由此观之不计算不必要的G值能有很大性能提升）

• Rhs值(Right Hand Side)： 描述当前结点到终点的花费值。（没错，与G值一样，事实上G值是由Rhs值给予的，即G=Rhs），Rhs值由终点起到该结点的EdgeCost依次累加起来。（是这么定义的，但是计算时我们不直接这么做，因为会造成很多重复运算）

G值和Rhs值的联系：

1. G值在特定条件时由Rhs值赋值，即一次运算中永远先更新Rhs，后更新G
2. 并非所有更新过的Rhs值都会赋值给对应结点的G（只有需要用到时才会赋值）
3. 当发生G=Rhs赋值时，意味着G值改变，该结点的影响会立刻传递到它的predecessor（如前述）
4. 单单Rhs值发生改变并不会把影响传递到临近predecessor
5. 每次障碍改变时先更新Rhs值，可以粗略理解为Rhs为更新过的G

• H值(heuristic)： 启发值，表示该点到起点的花费，可用坐标差或其它形式估算。
• Km值(KeyModifier)： 键值修饰器，用于修饰Key，改变Key的值，它可以让Key与Key之间的数值比较对于实际而言更有意义（Key是结点在Queue中排列的依据，也就是说这个Km是改变Queue中结点的顺序，让其排序更加合理）

3.更多术语

• UpdateVertex()： 更新结点的函数，事实上是更新结点在Queue中的状态。它决定了该结点是否应该加入队列/在队列中更新Key值/移出队列。（具体判断规则在状态介绍完毕后会补充）
  当结点在以下情况时会触发该函数：
  • 当结点被Dequeue过程处理完时，需要判断它是否需要再次加入队列
  • 当结点G值改变时，影响传递到所有predecessor，将对所有predecessor进行UpdateVertex
  • 当结点受障碍物直接影响时，对其自身与所有predecessor进行UpdateVertex
• 传递： 之前提到多次，其实就是进行结点更新，即调用UpdateVertex，这里再说一次只是为了强调

三个状态：

       在Queue（优先队列）中的结点我们会按照Key的顺序依次对它们进行检测（Dequeue）。检测到的状态分为如下三种，每种状态在Dequeue时会有不同的效果：

• Locally Consistent： 局部一致。当一个结点G=Rhs时为此状态。此状态表示结点处于预估与实际基本没有差错的稳定状态。如无外界障碍物改变，将一直保持此状态。被Dequeue后就不会被再次纳入Queue（检测队列）。

• Locally Overconsistent： 局部过一致。当一个结点G>Rhs时为此状态。Rhs更新后比G小，这意味着该结点如今的连通状态比之前要好。（可能障碍物被移除了）当Dequeue时检测到某结点为该状态时，会发生三件事：

  • 令G=Rhs（因为它更好了，我们有理由把耗费降低到新的预估值）
  • 将影响传递到所有predecessor（因为G值改变了）
           在D*Lite的第二个版本中，这一步还会立刻尝试检测这个更新后的结点是否为它predecessor的更好successor，如果是，则把Rhs（终点花费估计）值设置为经由该点的值，否则将保留predecessor原来的Rhs
  • 如无外界障碍物改变，将一直保持在consistent状态

• Locally Underconsistent： 局部欠一致。当一个结点G<Rhs时为此状态。Rhs更新后比G大，这种情况只会出现在障碍物中途出现时，这意味着该结点已受到附近新障碍物的直接/间接影响，很可能已经不是一条最好的路径了（甚至走不通）。当Dequeue时检测到某结点为该状态时，会发生三件事：

  • 令G=∞（因为它被暂时判定为“不连通”，花费为无限）
  • 将影响传递到所有predecessor（因为G值改变了）
           在D*Lite的第二个版本中，这一步还会立刻尝试对这些受影响的predecessor立刻找一个更好的successor。体现为把自身Rhs（终点花费估计值）设置为它所有successor中最低的
  • 将它再次加入Queue以作进一步判断

       另外：当执行UpdateVertex（更新结点）函数时，非稳定状态（即除Consistent状态）的结点会被立即加入PriorityQueue

三、主要公式、过程&说明

定义EdgeCost：

$c(s,s')$

计算G（理论上）：

$g(s)=\left\{ \begin{aligned} &0&&, if(s==s_{goal}) &\\ &min_{s'\in succ(s)}(g(s')+c(s,s')&&,otherwise& \end{aligned} \right.$

实际上我们使用G=Rhs对G赋值，所以接下来大概也能猜到Rhs的公式是啥了……

计算Rhs：

$rhs(s)=\left\{ \begin{aligned} &0&&, if(s==s_{goal}) &\\ &min_{s'\in succ(s)}(g(s')+c(s,s')&&,otherwise& \end{aligned} \right.$

关于如何获取正确的G值与Rhs值：

       注意到这里的rhs是根据successor的G值求的，意味着我们如果要得到正确的rhs(s)，就必须先得到正确的g(s’)。那么我们怎么做到这一点呢？

1.当第一次计算时：

       我们可以从公式观察到，Sgoal的Rhs==0是已知的，事实上我们会把所有除Sgoal以外的Rhs值，包括Sgoal的所有G值初始化为∞
       此时Sgoal处于Overconsistent，此时我们会对Sgoal进行Dequeue，进而对终点进行赋值G=Rhs，此时由于Sgoal的G值改变会影响周围predecessor
       然后我们会为所有predecessor计算Rhs，然后predecessor会处于Overconsistent状态，加入Queue，继续Dequeue就可以得到这个predecessor的准确G值，然后继续向predecessor的predecessor传递这些影响……
        如此递推下去，第一次计算就可以获得任意结点的准确G值与Rhs值

2.当障碍物改变时：

        正如前所述，我们的G值不会立刻改变，而且它会过时（可能不再完全准确），我们此时分两种情况，但仍然先按照旧的G值判断。

2.1.当障碍物消失时：

       我们结合一个例子分析受EdgeCost减少影响的局部范围内的结点。
       如果EdgeCost减少发生在图中红点与右方白点之间（下两图中右边6→1的地方）。那么对于 G<G(红点) 的结点，（即图中右边的两点），它们更靠近Sgoal，所以它们的G值不可能依赖于红点（虽然例子中的箭头是单向通道，固然不依赖，但我在此强调的是，假设它是双向通道，它们的G值也不依赖于红点！！！），而是某些更靠近终点的点（不在图中展示），因此障碍物消失的影响与右边的点无关，它们的G值仍然是正确的。 这其实是动态规划的一种体现。
       而相对的，对于左边三个白点，它们的G值在第一次计算时是由红点传递过去的，根据公式，它们的G值应该是G = G(红点)+Cost(红点,自己)。显然这个值是>G(红点)的。也就是说：对于G>G(红点)的点，它们之中可能有一部分依赖于红点（在这例子中左边的白点都是）。由于红点现在受到障碍物影响，依赖于红点的那部分结点也一样被影响了，G值是不准确的。（但是没有立刻被更新）

上图中红点受障碍物直接影响，EdgeCost减少为1，Rhs更新为5(=4+1)，之后随着Dequeue，会先更新红点的G值(G=Rhs=5)，然后向前传递，左边点的G值也会被陆续更新，因此我们可以获得准确的G值与Rhs值

2.2.当障碍物出现时：

       如2.1所述，G<G(红点)的G值仍然是正确的，而G>G(红点)的部分结点依赖于红点，比如左边三个白点。
       由于障碍物出现，图中的EdgeCost由2增加到5
注意： 例子中的S2，由于通道的单向性，红点仅是它的predecessor，固它的G不依赖于红点。而且S2中的改变与当前的讨论无关，在此可以暂时忽略

        此时根据我们的算法，对红点Dequeue会使这个结点处于Underconsistent状态，即设置G=∞（类似于重置到初始状态），随着Dequeue继续进行，会把所有受牵连的结点，都设置为G=∞。之后如果再有影响传递到这些结点，那么一定是从连通至终点的路径传来的影响（比如其实这个例子中，红点最后会受到S2结点的影响而更新正确的G值，后面会进一步解释这个例子），此时就如同第一次计算时的情况一样，可以获得准确的G和Rhs

定义H（S到起点启发值）：

$h(s,s_{start})$

定义Key（非完全）：

$Key \ = \ \ \ <min[g(s),rhs(s)]+h(s,s_{start}),\quad min[g(s),rhs(s)]>$

可以看到Key值由两个元素组成。
Key值是用来示意先处理谁的量，我们希望越有可能成为最终最短路径的点越先处理。
因此第一个值是结点G或Rhs的较小值+S到起点的启发值。
$\begin{aligned} &min[g(s),rhs(s)]& \quad示意S到终点的距离 \\ &h(s,s_{start})&\quad 示意S到起点的距离 \end{aligned}$

当这个值相加越小时，我们可判断S为终点到起点路程更短的点（Sgoal→S→Sstart越趋近于Sgoal→Sstart两点的直线距离）
然而这个和会有很多重复，因此我们还定义了第二个值辅助判断：单纯S到终点的距离

比较原则：先由Key中第一个元素决定Key大小，仅当第一个元素相等时再由第二个元素决定大小

因为该值越小意味着该结点为较短路径的一部分。
因此为了寻找最短路径，我们可以统一地使用Key值越小，越优先处理的原则。

上述Key值定义的一个问题：

        由h值的定义，h与“S到起点的距离”有关。那么问题来了，我们的Sstart是会随着机器人移动而改变的（Sstart永远是机器人当前位置），那么就意味着这个Key中的H值也需要随之改变了，但我们之前已经计算出来的Key值用的还是旧的H值，怎么办呢？
        根据机器人的行动远离或接近终点，新旧h值分别相差±Δh。
$\Delta h = h(s_{last},s_{start}),\ s_{last}为上一个s_{start}点$

        比如机器人朝着终点行进一步，那么对于之前计算过的所有处于机器人前方的结点的Key都要相应减少一个Δh：
$Key_{updated} \ = \ \ \ <min[g(s),rhs(s)]+h(s,s_{last})-\Delta h,\quad min[g(s),rhs(s)]>\\注意在机器人移动后，对于计算过的旧Key，在计算时的s_{start}已经变成s_{last}了\\ （值无变化，但是意味着过时了）$

        然而这是非常痛苦的，设想我们有10000个计算过的Key，当我们机器人移动一次的时候，我们就要重新计算10000个Key……

解决策略：

        说到底我们只是想：已经计算过的Key和接下来将计算的新Key具有可比性罢了（为了选出最小的key，方便我们决定结点的处理顺序）既然如此，与其对10000个已存在的Key值减Δh，为何不增加新计算Key值加Δh呢？对10000个旧Key-Δh或对新加入的一个Key+Δh，这样的排序结果是一样的。

该策略存在的瑕疵：

       想必已经有很多人想到，上述情况中，对于靠近终点的结点而言确实需要-Δh，但是对于那些在机器人前进方向之后的结点，这个启发值应该+Δh，相差一个负号，这样笼统的一刀切，是不是不太好呢？

对此，一个解决方法是：求出Δh的代数值而非绝对值，但这有点难度，因此没采取这种方法。

这里用的第二个解决方法是：妥协，虽然存在这个小瑕疵，但它带来的效果远比重新计算10000个Key值划算，而且符号相反的情况不总是发生。这相当于是牺牲了部分启发准确性换来了效率，是值得的。所以下面……

定义Km(KeyModifier)：

$K_m=\left\{ \begin{aligned} &0&&, if(s_{last} == null) &\\ &K_m + h(s_{last},s_{start})&&,When\ robot\ moves& \end{aligned} \right.$

这就是上述的用来解决Key存在问题的Δh，由于机器人会移动多次，所以多个Δh累加我们定义为Km

定义Key（最终）：

$Key \ = \ \ \ <min[g(s),rhs(s)]+h(s,s_{start})+K_m,\quad min[g(s),rhs(s)]>$
这个Key值被Km修饰后比之前更加合理

定义PriorityQueue（优先队列U）：

$U \ = \{(Key_1,s_i>),(Key_2,s_j)...(Key_n,s_k)\} ,\ (Key_1<Key_2<...<Key_n)$

其中结点S是该Key所对应的结点，结点之间没有必然联系，但不重复；U的排列只通过Key决定。
这是我们检测结点顺序的标准，也就是说假设U一直保持这个顺序，那我们会先检测Si，然后是Sj，最后Sk。我们之前也说过，检测一个结点意味着会改变它的数值。

Dequeue过程：

这里将举一个例子形象说明Key是如何进入Queue中，Queue又是如何被Dequeue的。
整个寻路过程事实上就是多次Dequeue的结果。
还是刚刚的例子，不过此时我们需要考虑S2了：

如下图，和之前一样我们模拟障碍物出现，把EdgeCost从2改变为5，此时红点的Rhs受到影响更变为10,。同时S2由于环境影响（图中没有示意这个影响是如何造成的），结果导致S2的Rhs值降低了1。
受环境直接影响的点我们会进行状态判定，由于S1和S2都不处于Consistent状态，所以我们会把它们加入队列中，这意味着S1和S2此时都需要计算Key值并入列：
$U \ = \{(<11,7>,s_1),(<12,8>,s_2)...(其它可能存在结点本例中省略)\}$

        根据上面的队列结果，我们会优先Dequeue最小Key值的元素（即第一个，S1）。所以我们立刻将它取出队列，并进行状态判定： 结果为Underconsistent。
        所以我们立刻执行三部曲：

• g=∞

• 传递到所有predecessor（左边三个白点）
  （事实上对于处于非稳定状态的predecessor我们也会把它加入队列，不过本例忽略）

• 将该结点S1再次加入队列中，如下图：
  $U \ = \{(<12,8>,s_2),(<14,10>,s_1)...(其它可能存在结点本例中省略)\}$

算法继续进行Dequeue过程，这次轮到S2，由于G=Rhs，为Consistent状态，于是不再加入队列。
由于这是D*Lite第二个版本，所以会检测S2是否为S1的更好successor，结果是肯定的，因此算法会先把S1的Rhs由10更新为9，然后更新在队列中的Key值
$U \ = \{(<13,9>,s_1)...(其它可能存在结点本例中省略)\}$

最后DequeueS1，S1的G值最后被设置成9，处于稳定状态 这例子事实上也演示了障碍物出现后的寻路是如何得到正确的G值与Rhs值的。 此时S1的G值是由S2传递过来的。而S2的影响也绝对是从连通路径传递过来的（因为除了出现障碍物的结点可以传递影响以外，就只有从终点连通处传来了）

Dequeue过程就是如此，一步步地取出U中的Key，不断对结点进行更新，直到找到最终路径

四、整体框架

       前面穿插着讲了不少算法的原理，其实已经解释完算法的核心了。但比较散乱，听着容易一头雾水。在这一节会对整个算法的流程做一个简述，帮助理解算法。

1.初始化

设置Km=0
设置所有结点G=∞
设置终点的Rhs=0，其余结点Rhs=∞
清空队列U（就是Queue）
把终点加入队列U

2.首次寻路

寻路过程事实上就是不断Dequeue的过程
先对终点Dequeue，G=Rhs=0
传递到predecessor
predecessor受终点传递影响
predecessorRhs更新为从终点计算（因为自身Rhs=∞，而终点传来Rhs=G(Sgoal)+Cost(Sgoal,S)更小）
predecessor加入队列

对predecessor进行Dequeue
设置它们的G值
继续向前传递
……

直到达到寻路结束的标准（详见后面的伪代码）

如果最终起点G=∞则没有路径
否则贪婪地从起点开始，根据最小G值一直检索，直到G=0则可获得最短路径

3.Robot行走

检测环境的障碍物改变……
如果环境不改变则保持原路径行走

4.检测到障碍物改变

更新Km：Km +=h(Slast,Sstart)
更新EdgeCost
对EdgeCost改变的点寻找更好的Rhs
对EdgeCost改变的点，进行结点检测（UpdateVertex）

如果处于非Consistent状态，则加入队列U
继续对U进行Dequeue
直到再次达到寻路结束的标准

五、伪代码&解析

这一部分将会着重关注这些功能到底是如何一步步实现的

procedure CalculateKey(s)

$\{01’\}return [min(g(s), rhs(s)) + h(s_{start},s)+km; min(g(s), rhs(s))];$

procedure Initialize()

$\{02’\}U = ∅;$
$\{03’\}km = 0;$
$\{04’\}for\ all\ s ∈ S,\ \ rhs (s)=g(s)=∞;$
$\{05’\}rhs(s_{goal})=0;$
$\{06’\}U.Insert(s_{goal}, CalculateKey(s_{goal}));$

procedure UpdateVertex(u)

$\{07’\}if (g(u) \neq rhs(u)\ AND\ u ∈ U) U.Update(u, CalculateKey(u));$
$\{08’\}else\ if (g(u) \neq rhs(u)\ AND\ u \notin U) U.Insert(u, CalculateKey(u));$
$\{09’\}else\ if (g(u)=rhs(u)\ AND\ u ∈ U) U.Remove(u);$

如果处于非Consistent状态，则把结点插入U（或原来已在U的则更新）
如果处于Consistent状态，则把存在U中的结点移除

procedure ComputeShortestPath()

$\{10’\}while (U.TopKey() <CalculateKey(s_{start})\ OR\ rhs(s_{start}) > g (s_{start}))$

$\{11’\}\quad u = U.Top();\quad \textbf{ //开始一次Dequeue}$
$\{12’\}\quad k_{old} = U.TopKey();$
$\{13’\}\quad k_{new} = CalculateKey(u));$

$\{14’\}\quad if(k_{old}<k_{new})\quad \textbf{ //先看看该结点Key值是否需要更新}$
$\{15’\}\quad \quad U.Update(u, k_{new});\quad \textbf{ //是则直接更新结点在U中位置并进入下一循环}$

$\{16’\}\quad else\ if (g(u) > rhs (u))\quad \textbf{ //局部过一致}$
$\{17’\}\quad\quad g(u)=rhs(u);$
$\{18’\}\quad\quad U.Remove(u);$
$\{19’\}\quad\quad for\ all\ s ∈ Pred(u) \textbf{ //对u的所有predecessor}$
$\{20’\}\quad\quad\quad if (s \neq s_{goal}) \\ \quad\quad \quad\quad \quad\quad \quad rhs(s) = min(rhs(s),c(s, u)+g(u));\textbf{ //如果u是更好的successor则更改predecessor的Rhs}$
$\{21’\}\quad\quad\quad UpdateVertex(s);$

$\{22’\}\quad else\quad \textbf{ //局部欠一致}$
$\{23’\}\quad\quad g_{old} = g(u);$
$\{24’\}\quad\quad g(u)=∞;$
$\{25’\}\quad\quad for\ all\ s ∈ Pred(u) ∪{u}\quad \textbf{ //检测所有predecessor和自己}$
$\{26’\}\quad\quad\quad if (rhs(s)=c(s, u)+g_{old})\textbf{ //这意味着u曾是最好结点，但如今u堵塞了}$
$\{27’\}\quad\quad\quad\quad if (s \neq s_{goal}) rhs(s) = min_{s'∈Succ(s)}(c(s, s')+g(s')); \textbf{ //为s找新的最优结点}$
$\{28’\}\quad\quad\quad UpdateVertex(s);$

关于Dequeue循环终止的条件：

1. 起点要达到Consistent状态
2. 队列中最小Key值小于起点的潜在Key值（即使起点不在队列中事实上我们也能为它计算Key）
   Key值越小意味着越接近终点。而队列中Key比起点Key要大，说明它们比起点更远离终点，所以它们在绕远路，没有必要对它们进行Dequeue了

procedure Main()

$\{29’\}s_{last} = s_{start};$
$\{30’\}Initialize();$
$\{31’\}ComputeShortestPath();$
$\{32’\}while (s_{start} \neq s_{goal});$
$\{33’\}\quad /* i如果g(s_{start})==∞，则没有路径 */$
$\{34’\}\quad s_{start} = arg min_{s'∈Succ(s_{start})}(c(s_{start},s')+g(s'));\quad \textbf{ //贪婪地选最佳结点}$
$\{35’\}\quad Move\ to\ s_{start};\quad \textbf{ //机器人移动}$

$\{36’\}\quad Scan\ graph\ for\ changed\ edge\ costs;\quad \textbf{ //检测中途障碍物改变}$
$\{37’\}\quad if\ any\ edge\ costs\ changed$
$\{38’\}\quad\quad k_{m} = k_{m} + h(s_{last},s_{start});\quad\textbf{ //计算Km}$
$\{39’\}\quad\quad s_{last} = s_{start};$
$\{40’\}\quad\quad for\ all\ directed\ edges (u, v) with\ changed\ edge\ costs \textbf{ //对所有直接影响的结点}$
$\{41’\}\quad\quad\quad cold = c(u, v);\quad \textbf{ //记录之前的花费}$
$\{42’\}\quad\quad\quad Update\ the\ edge\ cost\ c(u, v);$

$\{43’\}\quad\quad\quad if (c_{old} >c (u, v)) \quad \textbf{//如果是障碍物消失}$
$\{44’\}\quad\quad\quad\quad if (u \neq s_{goal})\\\quad\quad\quad\quad\quad\quad\quad\ \ rhs(u) = min(rhs(u),c(u, v)+g(v));\quad \textbf{//结点更好则取代}$

$\{45’\}\quad\quad\quad else\ if (rhs(u)=c_{old} + g(v))\quad \quad \textbf{//如果是障碍物出现，判断结点v在以前是否为u的最佳successor}$
$\{46’\}\quad\quad\quad\quad if (u \neq _{goal})\quad \textbf{//如果是且非终点，则为u寻找新的successor}\\ \quad\quad\quad\quad\quad\quad\quad\ \ rhs(u) = min_{s'∈Succ(u)}(c(u, s')+g(s'));$
$\{47’\}\quad\quad\quad UpdateVertex(u);$
$\{48’\}\quad\quad ComputeShortestPath();\quad \textbf{//重新计算路径}$

六、例子

首先设定所有EdgeCost值（显示在路径旁，注意右下的通道花费为10），另外图中均为双向通道。
然后设定每个结点的H值（显示在圆圈中），这里是用s到起点前之间的结点数作为启发值H
为了方便表述，这里先给他们个编号：
在目前状态下：
h=0的点为A
h=1的点为B
h=2，靠上的点为C
h=2，靠下的点为D
h=3的点为E

初始化，终点以Key<3.0>加入队列

Dequeue终点，向predecessor传递。
首先更新predecessor的Rhs
然后predecessor都处于Overconsistent状态，加入队列

Dequeue C
由于该结点处于Overconsistent状态，所以g=rhs
向所有predecessor传递，终点不会变动
此时对B，D点立刻检测rhs值
由于C是更好的successor，所以B，D的rhs都变成了2
此时对D由于已在队列中，我们则更新它在队列中的Key值以改变队列顺序
对于B我们则把它加入到队列中

Dequeue B
设置B的G=2，向predecessor传递
此时对于C，由于B→C的新Rhs＞原来的Rhs1，B并不是C更好的successor，因此Rhs保持不变
而且C点处于稳定状态，也不需加入到队列中
此时对D也一样，由于B→D的新Rhs＞原来Rhs2，而且它本来已经在队列中，所以不用管
对于A点则常规操作并加入队列

Dequeue A
然后我们已经可以找到合适的路了，于是Robot向前走了一步
（这里可以看到我们基本没去管D，这是D*Lite节省性能的体现）
由于起点改变，我们更新了所有的h值
Km也要增加

此时C点出现了障碍
它的EdgeCost立刻被设置为∞

并且相应的，我们会更新C点的Rhs
由于所有EdgeCost都是∞，所以Rhs也被设为∞
随即由于Underconsistent C点被加入队列中

在这里被EdgeCost直接影响的结点还有B D E，我们也需要对它们更新Rhs与UpdateVertex()
由于E是终点所以它雷打不动
然后对于B和D都会去找一个更好的successor
然后很明显B找到更好successor是A
而D找的更好successor是B
这是完全找错了，这里体现了这个算法的一些无效运算
不过这种情况其实并不常见（嗯，视频里面是这么说的）

于是对B D更新Rhs并更新队列

接着Dequeue C
这里会把它设置g=∞
然后由于它现在处于Consistent（是的，双∞也算），所以不需要再加入队列。

然后Dequeue B
B也处于Underconsistent状态，设置为∞（事实上就是一次G值重置）
然后传递到所有predecessor。
为它们改变Rhs值从而找一个更好的successor，于是造成下图改变

这里省略几波Dequeue过程
最终起点处于稳定状态
Robot得以继续移动
Km增加
重新计算h

当Robot移动到D点时，障碍物移动到B点了
此时还是更新EdgeCost先

然后对于受EdgeCost直接影响的A B C D
B的Rhs=∞，A的Rhs也无法选择地= ∞，C的Rhs=1（意味着C→E是最好的）
而D的Rhs仍为10（因为它使用的是过时的G值判断，它仍认为E点是最好的而不是D，但没有关系，在必要时它会被更新成正确的数值的）

几波Dequeue后，又出现了连通的道路
此时我们根据算法的循环控制条件，其实已经不需要管B点了
因为B的Key大于Sstart目前的潜在key（<4,2>）（虽然它不在队列，但我们也可以把它的Key算出来用作参考）
这意味着B比起点更远离终点（因为越靠近终点Key越小），所以我们没有必要对它Dequeue了

最后一波移动
障碍物又进行了一波走位
更新了EdgeCost，和相关的Rhs和Key
但我们不需要Dequeue任何东西了，因为还是刚刚的说法（这次也打在图上了）
所有的Key都比Sstart的Key要大，说明它们绕远路了。

至此我们就已经找到完整道路了。
虽然在一个小例子中D*Lite显得很蠢，
但是在大的未知环境下还是很有用的。

七、主要源码

文章太长了，还是新开一个帖子放吧：
D*Lite部分源码

八、Unity完整演示项目

纯演示预览：

下载地址
D*Lite演示预览

截图：

Unity完整项目：

D*Lite算法 Unity 2019.3.4项目文件

• 注意下载前留意Unity版本号不能过低
• 直接在Unity中运行效率会比Build完后低，所以里面的时间显示仅供参考（而且这不代表是整个算法的完整执行时间，只是Dequeue过程的时间，甚至不包括循环间隔（看源码里面的几个stopwatch就知道了））
• 在这个项目我事实上做了一些变通，Km和H的计算方式没有完全依据算法，另外注释掉了一些感觉用不上的过程
• 还有队列的储存方式为了贪方便只是用了个单向链表，查找时还是很慢的，如果改变储存方式其实能有进一步提升

九、尾声

虽然一篇文章可能还不足以弄懂这个算法，而且这篇文章写的也比较杂乱，但还是希望这可以带来一些启示
然后我也只是一个初学者，文中对算法的部分理解可能有误，还请理解并指出（没错，这么多年的码龄都是假的，估计这是我小学阴差阳错注册的号（但没想到最后还是打算走这条路（滑稽））