计算示例——递归与迭代

题目源于SICP。

第一题

python实现

# recursive process
def f(n):
	if n < 3:
		return n
	else:
		return f(n-1) + 2*f(n-2) + 3*f(n-3)

# iterative process
def f(n):
	if n < 0:
		return n
	else:
		a, b, c = 0, 1, 2
		for i in range(n):
			a, b, c = b, c, 3*a + 2*b + c
		return a

scheme实现

递归版本

(define (f n)
  (cond ((< n 3) n)
        (else (+ (* 3 (f (- n 3)))
                 (* 2 (f (- n 2)))
                 (f (- n 1))))))

迭代版本

(define (f-iter a b c n)
  (cond ((< n 0) n)
        ((= n 0) a)
        (else (f-iter b c (+ (* 3 a)
                        (* 2 b)
                        c)
                 (- n 1)))))

(define (f n)
  (f-iter 0 1 2 n))

用python实现一个计算过程实在太接近人类的思考过程了。简直就像是数学定义重新写一遍。所以先用python实现，然后再写其他语言实现使非常方便的。

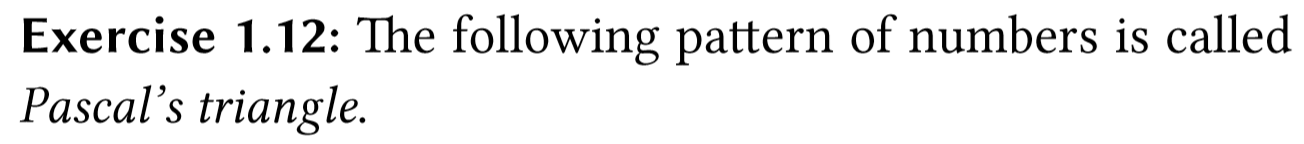
python实现

def pascalTriangle(r, c):
	if r < c or c <= 0:
		raise Exception
	elif r == c or c == 1:
		return 1
	else:
		return pascalTriangle(r-1, c-1) + pascalTriangle(r-1, c)

scheme实现

(define (pascal-triangle r c)
  (cond ((or (= r c) (= c 1)) 1)
        ((or (< r c) (< c 0) (= c 0)) -1)
        (else (+ (pascal-triangle (- r 1) (- c 1))
                 (pascal-triangle (- r 1) c)))))

首先，Fibonacci numbers的实现如下
python实现

# recursive process
def fib(n):
	if n == 0:
		return 0
	elif n == 1:
		return 1
	else:
		return fib(n-1) + fib(n-2)
#iterative process
def fib(n):
	a, b = 0, 1
	for i in range(n):
		a, b = b, a+b
	return a

scheme实现

recursive process

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

iterative process

(define (fib n)
  (define (fib-iter a b count)
    (cond ((= count 0) a)
          (else (fib-iter b (+ a b) (- count 1)))))
  (fib-iter 0 1 n))

首先证明： $Fib(n) = (\varphi ^n-\psi ^n)/\sqrt{5}$
当 $n=0$
$(\varphi ^0-\psi ^0)/\sqrt{5}=Fib(0)=0$
当 $n=1$
$(\varphi ^1-\psi ^1)/\sqrt{5}=(\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2})/\sqrt{5}=Fib(1)=1$
命题成立。
假设 $n=k-2$ 和 $n=k-1$ 时，命题成立。则 $n=k$ 时，有
$Fib(k)=Fib(k-1)+Fib(k-2)=\left [(\varphi ^{k-1}-\psi ^{k-1})+(\varphi ^{k-2}-\psi ^{k-2}) \right ]/\sqrt(5)=(\varphi ^{k-2}(1+\varphi)-\psi ^{k-2}(1+\psi ))/\sqrt(5)$
其中
$1+\varphi=1+\frac{1+\sqrt{5}}{2}=\frac{3+\sqrt{5}}{2}=(\frac{1+\sqrt{5}}{2})^2=\varphi^2$
同理，可证
$1+\psi=\psi^2$
因此，有
$Fib(k) = (\varphi ^k-\psi ^k)/\sqrt{5}$
故，命题得证。

要证 $Fib(n)$是最接近 $\varphi^n/\sqrt(5)$的整数，即证
$|Fib(n)-\varphi^n/\sqrt(5)|<\frac{1}{2}$
其中
$|Fib(n)-\varphi^n/\sqrt(5)|=|\psi^n/\sqrt(5)|=|\psi|^n/\sqrt(5)$
因为， $|\psi|=|\frac{1-\sqrt{5}}{2}|$，所以 $0<|\psi|<1$
$|\psi|^n/\sqrt(5)<1/\sqrt(5)<\frac{1}{2}$
故命题得证。