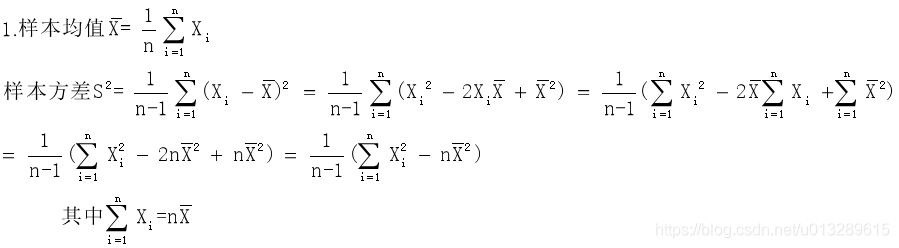1.原函数和变限积分的区别:
如果一个函数是连续的,那么∫f(x)dx和∫(a,x)f(x)dx区别不大,后者属于前者的一部分,前者是原函数,包括多个,后者是变限积分只是一个函数,这里a是常数。
如果函数存在间断点那么情况就不一样了,着重讨论第一类间断点:
自然原函数是不存在的了,可是变限积分是存在的,试想一下如果一个函数存在有限个第一类间断点,那么定积分在一定区间是肯定存在的,变限积分也就是将定积分的上限不固定,所以变限积分存在。
假如x0是f(x)第一类间断点,那么∫(a,x0+Δx)f(x)dx-∫(a,x0)f(x)dx=∫(x0,x0+Δx)f(x)dx,当Δx趋近0,那么它也趋近0,所以函数在该点是连续的。讨论可导:
(∫(a,x0+Δx)f(x)dx-∫(a,x0)f(x)dx)/
Δx=∫(x0,x0+Δx)f(x)dx/
Δx=f(ξ)(利用积分中值定理)
,Δx大于0时若趋近0,那么右导数为f(x0+) ,同理左导数f(x0-).
由此看来,如果是可去间断点,那么变限函数必也可导,如果是跳跃间断点,那么变限积分只连续不可导。
综上所述,原函数和变限积分区别还是很大的。
2.极限可拆问题
1、拆成或加、或减时,只要拆开后的两项或多项,各自的极限存在,
也就是说各自的极限没有无穷大的情形,就大胆的拆,没有问题。
2、如果拆开成加、减时,只有一项出项无穷大的情形,也没有问题。
3、若拆开成加、减时,有两项,或多项出现无穷大时,就不可以拆。
4、若以因式的方法拆成乘、除时,其实就是因式分解,只要拆出来的因子factor不是无穷大,就没有问题。
要注意的是:因式必须是整体的因子,而不是局部的因式。
3.等价、合同、相似的联系与区别。
等价,秩相等即为等价,而相似、合同秩必相等。因此,合同、相似包含等价。等价是最弱的。
相似,特征值相同即为相似。
合同,不一定对对称矩阵而言(定义上不要求被作用的矩阵对称),只要左边作用一个可逆矩阵的转置,右边作用该可逆矩阵,所得的矩阵即与原矩阵合同。
当然,一般是对对称矩阵作用,所以下面只讨论对称矩阵的合同与相似。
合同等价于正负惯性指数相同,正负惯性指数的符号即为特征值的符号。
于是,对称矩阵相似即合同(相似的特征值相同,正负号一定也相同,所以一定程度上可以认为相似比合同严格)。合同不一定相似(即使对对称矩阵而言),仅仅当用正交矩阵作用时,合同才与相似一致。
所以,对对称矩阵而言,相似=>合同=>等价。
对一般矩阵而言,相似和合同无必然联系(即相似不一定合同,因为相似变换矩阵不一定正交;合同不一定相似,也是因为合同变换矩阵不一定正交),但都能推出等价。
4.可交换矩阵的充分条件:
(1) 设A , B 至少有一个为零矩阵,则A , B 可交换;
(2) 设A , B 至少有一个为单位矩阵, 则A , B可交换;
(3) 设A , B 至少有一个为数量矩阵, 则A , B可交换;
(4) 设A , B 均为对角矩阵,则A , B 可交换;
(5) 设A , B 均为准对角矩阵(准对角矩阵是分块矩阵概念下的一种矩阵。即除去主对角线上分块矩阵不为零矩阵外,其余分块矩阵均为零矩阵),则A , B 可交换;
(6) 设A是A 的伴随矩阵,则A与A可交换;
(7) 设A可逆,则A 与其逆矩阵可交换;
注:A的逆矩阵经过数乘变换所得到的矩阵也可以与A进行交换。
(8)A^n(n=0,1…, )可与A^m(m=0,1…, )交换.这一点由矩阵乘法的结合律证明。
定理2
(1) 设AB =αA +βB ,其中α,β为非零实数,则A , B 可交换;
(2) 设A m +αAB = E ,其中m 为正整数,α为非零实数,则A , B 可交换.
定理3
(1) 设A 可逆,若AB = O 或A = AB或A = BA ,则A , B 可交换;
(2) 设A , B 均可逆, 若对任意实数k , 均有A = ( A - k·E) B ,则A , B 可交换.
5.f’(x)与[f(x)]’区别
对于求导最重要的是搞清楚自变量和因变量可以假设z=f(y),而y是x的函数,即y=g(x),那么就可以很清楚的解决了f’(y)=dz/dy,而[f(y)]‘则是对复合函数求导,用链式法则,即先对z求导,再对y求导,也就是[f(y)]’=dz/dy×dy/dx
6.几个常见的超越积分(不可积积分)
1.∫e(ax2)dx(a≠0)
2.∫(sinx)/xdx
3.∫(cosx)/xdx
4.∫sin(x^2)dx
5.∫cos(x^2)dx
6.∫x^n/lnxdx(n≠-1)
7.∫lnx/(x+a)dx(a≠0)
8.∫(sinx)^zdx(z不是整数)
9.∫dx/√(x^4+a)(a≠0)
10.∫√(1+k(sinx)^2)dx(k≠0,k≠-1)
11.∫dx/√(1+k(sinx)^2)(k≠0,k≠-1)
以后凡是看到以上形式的积分,不要继续尝试,因为以上积分都已经被证明了为不可积积分.但是要注意的是,虽然以上积分的原函数不是初等函数.但并不意味着他们的定积分不可求,对于某些特殊点位置的定积分还是有可能算出来的,只不过不能用牛顿-莱布尼茨公式罢了! 比如∫[0,+∞)e(-x2)dx=√π/2,此处的积分值就是用二重积分和极限夹逼的方法得出的,而且只能算出(-∞,+∞)或是(0,+∞)上的值,其他的值只能用数值方法算出近似值.
7.关于三角函数反函数问题
sinx只在负π/2到π/2定义了反函数,如果x介于π/2到π之间,不能直接用反函数
比如x=π-arcsiny
x介于π/2到π,
那么π-x介于0到π/2了
sinx=sin(π-x)=y
arcsiny=π-x
x=π-arcsiny
8.r(A’A)=r(A)证明
用A’表示A的转置,要证明r(A’A)=r(A),只需证明方程组AX=0和A’AX=0同解.如果AX=0,两边分别左乘A’,得A’AX=0,这说明方程组AX=0的解都是方程组A’AX=0的解;另一方面,如果A’AX=0,两边分别左乘X’,得X’A’AX=0,即(AX)‘AX=0,令Y=AX,则Y’Y=0,注意Y=AX为n维列向量,因此可设Y=(y1,y2,yn)’,则Y’Y=y12+…+yn2=0,因此y1=…yn=0,即Y=AX=0,这说明方程组A’AX=0的解都是方程组AX=0的解,综上我们证明了AX=0和A’AX=0同解,因此r(A’A)=r(A).
9.|A|=0时,|A|=0证明*
用反证法.
假设 |A*|≠0,则A可逆.,由 AA = |A|E = 0
等式两边右乘 A* 的逆矩阵,得 A = 0.
所以 A* = 0
所以 |A*| = 0.这与假设矛盾.
故 当|A|=0时,|A*|=0.
10.卷积公式推导过程
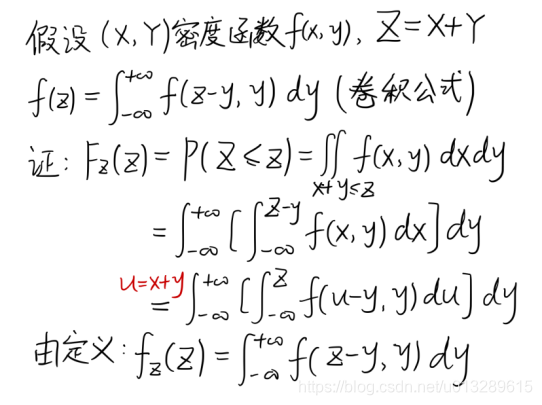
11.样本均值方差问题