信号与系统——初识到理解（第五章——傅立叶变换的应用）

第五章——傅立叶变换的应用

前面我们已经讲解了信号的FS与FT（包括连续与离散情况下），并且给出了常见信号的FT以及FT的性质。接下来，我们简单介绍FT性质的几个主要应用方面。

信号与系统的时频域特性

很自然地，FT的建立为我们提供了一种在频域上考察信号与系统的方法。故而我们首先介绍由FT建立起来的信号与系统的时频域特性。

5.1 傅立叶变换的模和相位表示

我们知道对于一个信号 $f(t)$ ，如果其FT存在，那么将有：

$f(t)\xleftrightarrow {FT} F(\omega)$

而 $F(\omega)$ 写成模和相位的形式为：

$F(\omega)=|F(\omega)|e^{j\angle F(\omega)}$

同样，对于系统的单位脉冲响应 $h(t)$ ，也可以写为：

$H(\omega)=|H(\omega)|e^{j\angle H(\omega)}$

所以，系统通过一个LTI系统的输出可以在频域上表示为：

$Y(\omega)=H(\omega)F(\omega)=|F(\omega)||H(\omega)| e^{j(\angle F(\omega)+\angle H(\omega))}$

可以看出，LTI系统的本质就是对输入信号的幅度和相位做调整。对于输入信号幅度的调整，由其频率响应的幅度完成。对于相位的调整，由其频率响应的相位完成。

5.2 无失真传输系统（讨论连续情况，离散时足以整数约束即可）

所谓失真，是指指信号在传输过程中与原有信号或标准相比所发生偏差的现象。信号经过一个系统后，常见的失真有：

(1) 对于线性系统，有以下两种失真：

a.幅度失真：指输出信号的幅度不符合标准。
b.相位失真：指输出信号的相位不符合标准。

(2) 对于非线性系统，失真还可以是产生了新的频率分量的情况。

那么所谓的不失真，也就是希望系统产生的输出和输入相比变换不大（或者说可以以某一种办法恢复到输入）但也考虑到实际中很难做到完全不变，所以我们对于无失真传输的要求有所放宽，定义为：

如果系统的输出为 $y(t)$,输入为 $x(t)$,且有 $y(t)=Kx(t-t_{0})$,其中K为与时间无关的常数，那么这种传输称为无失真传输，对应的系统称为无失真传输系统。

根据冲激信号的卷积性质，我们可以推出无失真传输系统的另一种刻画方式：

设 $h(t)$ 为系统的单位脉冲响应，如果有 $h(t)=K\delta(t-t_{0})$,则该系统是无失真传输系统。

换做频域上来说：

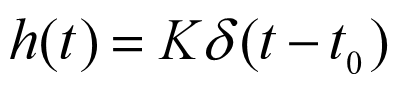
从而有：

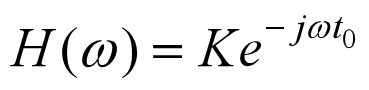
可以得到：

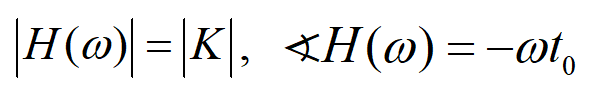
用图像表示也就是：

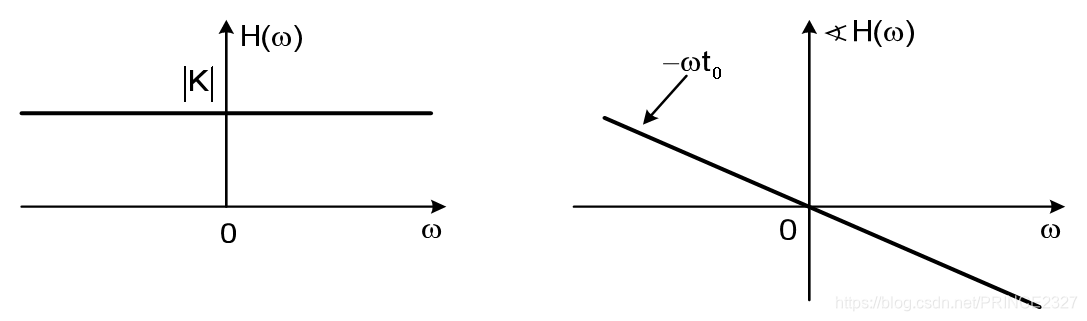
也就是说，无失真传输系统要求系统的幅频特性为恒值，相频响应为线性函数。

可以看出：无失真传输系统本质上就是指对输入信号各分量做恒定的幅度变换和时移操作。

5.3 系统相位

我们知道，LTI系统的频率响应可以写为： $H(\omega)=|H(\omega)|e^{j\angle H(\omega)}$

其中 $\angle H(\omega)$ 就称为系统相位，当 $\angle H(\omega)$ 为关于 $\omega$ 的线性函数时,即 $\angle H(\omega)=\omega\tau_{0}+b$ 时，认为该系统具有线性相位，对应的系统称为线性相位系统，反之，称之为非线性相位系统。

那么这样的规定有什么用呢，下面我们来考察一下它究竟反映了什么。方便起见，我们令b=0，即 ：

$H(\omega)=|H(\omega)|e^{j\omega\tau_{0}}$

对于一个输入信号可以将其在频域上表示为 ：

$F(\omega)=|F(\omega)|e^{j\angle F(\omega)}$

故有：

$Y(\omega)=H(\omega)F(\omega)=F(\omega)|H(\omega)| e^{j\omega\tau_{0}}$

假设其频率响应的幅值为常数K，则转到时域上为：

$y(t)=Kf(t-\tau_{0})$

这也就是前述的无失真传输系统，基于此，我们得到如下结论：

1.无失真传输系统是线性相位系统的一种，幅频响应为恒值的线性相位系统为 无失真传输系统。

2.线性相位系统的本质就是对输入信号的所有分量做相同的时移。

3.非线性相位系统对于输入信号的各个分量做出了不同的时移（也成为色散现象，这里就很形象）。

5.4 群时延

自然地，我们希望找到某一种测度来表示系统对输入信号的延时（在频域上为相移）。故而有群时延的概念：

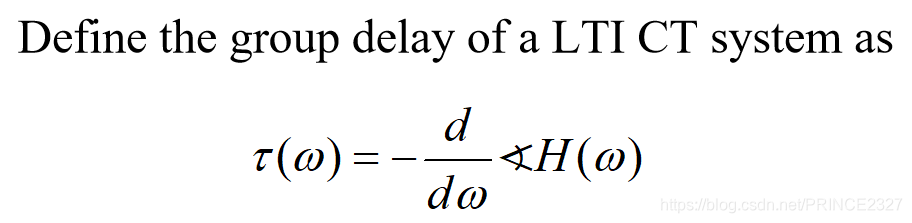
之所以这样定义，是基于FT的时移性质，前面的负号是为抵消时移后在频域上产生的相移前的负号。

群时延反映了系统对输入信号的各个分量的时移情况。

对于线性相位系统，其群延时为常数 $\tau_{0}$ ，这也再次说明了线性相位系统的特性：对输入信号的所有分量做相同的延时。

采样

我们知道，离散时间信号在信号处理中是十分重要的。在信号处理过程中，我们常常接收到一个CT信号，通过将其转换为DT信号做以加工，再将处理过后的DT信号转回为CT信号从而输出。那么该如何得到DT信号呢？其中的一种方法是采样，下面我们来简单介绍。

5.5 通信中对信号的加工

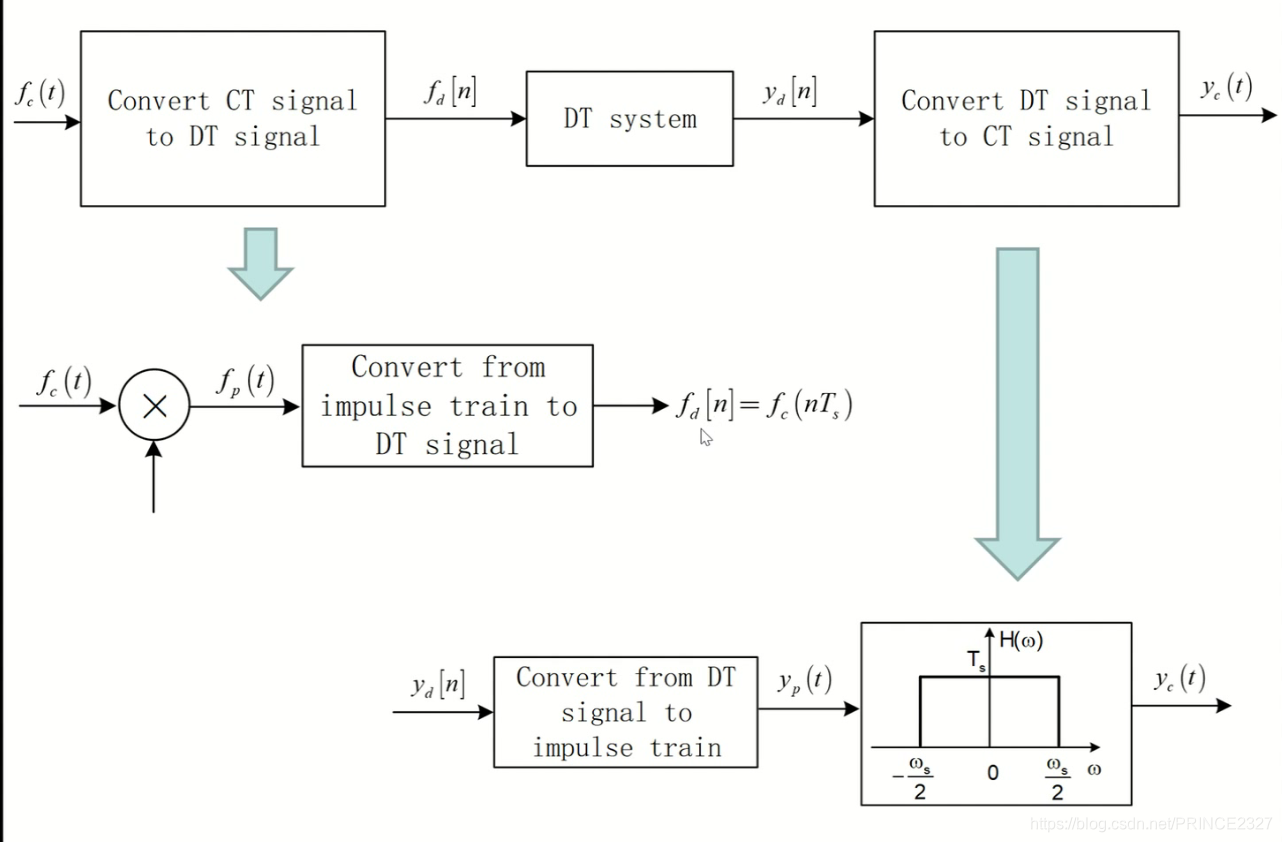
上图就是较为完整地对信号的处理过程。首先接受一个连续信号，通过模数转换器将其转换为数字信号，再通过DT系统得到输出，将输出再通过数模转换器得到最终的输出。下面分别进行介绍。

5.6 冲击串采样

冲激串采样处于模数转换阶段中的第一步。

所谓冲激串采样，即用冲激串信号在时域上进行采样，具体如下：

令 $p(t)=\sum_{l=-\infty}^{l=\infty}\delta(t-lT_{s})$

将其与 $f(t) 相乘有：

$y(t)=f(t)p(t)=f(t)\sum_{l=-\infty}^{l=\infty}\delta(t-lT_{s})=f(lT_{s})\sum_{l=-\infty}^{l=\infty}\delta(t-lT_{s})$

在频域上：

$P(\omega)=\omega_{s}\delta(\omega-k\omega_{s})$

故有：

$Y(\omega)=\frac{1}{2 \pi}P(\omega)*F(\omega)=\frac{w_{s}}{2\pi}\sum_{k=-\infty}^{k=\infty}F(w-kw_{s})=\frac{1}{T_{s}}\sum_{k=-\infty}^{k=\infty}F(w-kw_{s})$

可以看出，时域采样在频域上相当于对于输入信号频谱的调幅和搬移。

用图可表示如下：

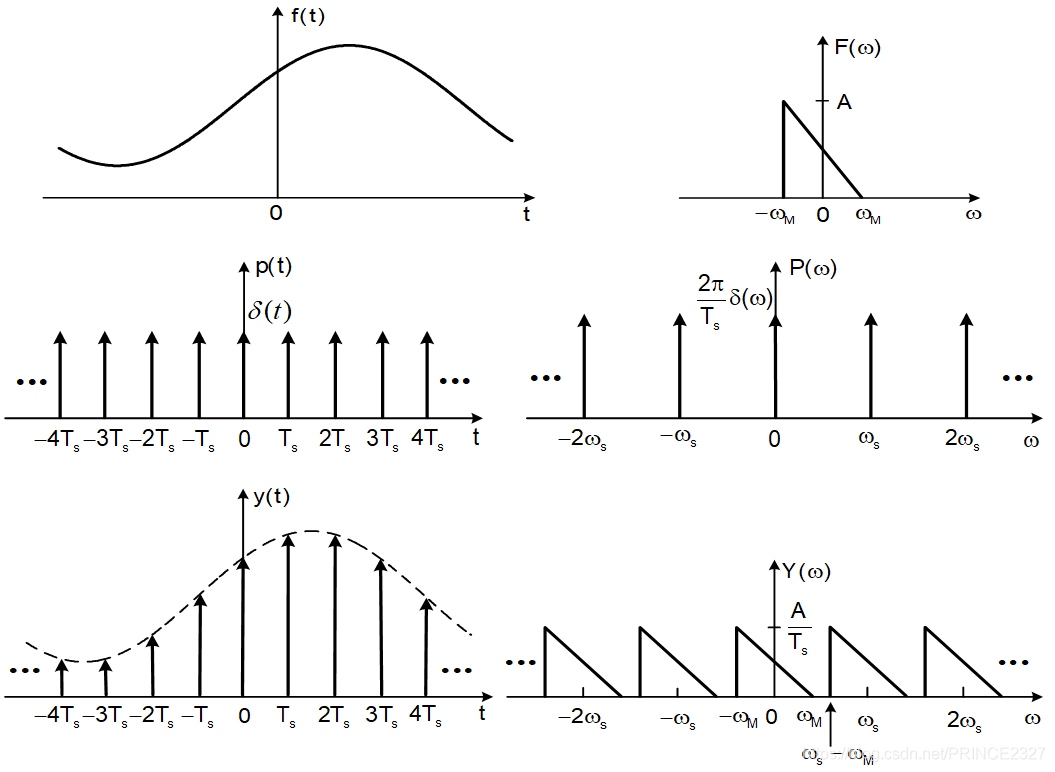
5.7 信号内插

得到了采样信号以后，我们该如何从采样信号中恢复初始信号呢？

在时域上直接恢复似乎显得苍白无力（当然不是你想的把点连起来就行），而在频域上，满足一定条件下（奈奎斯特采样定理），这件事情似乎就显得轻而易举了。

上图中，对于输出频谱 $Y(\omega)$,我们可以通过加一个强度为 $T_{s}$持续适当时间的低通滤波器来恢复输入频谱。

即我们令所加入的滤波器的频率响应为：

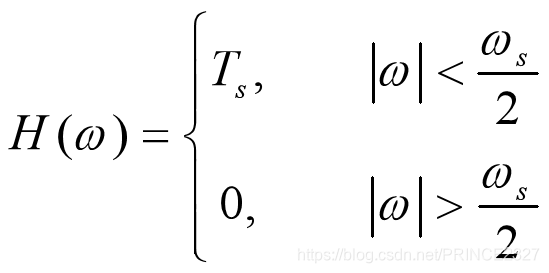
则有：

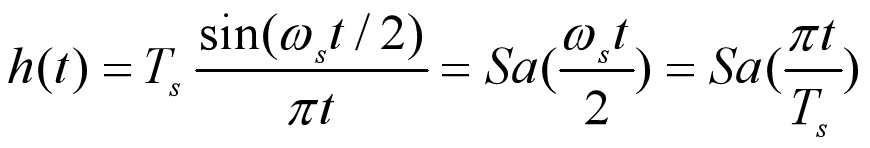
通过该滤波器以后，便可以恢复出输入信号。具体如下图：

频域上的相乘对应与时域卷积，而采样得到的 $y(t)$ 信号是冲激信号，所以卷积后的结果就是将 $h(t)$ 的时域波形以不同的尺度进行等间隔搬移。

公式上可以表示为：


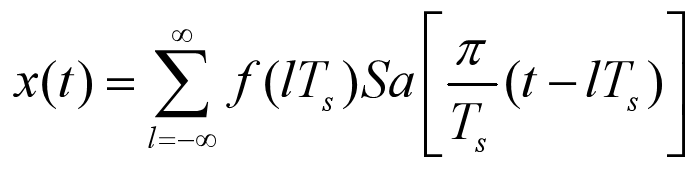
其中

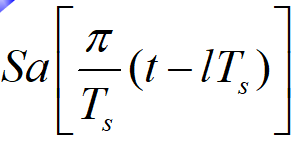
称为内插函数。

可以看出：内插是采样的逆运算。

5.8 奈奎斯特采样定理

从输出恢复输入是有前提的，只有采样信号满足一定约束的条件下，才可以进行信号的内插，下面对此进行考察。

如上图，为采样后信号的频谱。根据上述思路，我们希望加一个滤波器将其还原。上面这种情况当然是可以做到的，但是下图的情况呢？

很明显是不行的，因为搬移后不同中心频率的频谱段混叠起来了，导致频谱的叠加从而使我们无法识别原始信号的频谱，这种现象叫频谱混叠。

避免这种现象也很简单，根据上图坐标，只需要：

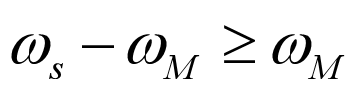
即


其中， $w_{s}$为采样角频率， $w_{m}$为信号带宽， $T_{s}$为采样周期。
这就是奈奎斯特采样定理，对应的 $2w_{m}$即为奈奎斯特率， $w_{m}$称为奈奎斯特频率。

这是与我们直觉相符的：从信息的角度来说，原始信号的信息在采样后有所丢失，只保留了其中的一部分信息。而我们要恢复原始信息，所拥有的信息就不能太少，这也解释了为什么会有奈奎斯特采样定理。

5.9 零阶保持采样

上面说过， 采样完成后我们希望将其转换为一个DT信号，但是采样完后直接得到的信号是冲激串，实际的A/D器件无法在如此短的时间内完成转换，故我们希望将每一个冲激信号的持续时间延长一些（当然这样做后得到的信号就不是冲激信号了），这就是零阶保持电路的作用。

零阶保持电路的时域信号可以表示为：


将其与得到的冲激串信号进行时域卷积（是希望延长持续时间）有：


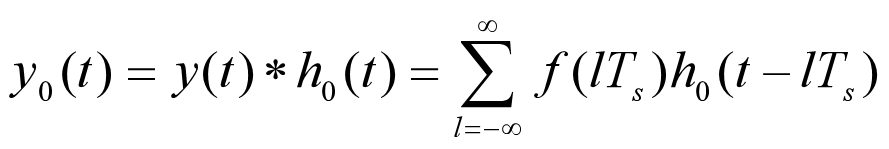
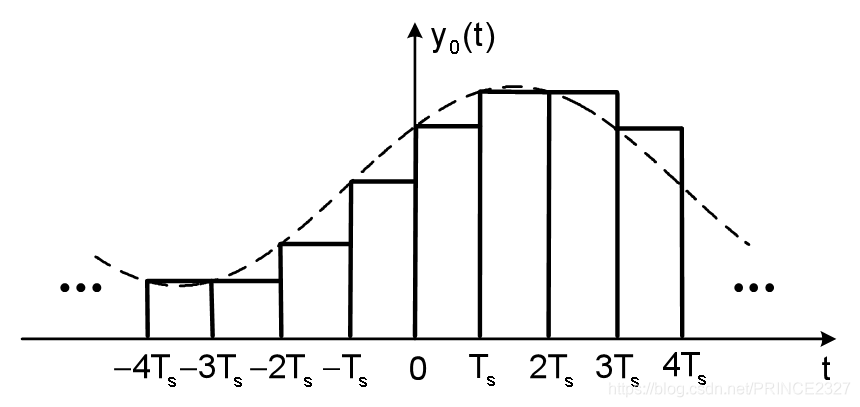
此时，我们便可以延长采样后信号的持续时间从而使其达到A/D转换器的要求。

那么又有了新的问题，零阶保持采样后，我们该如何恢复原信号呢？
我们从频域入手：

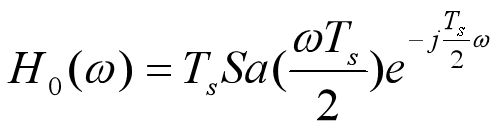
将其与 $y(t)$ 在时域卷积后在频域上可以得到：

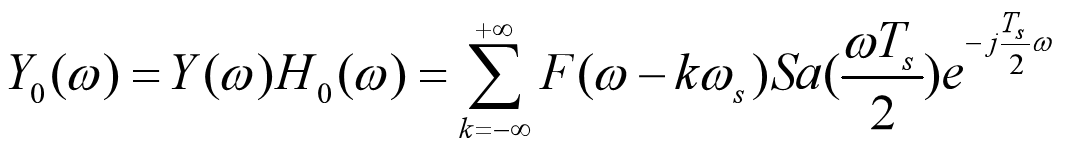
所以我们看到，要恢复原信号，只需构造：

即可。

同样也是一个低通滤波器，其幅频特性和相频特性如下：

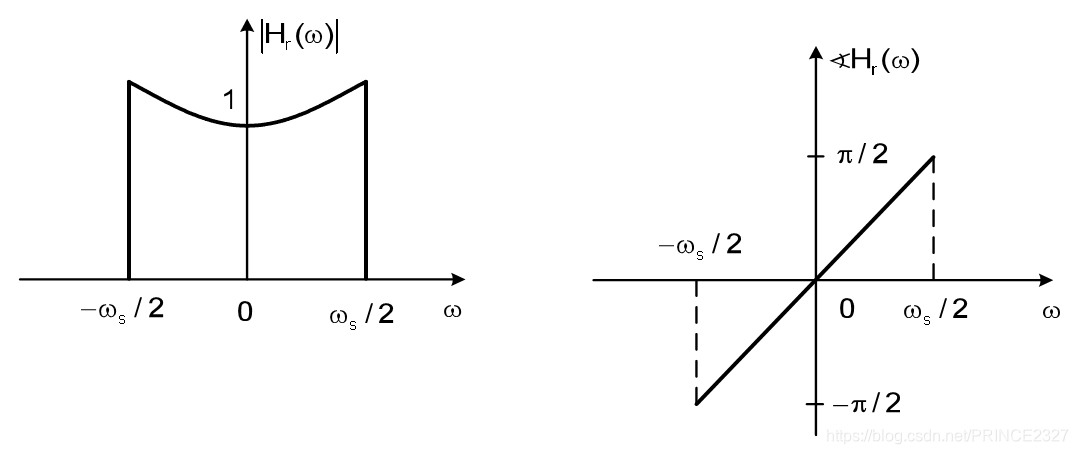
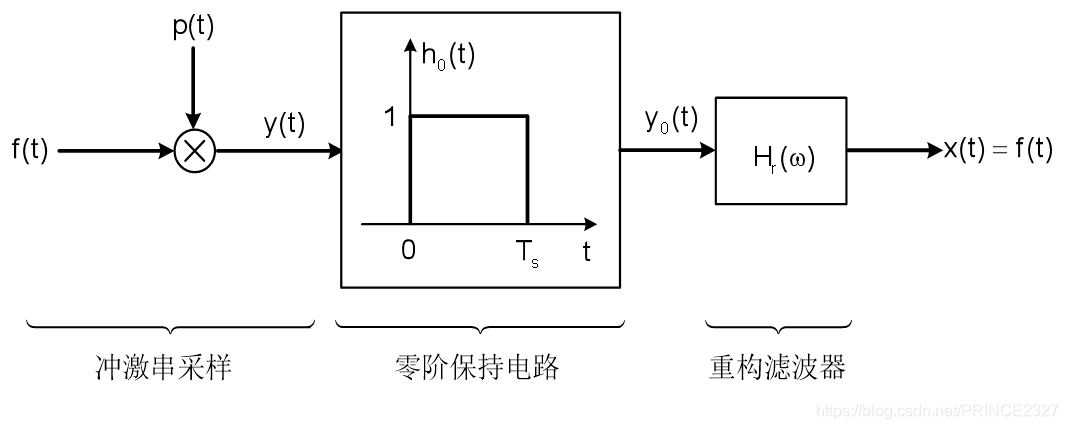
至此，一个完整的信号处理过程中的一个完整阶段如下：

FT在通信中的应用(调制）

除上述之外，FT在通信中也有着应用，主要是信号的调制。

5.10应用（调制）的意义及方法

所谓信号的调制，简单地说就是按某种规则以某种方法去改变输入信号的幅频特性或相频特性。这样做主要有两个目的：

(1) 使信号与信道匹配，比如打电话，总不能背着几千米的天线吧。

(2) 频分复用（据说当年泰坦尼克号沉没就和这个有关）

调制的大致过程如下：

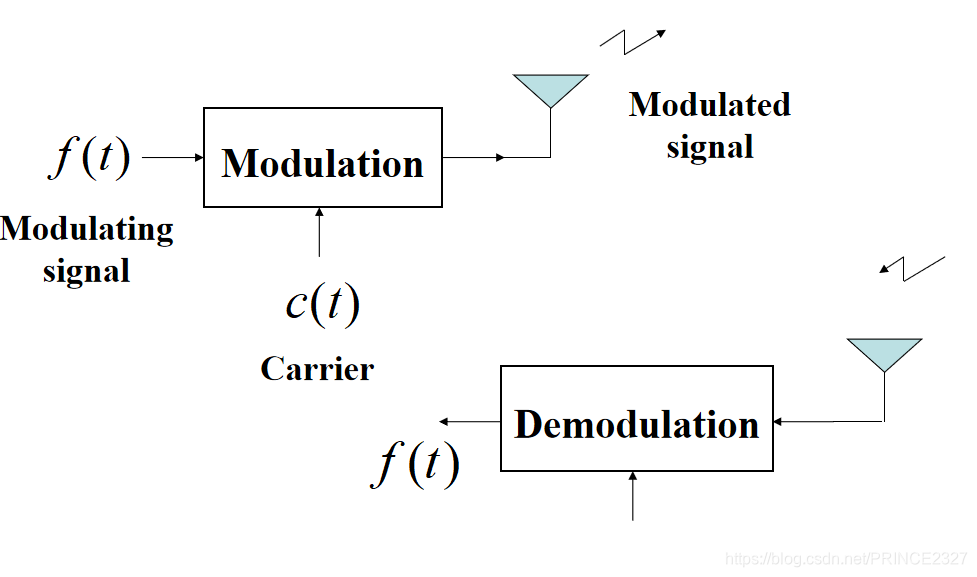
我们给予的输入称为调制信号。
发送端用来改变调制信号的信号称为载波信号。
调制完的输入信号称为已调信号。
接收端解调完的信号称为解调信号。

常常是将一个信号在本地通过某种方法调制，然后辐射出去。接收端接收到后，进行解调，从而使用信号。

调制信号有两种方法：幅度调制和相位调制，这里介绍幅度调制。

5.11 以复指数信号为载波信号的调制

以复指数信号为载波信号对原信号进行调制如下图：

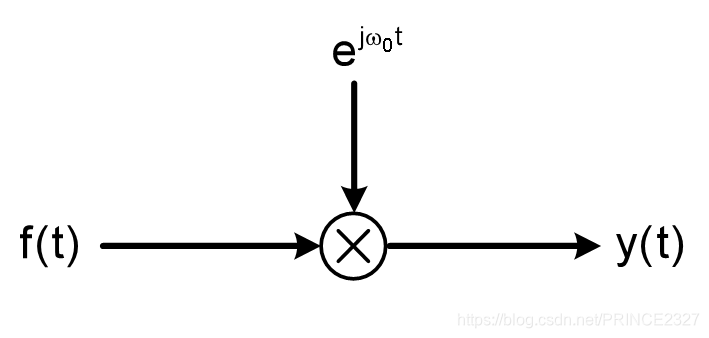
其中载波信号的角频率称为载波角频率。



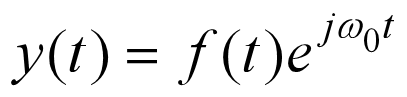
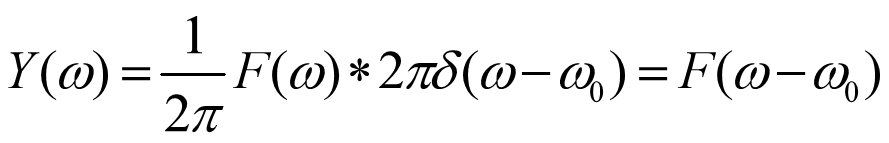
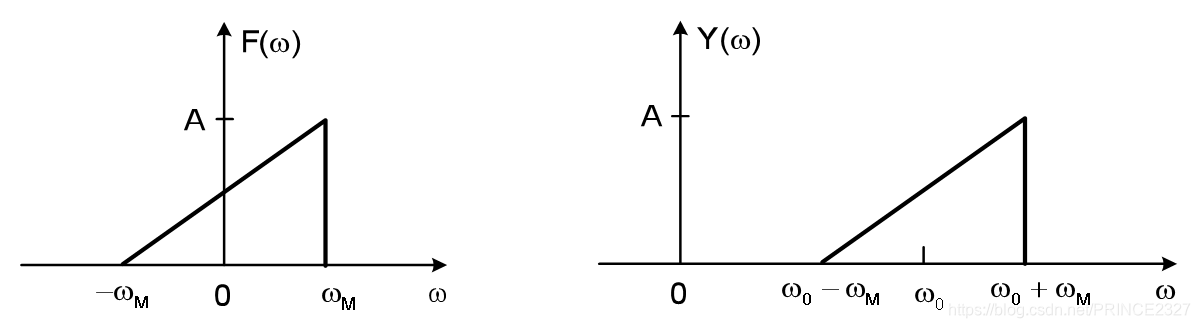
可以看出，这种调制方法事实上就是对输入信号的频谱进行搬移。

5.12 以复指数信号为载波信号的解调

基于上，可以很容易地看出，解调方法为：

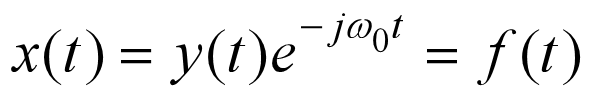
5.13 以正弦信号为载波信号的调制

以正弦信号为载波信号的幅度调制如下图：

同样有：



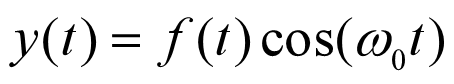
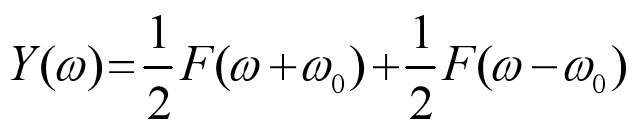
如上图， 可以看出，输入信号的形状决定了最终已调信号的形状。

5.14 以正弦信号为载波信号的解调

解调过程如下：


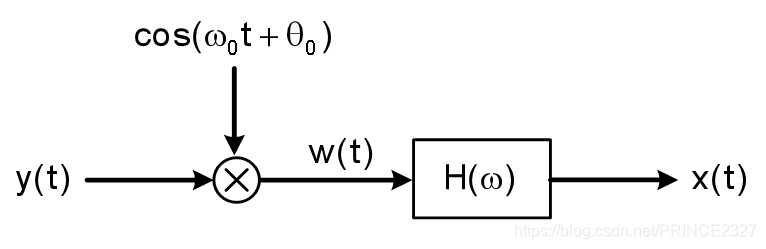
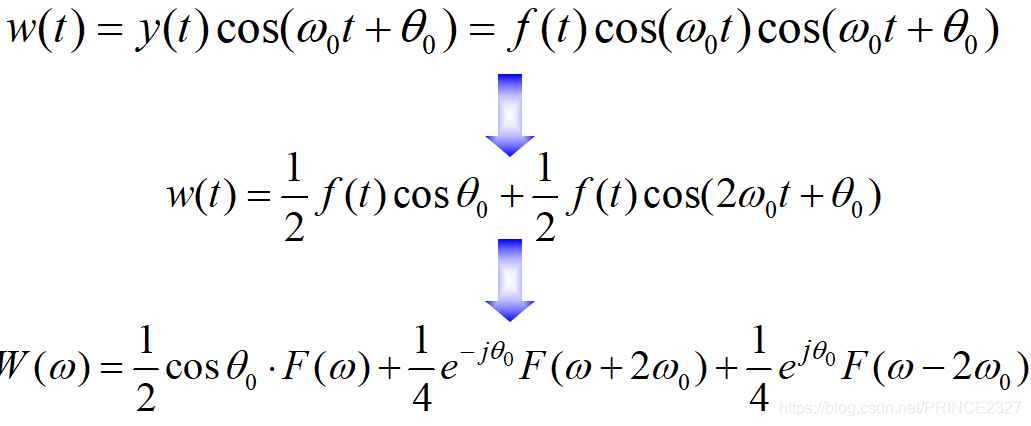
令 $H(w)$ 为：

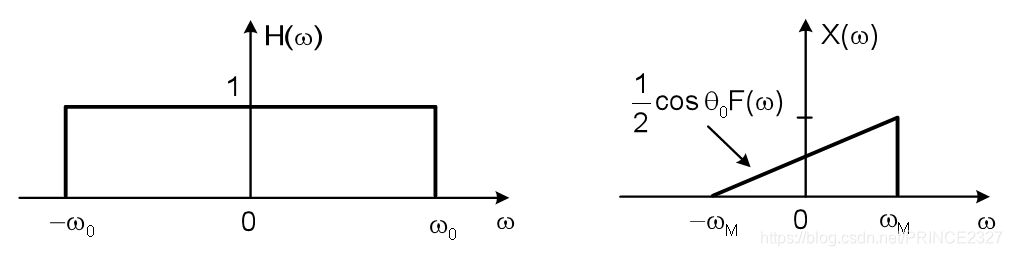
则有：


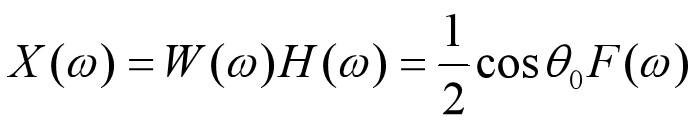
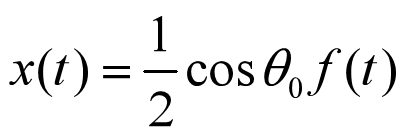
可以看出，并没有完全恢复输入信号。这里当 $\theta=0$时，所恢复出的信号强度最大（或者说最接近原信号）。据此我们就可以得到一个一般性的结论：当接收端的载波信号的初相位与发送端的载波信号的初相位相同时，恢复出来的效果最佳，此时的解调被称为同步解调。

5.15 本章小结

看似内容多，事实上只是FT性质的具体应用。本章重点可以如下概括：

1.引入一些新的概念，如无失真传输，系统相位，群延时等。

2.了解基本的采样方法及信号处理过程。

3.了解基本的通信过程及信号的传递

未经允许请勿转载

欢迎交流