题目
一群猴子要选新猴王。新猴王的选择方法是:让N只候选猴子围成一圈,从某位置起顺序编号为1~N号。从第1号开始报数,每轮从1报到M,凡报到M的猴子即退出圈子,接着又从紧邻的下一只猴子开始同样的报数。如此不断循环,最后剩下的一只猴子就选为猴王。请问是原来第几号猴子当选猴王?
输入格式:
输入在一行中给两个正整数N, M(1<= N,M ≤10000000)。
输出格式:
在一行中输出当选猴王的编号。
普通解法(暴力)
#include<stdio.h>
int main()
{
int n,m;
scanf("%d%d",&n,&m);
int num[1000];
for (int i = 0; i < n; i++)
num[i] = i + 1;
int i = 0,t = 0,count = 0;
while (1) {
if (num[i] != 0) {
if (count == n - 1)
break;
t++;
if (t == m) {
num[i] = 0;
t = 0;
count++;
}
}
i++;
if (i == n)
i = 0;
}
printf("%d",s+1);
return 0;
}
此方法很简单,在此不做详细阐述。
递归的思想求解(公式法)
#include<stdio.h>
int main()
{
int n, m, s = 0;
scanf("%d%d",&n,&m);
for (int i = 2; i <= n; i++) {
s = (s + m) % i;
}
printf("%d",s+1);
return 0;
}
这个程序看起来很难理解,现在我就解释以下如何来的:
首先我们定义一个函数f(N,M),用来表示,一共有N个猴子报数,每报到M淘汰掉那个猴子,最终函数值是最终胜利者的编号。
那么同理不难理解,f(N−1,M)表示,一共有N-1个猴子报数,每报到M时淘汰掉那个猴子,最终函数值是胜利者的编号。
那么递推公式就可以这样表示:f(N,M)=(f(N−1,M)+M)%N
下面我来解释以下如何得到这个公式:
首先为了方便,我们简化以下题目,一共有11个猴子,从第1号开始报数,每轮从1报到3,凡报到3的猴子即淘汰。
下面我们用数字从0开始表示每一个猴子:
0、1、2、3、4、5、6、7、8、9、10
首先我来告诉你,最后是6号猴子当了猴王,用函数表示即为f(11,3)=6,这样方便我们下面的讨论。
首先在刚开始时,头一个猴子编号为0,从它开始报数,第一轮被淘汰的是编号2的猴子。
淘汰后还剩下10个猴子,它们的编号依次为:
0、1、3、4、5、6、7、8、9、10
那么请注意,这时我们就可以这样理解:把第二轮报数的猴子当做队首,即就可以当做f(10,3)
我们画一张图来表示:(箭头为第二轮该第一个报数的猴子)
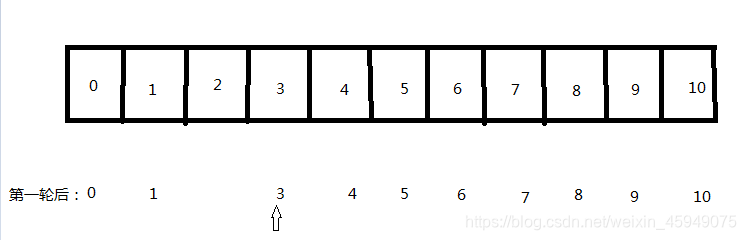
由于原来获胜者的编号为6,去掉了2号,也就是进行了一轮后,获胜者的绝对位置一定不变,也就是如下图:
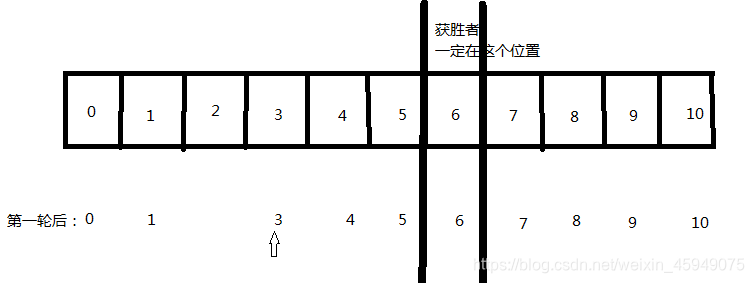
那么我们把3号当做第一个报数的猴子,也就是f(10,3),就会变成如下图所示:
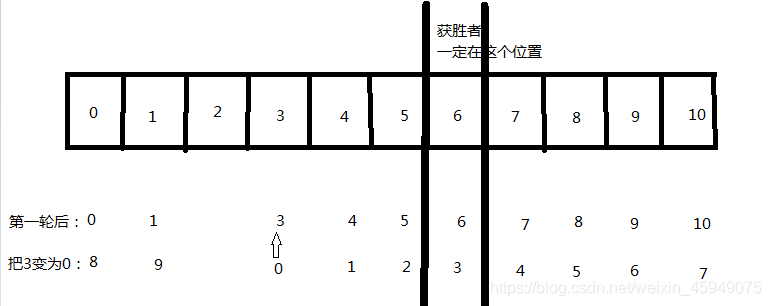
那么就可以很清楚地看出来,因为我们知道了11个猴子时获胜者为6号,那么10个猴子时获胜者就为3号,二者相差3,也就是相差了一个M的值。
看起来很巧合,但其实这并不是巧合,而是必然,因为不难理解,每一轮都是往后移动M=3个猴子,第一轮移了3只猴子后,把第二轮的首变为0,那么后面的所有猴子对应的编号都应该减3,即减去M。
那么我们就可以得到这样一个算式:f(10,3)=f(11,3) – 3
我们就可以得到:f(11,3)=f(10,3)+3
由于f(10,3)表示猴子的编号为0-9,f(11,3)表示猴子的编号为0-10,那么假如f(10,3)=9,那么f(10,3)+3=12,此时已经超过了f(11,3)的猴子的最大编号,所以我们需要用取余的方式来规避这种错误,即:f(11,3)=(f(10,3)+3)%11
因为猴子是围成圆圈来报数的,所以这样写也完全符合题意。
那么我们就得到了一个最终的结论,即f(11,3)=(f(10,3)+3)%11。
我们就可以用递归的思想:如果我们想求f(11,3)的值,那么我们只要知道f(10,3)的值就行;如果我们想求f(10,3)的值,那么我们只要知道f(9,3)的值就行;如果我们想求f(9,3)的值,那么我们只要知道f(8,3)的值就行 … … 如果我们想求f(2,3)的值,那么我们只要知道f(1,3)的值就行。
那么显而易见,我们就证明了上面的递推公式的正确:f(N,M)=(f(N−1,M)+M)%N
由题意,我们很容易可以知道,当只有一个猴子时,那么那只猴子自然就是猴王,也就是f(1,3)=0是一定的,由此我们就知道了这个递归的终止条件为f(1,3)=0。
所以让我们回到简化后的题目:求f(11,3)的值。
我们可以定义一个s和i的变量,s表示每个f(N,M)的值,i表示每次N的值,M的值是固定的3,那么当i=1时,即只有一个猴子,那么f(1,3)=0,即s=0(也就是把s初始化为0)。
然后i++后i=2,那么f(2,3)=(f(1,3)+3)%2=1;
然后i++后i=3,那么f(3,3)=(f(2,3)+3)%3=1;
然后i++后i=4,那么f(4,3)=(f(3,3)+3)%4=0;
… …
直到i=11时,那么f(11,3)=(f(10,3)+3)%11=6;
此时循环终止,也就是for中应该写的循环终止条件为i<=11,
那么简化后的题目的代码应该这样:
#include<stdio.h>
int main()
{
int s = 0;
for (int i = 2; i <= 11; i++) {
s = (s + 3) % i;
}
printf("%d",s+1);
return 0;
}
最后的s+1是由于我们一直把第一个猴子标号为0,但实际上题目要求是第一个猴子标号为1,所以最后需要再加1。
那么再回到原题,是让我们求f(N,M)的值,很容易通过类比得出最终的代码:
#include<stdio.h>
int main()
{
int n, m, s = 0;
scanf("%d%d",&n,&m);
for (int i = 2; i <= n; i++) {
s = (s + m) % i;
}
printf("%d",s+1);
return 0;
}
当然,这是把递归用for循环来写了,我们也可以把代码写成递归的形式:
#include<stdio.h>
int fun(int n,int m)
{
if(n==1)
return 0;
else
return (fun(n-1,m)+m)%n;
}
int main()
{
int n, m, s = 0;
scanf("%d%d",&n,&m);
s=fun(n,m);
printf("%d",s+1);
return 0;
}
注: 但是并不提倡大家用递归来写,因为数据太大,递归会占用太多的资源,在某些平台上编译会出现段错误。
