如果说吃一个包子不饱,两个包子不饱,到第五个才能饱。这是量变引起的质变。
如果说一个原始文明到一个古代文明再到一个近代文明到现代再到未来。这就是文明的传承。这两个都是前面的铺垫给了现在的辉煌
文明从来都没有灭亡。我们看不到不代表不存在,不仅存在还有可能是我们今朝的缩影。我们不是替换了它,而是一步步传承下去,想了好的方向发展。我们祖宗一辈辈的摸索到了现在中国乃至世界的辉煌。星火相传,奋飞不辍!
这一篇可能用到了一些数学知识,为了去写这一篇,我也是研究了很长时间了。本篇主要介绍平面点对问题,凸包问题,以及分治算法另一个改进途径:增加预处理
1、平面点对问题
什么是平面点对问题
我们先看一个例子:
输入:平面点集P中有n个点,n>1
输出:P中的两个点,其距离最小
对于这个问题我们首先可以用蛮力法进行解决。
蛮力法
所谓的蛮力法就是穷举的思路。在n个点中任取两个点计算距离,然后找到最小的距离,这就是问题的解
我们分析下不难发现,我们任取两个点进行计算距离,不就是C(n,2)的遍历过程,计算出来就是n(n-1)/2
或者说第一个点和剩下的n-1计算距离,比较;然后第二个点再和剩下的n-2个点(因为它和第一个点比较过了)计算距离,比较。这样下去也是n(n-1)/2
然而比较是O(1)的量,因此我们得出这个算法的时间复杂度就是O(n^2)。
大家还记得两点之间的距离公式吗,在P1(x1,y1),P2(x2,y2)。
我们有d=
这就是两点之间的距离公式。
下面我们来分析下代码:
代码写法很简单,首先我们可以根据点的个数进行分类讨论,如果是1个那就直接返回无穷大,如果是两个那就直接进行计算直接输出就行。2个以上的我们可以通过两个for循环进行处理。
从n个点中寻找另外的点。另外的点为了避免重复比较(就是第一个点和第二个点比较完,第二个又和第一个点进行了比较)那么我们可以让j=i+1,j<n。因此我们得出了i=0,i<n-1。也就是在比较第n-1个点到第n个点的时候就比较完了。对于计算和比较我们可以在内层循环进行。最后输出最短距离就行了。因此我们编写代码:
public static void main(String[] args) {
// TODO Auto-generated method stub
Point p[]= {new Point(2, 2),new Point(2, 4),new Point(2, 8),new Point(2, 10),new Point(2, -4),new Point(2, 18),new Point(6, 2)};
double mindes=Bruteforce(p, p.length);
System.out.println("最短距离是:"+mindes);
}
//计算两点直接的距离
public static double Des(Point p1,Point p2) {
return Math.sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y));
}
//蛮力法
public static double Bruteforce(Point p[],int length) {
if(length==1)
return 1e20;
else if(length==2)
return Des(p[0], p[1]);
else {
double mindis,temp;
mindis=Des(p[0], p[1]);
for(int i=0;i<length-1;i++)
for(int j=i+1;j<length;j++) {
temp=Des(p[i], p[j]);
if(temp<mindis)
mindis=temp;
}
return mindis;
}
}
public class Point {
double x;
double y;
public Point(double x, double y) {
super();
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
}
下面我们看一看分治法是怎么解决的。
分治法
分治法的思路就是:
1、将P在中间划分成左右平面,每个平面大概有n/2个点。
2、在左平面PL中找到一个最短的距离
3、在右平面PR中找到一个最短的距离
4、然后我们在这两个平面中找到最短的距离
5、然后我们分析中间那一块,找到跨平面的点的最短距离。
6、最后分析,找到4和5步的最短距离。这个最短距离就是问题的解
好,我们现在一步步的去进行分析
首先我们先以x坐标升序进行排序,如果x坐标相等,那么就要以y坐标进行升序排序。将点集合进行排列。这样我们通过划分,划分出的点总是彼此之间靠的最近。当然也是彼此之间距离最短的点。
对于前四步,我们可以通过递归的方式逐步划成两个点,以第n/2个的点(或者以第n/2和n/2 +1个点的中垂线)进行划分,左面两个点,右面两个点,中间是那个第n/2个点。然后调用点与点的距离公式计算,然后我们去进行判断,找到此时的左右平面中最短的距离
下面我们画个图介绍一下


好,接下来我们进行最后两步
对于最后两步跨平面进行分析,着实很难,但是也有法可解
这里我们介绍一种方法:

我们知道点P1向右不超过d,向上和向下也不超过d,故与点P1构成最短距离的点必然在这么一个d*2d的矩形框内

至于为什么不超过d?
大家想啊,如果p1p2之间的横坐标或纵坐标超过d。那么去想他们之间的距离是不是超过d了。这么说吧,如果两个点的横坐标整好差一个d,再不考虑纵坐标的情况下,两个点代入距离公式就是个d,那要是大于d呢,可不就是距离也大于d了啊
我们分析一下抽出来的模型
我们将矩形划成6个等大小的方格,如下图

我们得出斜线是5/6d,不超过d。那么一个方格只能存放一个点,这是因为两个点都在一个方格里面,那么它们之间的距离就会小于d。这可是与当初的以dmin为界划范围违背啊。
什么意思呢
就是说啊,当初在中间这里划一个dmin的范围,dmin怎么求得?不就是左右平面的最小距离吗,不懂的可以再回去看前四步。而你现在右面一个方格中两个点的距离小于d,这不就坑人了。所以一个方格内只能存放一个点。
那么也就是说左边的那个点P1啊,与右平面构成最短距离顶多就是6个点。当然右平面与左边也是6个点(实际上考虑左边就已经将右边考虑过了)。
那么具体是怎么做呢
首先将跨边界的点进行排序,假定第一个点是左边的点,看第二点,如果第二个点是左边的点就不考虑这个点,直到遇到右面的点,然后就检查第一个点和右面的点的距离是不是小于d。最后检查窄缝如上边的P2与其他点的距离。
我们分析出,跨边界在方格里面的点顶多考虑不超过12个点是O(1)的量,而在窄缝里的点顶多是计算n次(窄缝的点与其他在这个窄缝的点的左右以d范围的点的距离)所以是O(n)的量。
最后分析得出跨边界考虑的时间是O(n)
我们可以把跨边界的换一种思路来去编写代码

我们直接这样设d=min(d1,d2)假定中位线横坐标为X,那么范围就是[X-d,X+d]。也就是将左平面到右平面(包括自己)在那个范围的所有的点都存在一个集合或者数组里;然后我们将这里面的点的集合按照y坐标进行升序排序;然后将点集里面的点两两比较纵坐标的差值,将差值大于等于d的直接跳过,否则计算距离。这样得到的最小的距离与前面得到的dmin进行比较。最终得到真正的解。
我们对这个做法分析下,首先找点集就是O(n)的量,我们先不考虑排序。而对于最后的计算比较,虽然是两层循环,但是中间是有一个continue,是可以打断的。遇到差值大于等于d的直接跳过,对于这个就是比较,也就是O(1)的量。而小于d的才是真正进入循环计算的。当然也就是O(n)的量。所以最后不考虑排序的话就是O(n)的量。
这就是最后两步的做法
我们先上个伪码:

这里我们看到,第一步直接计算,或者说就是递归边界处理是O(1)的量
第二步是排序,时间复杂度是O(nlogn)(至于为什么是nlogn,大家可以搜搜排序的决策树就明白了)
第三部是计算然后进行划分也是O(1)
第4,5步对于递归就是2T(n/2)
第6步算左右平面最小距离也是O(1)
对于第7步,如果我们考虑排序的话不就是O(n)+O(nlogn)=O(nlogn)
最后我们分析出这个时间复杂度就是
T(n)=2T(n/2)+2O(nlogn)=2T(n/2)+O(nlogn)
T(n)=O(1),n<=3
这个我们可以通过递归树得

根据完全二叉树定理,n=2^k,即k=logn(n是节点数,k是深度)
将上图右边的式子相加得,
nlogn+n(logn-1)+n(logn-2)+…+n(logn-k+1)
= nlogn+nlogn+nlogn+…+nlogn-n(1+2+3+4+…+k-1)
= nklogn(有多少深度,就有多少的logn。绝对不是n个logn) -n(k(k-1)/2)
= nklogn-n((k2-k)/2
这里我们把k=logn带进去得,
= n(logn)2-n((logn)2/2-(logn)/2)
= n(logn)2-n(logn)2/2-n(logn)/2
= O(n(logn)2) (读作:logn的平方乘以n)
因此我们分析出时间复杂度就是:O(n(logn)2)=O(nlogn·nlogn)
那么有没有可以再改进的算法呢?
改进分治算法的途径
我们可以增加预处理的方式,降低上面问题的时间复杂度
在T(n)=aT(n/b)+f(n)中
增加预处理,从而减少f(n)
我们可以根据增加预处理来降低上面算法的时间复杂度
在递归前,对坐标进行排序,作为预处理
比如说:
我们可以把一开始对横坐标的排序放到递归方法的外面
把对纵坐标的排序直接删掉(增加对纵坐标的排序,是因为在计算两个点纵坐标的差值的时候是准确的进行大的减小的,也就是不会出现负值的情况),用绝对值(Math.abs())进行替代这一步操作。
当然我看网上有直接在递归方法里面用归并排序直接排,具体的可以参考网上的。这里不再深究了。
通过这样分析得出:
设,递归过程是W(n),预处理过程是O(nlogn)
T(n)=W(n)+O(nlogn)
W(n)=2W(n/2)+O(n)
W(n)=O(1),n<=3
我们通过主定理的方式得出W(n)=O(nlogn),因此T(n)=2O(nlogn)
故时间复杂度就变成了O(nlogn)
我们看到,通过增加预处理,已经把时间复杂度降到了O(nlogn)
具体代码分析
这里我们只重点分析下,跨边界代码
首先我们先创建集合
因为要将左平面到右平面(包括自己)在那个范围的所有的点都存在一个集合或者数组里
i=left,i<=right
if(Math.abs(p[mid].x-p[i].x)<=mindes)
然后将i加进集合里
最后我们要对点集寻求最短距离
那么循环范围是
i=0,i<List.size()-1
j=i+1,j<List.size()
然后我们拿出来存在该下标的值,p[值]就是.y就是这个点的纵坐标(有点绕,这个问题多想想)
if(Math.abs(p[pointy.get(i)].y-p[pointy.get(j)].y)>=mindes)
continue;
如果小于mindes(最短距离),那么我们就计算两点之间的距离。两点之间的距离还小于mindes,那么这个最小距离就是我们要的解了
接下来,上代码
public static void main(String[] args) {
// TODO Auto-generated method stub
Point p[]= {new Point(2, 2),new Point(2, 4),new Point(2, 8),new Point(2, 10),new Point(2, -4),new Point(2, 18),new Point(6, 2)};
Arrays.sort(p, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
// TODO Auto-generated method stub
if(o1.x>=o2.x) {
if(o1.x>o2.x)
return (int) (o1.x-o2.x);
else
return (int) (o1.y-o2.y);
}
else return (int) (o1.x-o2.x);
}
});
double mindes2=Dividepoint(0, p.length-1, p);
System.out.println("最短距离是:"+mindes2);
}
//计算两点直接的距离
public static double Des(Point p1,Point p2) {
return Math.sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y));
}
//分治法
public static double Dividepoint(int left,int right,Point p[]) {
double mindes=1e20;
if(left==right)
return mindes;
else if(left+1==right)
return Des(p[left], p[right]);
else {
int mid=(left+right)>>1;
double LeftminDes=Dividepoint(left, mid-1, p);
double RightminDes=Dividepoint(mid+1, right, p);
if(LeftminDes>=RightminDes)
mindes=RightminDes;
else
mindes=LeftminDes;
List<Integer> pointy=new ArrayList<Integer>();
for(int i=left;i<=right;i++)
{
if(Math.abs(p[mid].x-p[i].x)<=mindes)
pointy.add(i);
}
for(int i=0;i<pointy.size()-1;i++)
for(int j=i+1;j<pointy.size();j++) {
if(Math.abs(p[pointy.get(i)].y-p[pointy.get(j)].y)>=mindes)
continue;
double temp=Des(p[pointy.get(i)],p[pointy.get(j)]);
if(temp<mindes)
mindes=temp;
}
return mindes;
}
}
public class Point {
double x;
double y;
public Point(double x, double y) {
super();
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
}
对于这个代码你也许会问,在处理跨边界问题的时候,两个同一面的点会不会进行比较?
大家看啊,我们划分的只有两个点,所以说一边平面的点我们已经计算完了,而且也已经和另一面的比较完了。所以同一面的另外一个点是不会加进集合里面的。大家看啊,我们划分的只有两个点,所以说一边平面的点我们已经计算完了,而且也已经和另一面的比较完了。所以同一面的另外一个点是不会加进集合里面的。
我们已经知道了,改进分治算法的途径有两种:1、减少子问题的个数(a),2、增加预处理(fn)
2、凸包问题
什么是凸包问题?
百度上给的答案:在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1,…Xn)的凸组合来构造.
也就是:
给定大量离散点集合Q,求一个最小的凸多边形,使得Q中的点在该多边形内或者边上
说白了就是找一个大的凸多边形,可以包含所有的点
例如:
找到一个大的凸多边形,可以包含所有的点
这个问题的解:

凸包问题应用非常广泛:可以用于字形识别、碰撞检测。我觉得仅一个碰撞检测就能涉及到不少行业
凸包问题的算法
蛮力法
对于一个n个点集合中的两个点p1和p2,当且仅当该集合中的其它点都位于穿过这两点的直线的同一边时,它们的连线就是该集合凸包边界的一部分,简言之,p1和p2就是凸包问题中最小凸多边形的顶点。对每一对点都做一遍检验之后,满足条件的线段就构成了该凸包的边界。
就是说任取两个点连接成一条直线,考虑剩下的几个点是否全部都在所连接的直线的同一侧。如果是,则将这个点加进数组或集合里;若存在一个点不在同一侧,则这个点将被抛弃,最后输出数组或集合里面的点就是问题的解
那么首先考虑一个问题,如何判断一个点在直线的哪一侧。
根据过两点的直线方程,得:

(具体的计算过程我忘了,大家可以上网搜搜)
我们只需要把测试的点,即P3代进去就可以知道符号(正负),若得到的结果为正值,则点在直线的左侧;若得到的结果是负值,则点在直线的右侧;若得到结果为0,则点在线上我们只需要把测试的点,即P3代进去就可以知道符号(正负),若得到的结果为正值,则点在直线的左侧;若得到的结果是负值,则点在直线的右侧;若得到结果为0,则点在线上
然后要的点一般都是>=0或者<=0。如果在判断的过程中出现了异号的情况,那么就不是要的点,舍弃掉,寻找下一个点。
这里就不再分析了,直接上代码
public static void main(String[] args) {
// TODO Auto-generated method stub
Point p[]= new Point[8];
p[0] = new Point(1,0);
p[1] = new Point(0,1);
p[2] = new Point(0,-1);
p[3] = new Point(-1,0);
p[4] = new Point(2,0);
p[5] = new Point(0,2);
p[6] = new Point(0,-2);
p[7] = new Point(-2,0);
Point[] result = getconvexhull(p);
System.out.println("集合中满足凸包的点集为:");
for(int i = 0;i < result.length;i++)
System.out.println("("+result[i].x+","+result[i].y+")");
}
//蛮力法
public static Point[] getconvexhull(Point p[]) {
Point result[]=new Point[p.length]; //存放凸包点集
int lr=0;
int flag=0;
int len=0; //记录凸包点集的个数
int k;
for(int i=0;i<p.length;i++)
for(int j=0;j<p.length;j++) {
if(i==j)
continue;
for(k=0;k<p.length;k++) {
double a=p[j].y-p[i].y;
double b=p[i].x-p[j].x;
double c=p[i].x*p[j].y-p[i].y*p[j].x;
double value=a*(p[k].x)+b*(p[k].y)-c;
if(value>0) {
if(flag==0)
flag=1;
lr=1;
}
else if(value<0) {
if(flag==0)
flag=-1;
lr=-1;
}
if(lr!=flag)
break;
}
flag=0;
lr=0;
if(k==p.length) {
result[len++]=p[i];
break;
}
}
Point[] result1 = new Point[len];
for(int m = 0;m < len;m++)
result1[m] = result[m];
return result1;
}
public class Point {
double x;
double y;
public Point(double x, double y) {
super();
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
}
蛮力法分析
我们看到任取两个点就是n(n-1)/2,而再和剩余的n-2个点进行比较(比较:O(1))。因此
T(n)=(n-2)·(n(n-1)/2)
因此蛮力法的时间复杂度就是O(n^3)
分治法
我们先介绍两个概念:上包和下包
任意连接平面的两个点所构成的直线,直线的上(左)方所构成的平面是上包,直线的下(右)方所构成的平面是下包。
我们再上包或者下包中找到一个Pmax,使Pmax离直线的距离最大。任取的两个点分别与Pmax点相连,进行划分
而对于一开始的任取两点,先将点集排序,我们一般是取横坐标最小的点(如果横坐标最小的点有多个则选取纵坐标最小的点)和横坐标最大的点(如果横坐标最大的点有多个则选取纵坐标最大的点),选取的两个点上面是上包,下面是下包。随后再上(下)包中找到距直线最大距离的点Pmax。
大家想一想任取的那两个点是一定在凸包上的。
然后任取的两个点分别与点Pmax相连。所围成的是一个三角形平面。举例如下:
例如这些点

首先我们先找到横坐标最小和最大的点,然后连接起来

然后在上包(即直线上边的平面)寻找一个距直线最大距离的点Pmax,然后分别与P1,P2相连

那么我们发现在上包中,用三角形划分了几个区域,P1Pmax左边的会产生下一个上包的Pmax,P2Pmax的右边也会产生下一个下包的Pmax。三角形区域里面的是包含的点
我们再解决几个问题:
1、怎么判断直线的上下包以及寻找Pmax
2、怎么进行递归划分以及下一个要寻找的上下包以及Pmax
3、返回的解是什么,怎么处理
我们先看第一个问题。如何寻找直线同一侧的点的问题,我们再上边已经介绍过了一种方法。这里我们再说一种最常规的方式
我们将上图的P1P2为一有向直线,定P1指向P2。如图

然后我们用矩阵来判断点在直线的左方还是右方:
P1P2是一有向直线,P1(x1,y1),P2(x2,y2)。现有一P3(x3,y3),判断P3在直线的哪一侧
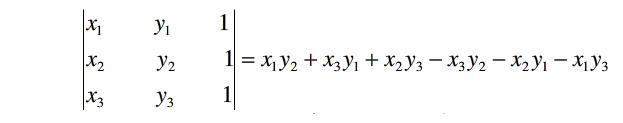
结果大于0,则P3在直线的左侧;结果小于0,则P3在直线的右侧;结果等于0,点在线上
而寻找最大距离Pmax,就是我们可以用点到直线的距离公式:

下面我们解决第二个问题
递归划分,我们可以通过P2在P1Pmax的左侧还是右侧来进行划分
若是左边则P2Pmax是下一个小凸包里的上包,P1Pmax则是下一个小凸包里的下包
否则就是P2Pmax是下一个小凸包里的下包,P1Pmax则是下一个小凸包里的上包
这里我们考虑一个临界问题:

假设这是上包的边,上边已经没有点了。所以P1P2肯定是凸包上的两个点,但是有一个点Pmax与P1P2共线,如果题目让你找出凸包上的所有点,那么点Pmax这个点是不能舍弃的,看图能看出来P1Pmax这个边是要归在上包里面的,而P2Pmax是要归到下包里面的。因为有向直线P1Pmax的左边没有点了,而有向直线P2Pmax的右边也没有点了。

同理P1Pmax是要归在下一个小凸包的下包里的,P2Pmax是要归到上包里的。
也就是说在研究上(下)包时,如果碰到三点不共线的时候,判断P2在哪一侧。然后划分出下一个上下包的点递归求解,直到再也找不到Pmax,就说明某一侧再也没有点了;如果碰到三点共线的时候。就可以按照上边的进行考虑;如果遇到了没有找到Pmax,我们就可以把P1加到点集中(如果上包将P1加到点集,下包就加P2;反之也可以),最后我们直接返回点集,就解决了第四个问题了。最后那个点集里面所有的点就是问题的解。
直接上代码:
public static Point ch[];
public static int num=0;
public static void main(String[] args) {
// TODO Auto-generated method stub
Point p[]= new Point[8];
p[0] = new Point(2,0);
p[1] = new Point(0,2);
p[2] = new Point(0,-2);
p[3] = new Point(-2,0);
p[4] = new Point(1,0);
p[5] = new Point(0,1);
p[6] = new Point(0,-1);
p[7] = new Point(-1,0);
//将x坐标按升序排序,若x相同则按照y排序
Arrays.sort(p, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
// TODO Auto-generated method stub
if(o1.x>=o2.x) {
if(o1.x>o2.x)
return (int) (o1.x-o2.x);
else
return (int) (o1.y-o2.y);
}
else return (int) (o1.x-o2.x);
}
});
ch=new Point[p.length];
dchull(0, p.length-1, p);
uchull(0, p.length-1, p);
Point[] result = new Point[num];
for(int i = 0;i < num;i++)
result[i] = ch[i];
System.out.println("集合中满足凸包的点集为:");
for(int i = 0;i < result.length;i++)
System.out.println("("+result[i].x+","+result[i].y+")");
}
//三个点的叉乘
public static double mul(Point p1,Point p2,Point p3) {
return p1.x*p2.y+p3.x*p1.y+p2.x*p3.y-p3.x*p2.y-p2.x*p1.y-p1.x*p3.y;
}
//点到直线的距离
public static double distance(Point p1,Point p2,Point p3) {
return Math.abs((p2.y-p1.y)*p3.x+(p1.x-p2.x)*p3.y+(p1.y-p2.y)*p1.x+(p2.x-p1.x)*p1.y)/Math.sqrt(Math.pow(p2.y-p1.y,2)+Math.pow(p1.x-p2.x,2));
}
//下包分治法求解
public static void dchull(int a,int b,Point p[]) {
int j=-1,l,r,dch,uch;
double dis=-1;
//判断传入的下标所表示的点在坐标系的位置,左边的下标赋给l,右边的赋给r
if(a<=b) {
l=a;
r=b;
}
else {
l=b;
r=a;
}
//根据叉乘来找到一个点在直线的右边,并且与p[a]和p[b]所连接直线的最大距离的pmax
for(int i=l+1;i<r;i++) {
if(mul(p[a], p[b], p[i])<=0) {
if(distance(p[a], p[b], p[i])>dis) {
dis=distance(p[a], p[b], p[i]);
j=i;
}
}
}
//未找到,则这两个点就是在凸包上直接相连的点
if(j==-1) {
ch[num++]=p[a];
return;
}
//判断p[b]是在p[a]和p[j]所连接直线的左边还是右边
//若是左边则p[b],p[j]是下一个小凸包里的上包,p[a],p[j]则是下一个小凸包里的下包
//否则就是p[b],p[j]是下一个小凸包里的下包,p[a],p[j]则是下一个小凸包里的上包
if(mul(p[a], p[j], p[b])<0) {
uch=a;
dch=b;
}
else {
uch=b;
dch=a;
}
dchull(dch, j, p);
uchull(uch, j, p);
}
//上包分治法求解
public static void uchull(int a,int b,Point p[]) {
int j=-1,l,r,dch,uch;
double dis=-1;
//判断传入的下标所表示的点在坐标系的位置,左边的下标赋给l,右边的赋给r
if(a<=b) {
l=a;
r=b;
}
else {
l=b;
r=a;
}
//根据叉乘来找到一个点在直线的右边,并且与p[a]和p[b]所连接直线的最大距离的pmax
for(int i=l+1;i<r;i++) {
if(mul(p[a], p[b], p[i])>=0) {
if(distance(p[a], p[b], p[i])>dis) {
dis=distance(p[a], p[b], p[i]);
j=i;
}
}
}
//未找到,则这两个点就是在凸包上直接相连的点
if(j==-1) {
ch[num++]=p[b];
return;
}
//判断p[b]是在p[a]和p[j]所连接直线的左边还是右边
//若是左边则p[b],p[j]是下一个小凸包里的上包,p[a],p[j]则是下一个小凸包里的下包
//否则就是p[b],p[j]是下一个小凸包里的下包,p[a],p[j]则是下一个小凸包里的上包
if(mul(p[a], p[j], p[b])<=0) {
uch=a;
dch=b;
}
else {
uch=b;
dch=a;
}
dchull(dch, j, p);
uchull(uch, j, p);
}
public class Point {
double x;
double y;
public Point(double x, double y) {
super();
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
}
最后我们分析一下。大家想一个最坏的情况。如果一边只有一个点。而另一边却是n-1个点的情况。我们按照这个情况进行分析:
总时间复杂度:T(n)
对点集进行排序(预处理):O(nlogn)
递归过程:W(n)
找Pmax:O(n)
根据点的位置进行划分:O(1)
递归调用:W(n-1)
则W(n)=W(n-1)+O(n)
我们通过递归树解出:W(n)=O(N^2)
则T(n)=O(n^2)+O(nlogn)
T(n)=O(n^2)
因此最坏时间复杂度就是O(n^2)
而平均时间复杂度就是可以参考快速排序得出:O(nlogn)
而对于Graham扫描法,我们下一篇再提
###### 察己则可以知人,察今则可以知古。《吕氏春秋·览·慎大览》
