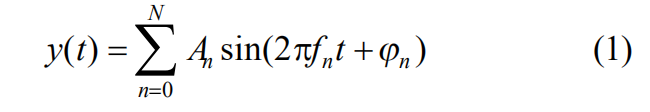前言
本文是对王小华的一篇论文《一种新的基于神经网络的高精度电力系统谐波分析算法》的理解和代码实现,涉及电气专业的一个课程设计,通过它可以对一个信号进行类似于傅里叶变换的频谱分析。它主要依靠单层神经网络来实现,将频谱信息放到单层神经网络权重中,然后用采集到的系列样本点去迭代优化这些权重参数,优化完成的权重参数通过简单的计算便可得到原信号的频谱,经过试验,精度非常高。
模型建立
任何一个周期函数都可以表示成一个基波与若干谐波的加权和,这是傅里叶变换的知识,表达式如式(1)所示。式中![]() 为初始相位,An为每个谐波分量的权值,N为基波与谐波的总数,fn为每个分量的频率值,f1为基波频率。
为初始相位,An为每个谐波分量的权值,N为基波与谐波的总数,fn为每个分量的频率值,f1为基波频率。
利用两角和的正弦公式展开式(1),可以得到式(2).式中A0为直流分量,如果此时知道y(t)的函数方程,我们可以通过公式很容易计算出权值![]() 和权值
和权值![]() 。但此处不用公式,而通过迭代优化的方式来估计这两类参数。
。但此处不用公式,而通过迭代优化的方式来估计这两类参数。
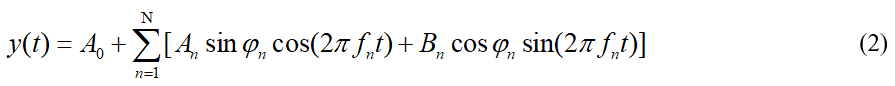
易知![]() ,再令
,再令![]() ,则式(2)可以化为式(3),式中为了化成单独的项的累加,第三项恒等变形到了N+1到2N的范围,细心点就会发现这个表达式像极了单层神经元模型,输入是2N+1个值组成的一个2N+1维列向量C,权重也是2N+1个值组成一个2N+1维的列向量W。
,则式(2)可以化为式(3),式中为了化成单独的项的累加,第三项恒等变形到了N+1到2N的范围,细心点就会发现这个表达式像极了单层神经元模型,输入是2N+1个值组成的一个2N+1维列向量C,权重也是2N+1个值组成一个2N+1维的列向量W。
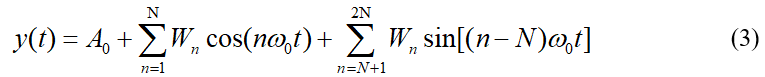
取![]() ,当n=1,2,....8,,N时。
,当n=1,2,....8,,N时。
取![]() ,当n = N+1,N+2...........2N。时
,当n = N+1,N+2...........2N。时
取![]()
则式(3)便可化为式(4)
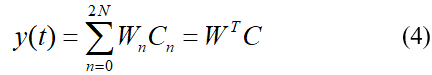
实际的过程中我们不可能知道每个时间点t时的函数值,我们只能知道我们所采样的时刻的采样值,假设采样间隔为Ts,第m次采样对应的时刻即为mTs。现在用mTs代替t改写(4),得到式(5),可知现在与y是m的函数,而m指第几次采样。
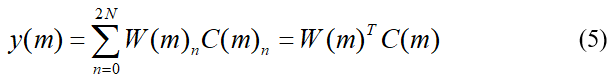
现在开始对原信号采样,每得到一个采样值,就进行一次迭代。此处借用论文作者的图来表示这个单层神经网络模型图,假设这是第m次采样,由第m次的时间t=mTs,可以算出其对应的C(m),然后将其与上一次迭代更新的权重W(m)相乘,便可得到此次的预测函数值![]() ,将预测结果,与对原函数第m次采样的采样值
,将预测结果,与对原函数第m次采样的采样值![]() 作差,便可得到预测误差
作差,便可得到预测误差![]() ,然后通过梯度下降更新参数W(m)得到W(m+1),完成一次迭代。
,然后通过梯度下降更新参数W(m)得到W(m+1),完成一次迭代。
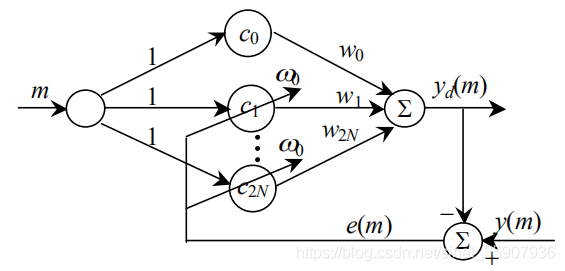
模型的损失函数由式(6)给出
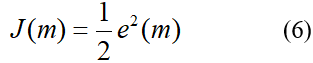
则梯度下降公式便可由式(7)给出

对于 ![]() 值,论文中通过大量计算证明其应该满足
值,论文中通过大量计算证明其应该满足![]() ,在实验中取的0.1,取得了较好效果。
,在实验中取的0.1,取得了较好效果。
另外,理论上,基波频率应该等于工频频率,即50Hz,但是由于各方面因素,可能不等,所以![]() 也是一个我们需要估计的量。
也是一个我们需要估计的量。
其梯度下降公式如式(8)
![]()
对于 ![]() 值,文中也只说明取上述范围,实验中取
值,文中也只说明取上述范围,实验中取![]() -1,取得了较好的效果。既快速,也没有产生振荡。
-1,取得了较好的效果。既快速,也没有产生振荡。
参数的提取
在迭代完成,获得合适的W与w0之后,可以通过如下公式提取出原信号各谐波的幅值和初始相位,当然还包括各谐波分量的w=n*w0。到这里就把一个在时域里的信号,转换成了多个谐波的叠加,即完成了频谱分析。
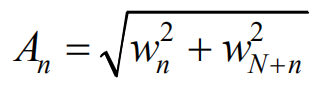
![]()
式中,wn即Wn,N为基波与谐波分量的个数。其中相位,由于arctan的值域只在【-0.5pi,0.5pi】之间,但是真实的角度是在【-pi,pi】之间的,所以需要根据wn与wN+n的正负关系来调整初始相位的值。
matlab代码实现
利用论文所测试用的信号进行测试,得到了比论文更好的效果。测试信号参数如下图所示。
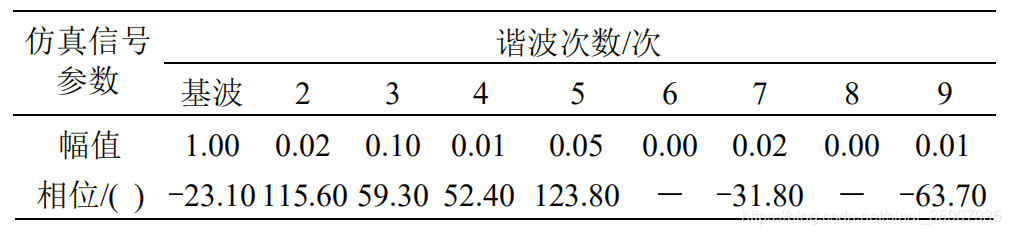
基波频率为50.2Hz,采样频率为1000Hz,m=80。
单独用80个点做一次大循环,在已知w0=50.2Hz的情况下,可以得到较好的结果,但是把w0初始值设置为工频50Hz之后,由于优化的难度加大了,而且学习率不能太高,要进行1000个这样的大循环才能做到和原始信号基本0误差的估计。另外,在本参数条件下,如果w0初始值小于48.3左右,那么最后分析出来的频谱与真实的频谱之间差距很大,但是用该估计的频谱可以基本拟合原信号,说明这是一个局部最优解,尝试了很多办法,无法跳出这个局部的误差极小值点。
clear all
An = [1.00,0.02,0.10,0.01,0.05,0.00,0.02,0.00,0.01]; %实际的基波与谐波的幅值
Bn = [-23.10,115.60,59.30,52.40,123.8,0.0,-31.80,0.0,-63.70]; %谐波幅值
F1 = 50.2;
Ts = 1/1000;
y = zeros(1,80);
W = 2*rand(1, 19) - 1; %随机 W
w = 2*pi*50;
Cn = zeros(1,19);
a = 0.1;
E2 = 0;
I = zeros(1,9);
Wa = zeros(1,9);
Wb = zeros(1,9);
P = zeros(1,9);
Q = zeros(1,9);
for q = 1:1000 %做epoch
y = zeros(1,80);
y1 = zeros(1,80);
y2 = zeros(1,80);
for k = 1:80
Cn(1) = 1;
for n = 1:9
y(k)=y(k)+An(1,n)*sin(2*pi*n*F1*k*Ts+Bn(1,n)*pi/180); %实际的信号值,在t = k*Ts时
Cn(n+1) = cos(n*w*k*Ts);
Cn(n+10) = sin(n*w*k*Ts);
I(n) = n;
Wa(n) = W(n+1);
Wb(n) = W(n+10);
P(n) = Cn(n+1);
Q(n) = Cn(n+10);
end
y1(k) = W*Cn'; %预测的信号值,在t = k*Ts时
E(k) = y(k)-y1(k);
w = w + 0.4*E(k)*k*Ts*sum(I'.*Wb'.*P'-I'.*Wa'.*Q');
W = W + 0.1*E(k)*Cn;
end
end
F2 = w/2/pi;
for i = 1:9
An1(i) = sqrt(W(i+1)*W(i+1)+W(i+10)*W(i+10));
if (W(i+10)>0)
Bn1(i) = atan(W(i+1)/W(i+10))*180/pi;
elseif (W(i+10)<0)&(W(i+1)>0)
Bn1(i) = atan(W(i+1)/W(i+10))*180/pi+180;
elseif (W(i+10)<0)&(W(i+1)<0)
Bn1(i) = atan(W(i+1)/W(i+10))*180/pi-180;
end
E2 = E2+(An(i)-An1(i))^2;
end
for k = 1:80
for n = 1:9
y2(k)=y2(k)+An1(1,n)*sin(2*pi*n*F1*k*Ts+Bn1(1,n)*pi/180); %实际的信号值,在t = k*Ts时
end
end
E2 = sqrt(E2)
figure(1);
plot(E.^2)
figure(2)
plot(y1)
hold on;
plot(y)结果
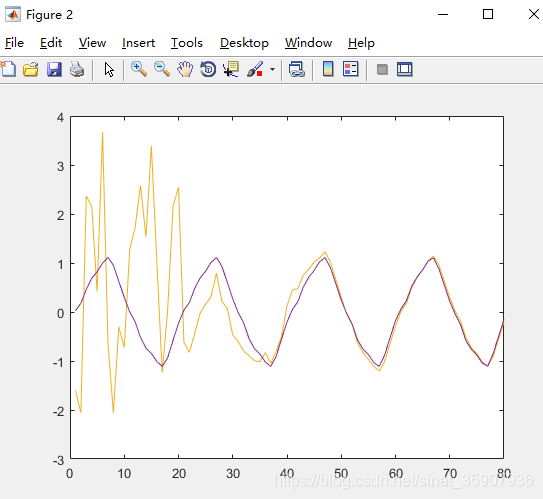
1.只进行一个大循环时误差与拟合情况。可以见到开始时基本预测错误,到30个点的训练之后,预测误差明显减少,也就是通过当前估计的频谱还原的函数与原函数的误差越来越小,梯度下降起了作用。

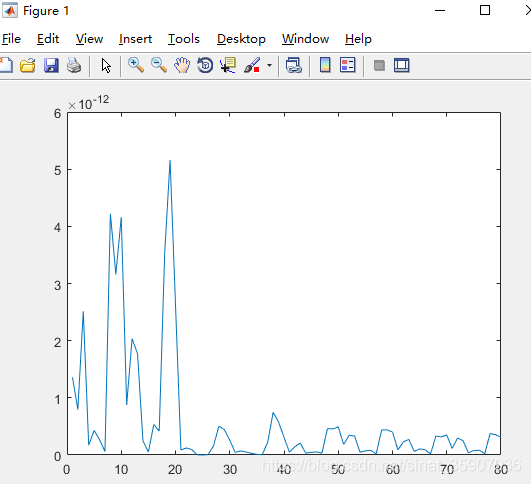
2.进行1000个大循环时的误差与拟合情况。到一千次时误差已经趋近于零,估计出来的频谱所还原的函数和原函数看起来几乎一模一样,完全拟合。
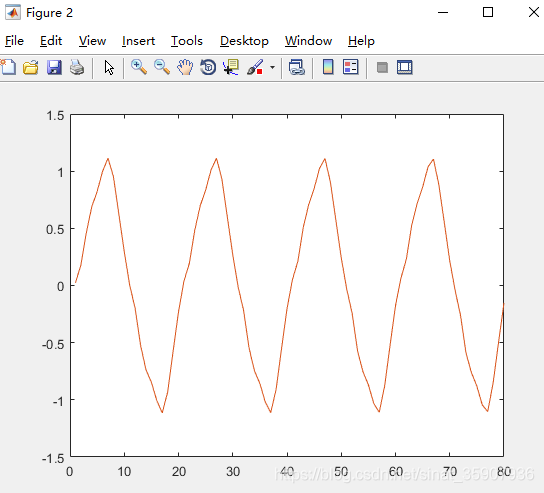
3.大循环1次时估计的频谱参数如下
信号的谐波幅值与各谐波的初始相位。


通过算法分析出来的谐波幅值与各谐波的初始相位。
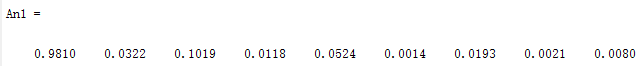


此时误差还很大。
4.大循环1000次时估计的频谱参数如下
信号真实的谐波赋值与各谐波的初始相位。


通过算法分析出来的谐波幅值与各谐波的初始相位。


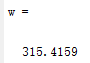
通过实验结果可以发现,用神经网络对一个信号做频谱分析,有限采样点,但是迭代次数足够高的情况下,误差可以控制在千分之一以下,是一种超级高精度的频谱分析手段。
参考:
王小华,何怡刚.一种新的基于神经网络的高精度电力系统谐波分析算法[J].电 网 技 术.2005.