@
概念
邻项交换排序是一种常见的贪心算法,它把决定相邻两个元素先后的决策推广到整个序列,从而获得最优解。
Ⅰ:P1080 国王游戏
题目链接
题目描述
恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 n 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
输入格式:
第一行包含一个整数 n,表示大臣的人数。
第二行包含两个整数 a 和 b,之间用一个空格隔开,分别表示国王左手和右手上的整数。
接下来 n 行,每行包含两个整数 a 和 b,之间用一个空格隔开,分别表示每个大臣左手和右手上的整数。
输出格式:
一个整数,表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
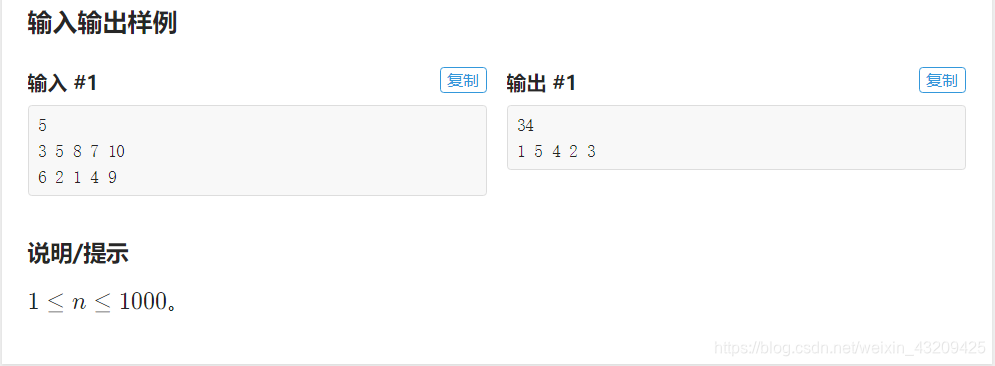
输入样例#1:
3
1 1
2 3
7 4
4 6
输出样例#1:
2
【数据范围】
对于 20%的数据,有 1≤ n≤ 10,0 < a,b < 81≤n≤10,0<a,b<8;
对于 40%的数据,有1≤ n≤20,0 < a,b < 81≤n≤20,0<a,b<8;
对于 60%的数据,有 1≤ n≤1001≤n≤100;
对于 60%的数据,保证答案不超过 10^9109;
对于 100%的数据,有 1 ≤ n ≤1,000,0 < a,b < 100001≤n≤1,000,0<a,b<10000。
思路
设 i 和 j 是相邻的两个大臣,设 两者 前面的所有大臣左手上的数的乘积为 k,则
①若 i 在 j 前面,则这两个大臣获得奖赏的较大值为
②若 i 在 j 后面,则这两个大臣获得奖赏的较大值为
因为题意要求最大值最小,我们设 i 在 j 前面更优,则此时需要满足
又有
则上式等价于
然后把这个式子(决策)推广到整个序列,即根据这个优先级排序,那么最后得到的解肯定是最优解了。
可能有人会疑惑,为什么可以 推广到整个序列? 万一 i 和 j 不相邻呢?
对于整个序列来说,需要序列所有的邻项满足上述决策,即等价于按照这个决策排序
不是很理解的话我们来模拟一下,上面我们已经证明任意两个相邻的元素需要满足上式才可以保证这两个元素的最优解,我们先按照上述决策排好序,那么对于任意两个不相邻的元素 i 和 j (假设 j 在 i 后面),互换两个位置的元素,则必然不再满足
同时不再满足的还有
和
对于(1)式: 第一行不等式的元素是相邻的,我们交换它们的元素,这样第一行就满足了,此时第二行的元素又是相邻的了,我们再交换... 直到最后原来 i 上的元素到了 j 位置上,而原来 i 到 j 的元素都往前移了一位,此时利用邻项交换排序完全满足了(1)式;
同理,对于(2)式: 最后一行不等式的元素是相邻的,我们交换它们的元素,然后倒数第二行的元素相邻,再交换...直到原来 j 上的元素到了i 位置上,此时利用邻项交换排序完全满足了(2)式。
由此: 整个序列没有哪个邻项顺序不满足我们的决策。
上述题目看起来已经可以说明邻项交换的精髓:推出决策 ,那么再来看一道
Ⅱ:P2123 皇后游戏
题目链接


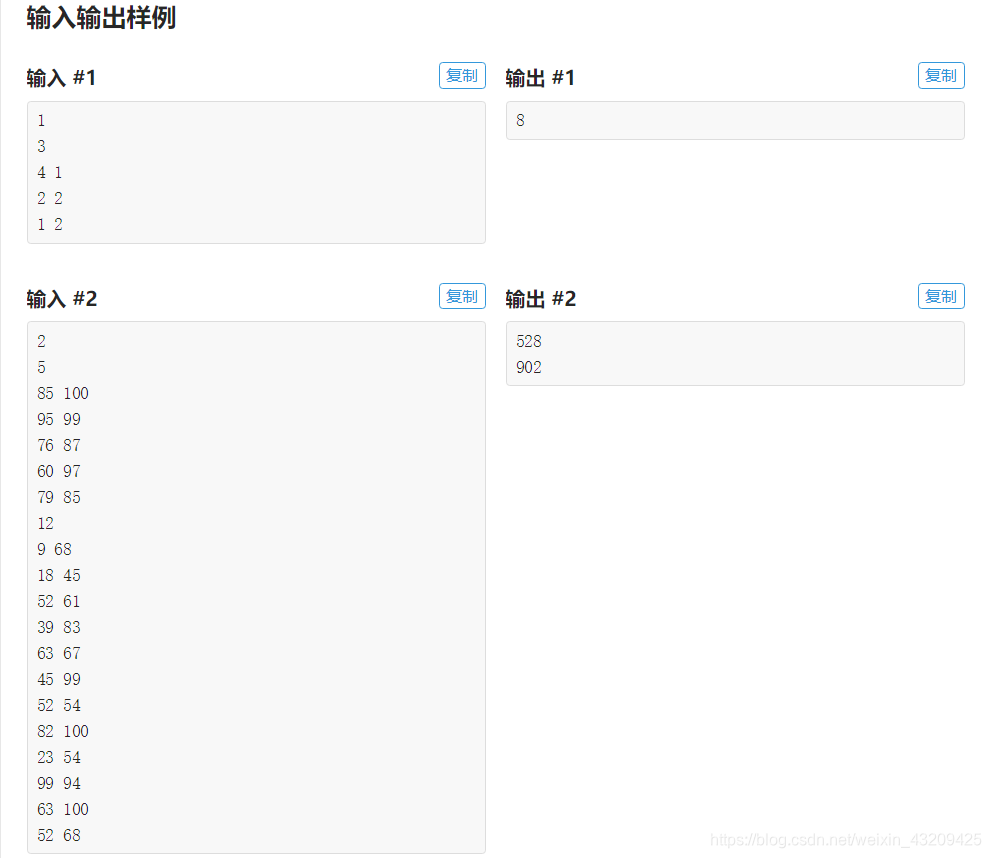

由题意,我们设大臣 i 和 j 相邻,两个大臣的前面一个大臣的奖金为 C,两个大臣前面所有大臣左手上的数之和为 sum,则
①若 i 在 j 前面,则这两个大臣获得奖金的较大值为 $$max(max(C,sum+a_{i})+b_{i},sum+a_{i}+a_{j})+b_{j},即$$
②若 i 在 j 后面,则这两个大臣获得奖赏的较大值为$$max(max(C,sum+a_{j})+b_{j},sum+a_{i}+a_{j})+b_{i},即$$
题意求最大值最小,我们设 i 在前面更优,则有
把里面的max拆开,即
其中左右两边均有
消去(后面解释为啥可以消去),然后变成了
消去 sum 得
化简,得
移项
观察左右两边都是较大的数被消去,留下较小的数的相反数,换一种写法即
消去负号
看样子,我们求出了最终最简决策,然后同样推广到整个序列,可以得到最优解。
为什么可以消去同项,我们可以把上面式子简化为
\[max(a1,b1,c) \leqslant max(a2,b2,c) \]那么若 c 是所有数中最大的,那么左右两边是相等的,不管换不换都一样
若 c 不是所有数中最大的,那就不用管 c 的存在了,因为决定这个不等式成立的只能是比 c 更大的元素。
所以,可以消去 c
但是,这个决策是不对的。不过与其说是不对,用 不完整 形容更好一些,
标准解释是因为这个决策不满足 严格弱序 中的 不可比性的传递性 。我们直接用一组数据说明
这就简单解释了何为 不可比性的传递性 ,即 \(a<=b,b<=c\) 无法推出 \(a<=c\),这种情况下就不能直接推广到整个序列了,需要做些补充来满足 不可比性的传递性 才行。
我们知道冲突的产生在于 \(min(b_{i},a_{j}) = min(b_{j},a_{i})\) 邻项要不要交换模糊不清,再分析题目给出的式子
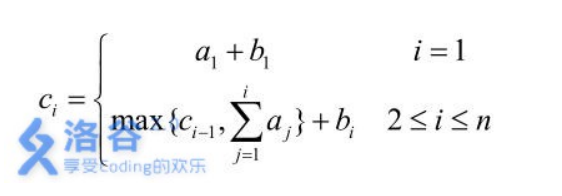
可以发现 a 的前缀和对 答案有一定的影响 ,所以相等时,把 a 小的放前面会是更优的一种选择;同样的,b 对答案肯定也有影响,每个 b 都会被计算一次,相等时,把 b 大的放前面会是更优的一种选择。那么现在可以得出两种解法(即两种正确决策):
===========================================================
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define rg register
#define ll long long
I ll rd()
{
ll x=0,f=0; char c=getchar();
while(!isdigit(c)){f|=c=='-';c=getchar();}
while( isdigit(c)){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
return f?-x:x;
}
const int N = 2E4+10;
struct node{
ll a,b;
bool operator < (const node& x)const{
return min(a,x.b)==min(x.a,b)?a<x.a:min(a,x.b)<min(x.a,b); //决策 1
return min(a,x.b)==min(x.a,b)?b>x.b:min(a,x.b)<min(x.a,b); //决策 2
}
}e[N];
int n;
int main()
{
int T=rd();
while(T--)
{
n=rd();
for(int i=1;i<=n;i++) e[i].a=rd(),e[i].b=rd();
sort(e+1,e+n+1);
ll sum=e[1].a+e[1].b,pre=e[1].a;
for(int i=2;i<=n;i++)
pre+=e[i].a,sum=max(sum,pre)+e[i].b;
printf("%lld\n",sum);
}
}
对于每一组\((a_{i},b_{j})\)两个元素之间的关系也影响着答案,我们试着建立
这里把所有元素分成了三类,按照 \(min(b_{i},a_{j}) \leqslant min(b_{j},a_{i})\) 来判断:
\(① d_{i} = d_{j} = -1 时,按照 a 升序排;\)
\(② d_{i} = d_{j} = 0 时,随意排;\)
\(③ d_{i} = d_{j} = 1 时,按照 b 降序排;\)
剩下的 \(d_{i} != d_{j}\) 的情况,都只要满足 \(d_{i} < d_{j}\) 就能满足 \(min(b_{j},a_{i}) \leqslant min(b_{i},a_{j})\),综上所述,新的决策不仅完全满足旧决策的约束,而且也满足了不可比性的传递性(不难发现,把元素分类之后,每类元素之间具有传递性,然后类与类之间也具有传递性),这样子就得到了第三种解法。
===========================================================
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define rg register
#define ll long long
I ll rd()
{
ll x=0,f=0; char c=getchar();
while(!isdigit(c)){f|=c=='-';c=getchar();}
while( isdigit(c)){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
return f?-x:x;
}
const int N = 2E4+10;
struct node{
ll a,b,d;
bool operator < (const node& x)const{
if(d==x.d)
{
if(d<=0) return a<x.a;
else return b>x.b;
}
return d<x.d;
}
}e[N];
int n;
int main()
{
int T=rd();
while(T--)
{
n=rd();
for(int i=1;i<=n;i++){
e[i].a=rd(),e[i].b=rd();
if(e[i].a<e[i].b) e[i].d=-1;
if(e[i].a==e[i].b) e[i].d=0;
if(e[i].a>e[i].b) e[i].d=1;
}
sort(e+1,e+n+1);
ll sum=e[1].a+e[1].b,pre=e[1].a;
for(int i=2;i<=n;i++)
pre+=e[i].a,sum=max(sum,pre)+e[i].b;
printf("%lld\n",sum);
}
}
Ⅲ:P1248 加工生产调度
分析: 这是典型的流水调度问题,用邻项交换的思想,我们先假设现在只有两件产品,加工所需时间分别是\((a_{i},b_{i})和(a_{j},b_{j})\),则
①若 i 在 j 前面,需要的时间是 \(a_i+max(a_j,b_i)+b_j\);
②若 i 在 j 后面,需要的时间是 \(a_j+max(a_i,b_j)+b_i\);
现在我们假设前一种方案更优,此时应有
移项
左右两边都等价于留下较小的相反数,即
消去负号最终得
同样的,这个决策肯定不满足 不可比性的传递性 ,解法和上一个题一样,不再赘述。
===========================================================
#include<bits/stdc++.h>
using namespace std;
#define I inline
#define rg register
#define ll long long
I ll rd()
{
ll x=0,f=0; char c=getchar();
while(!isdigit(c)){f|=c=='-';c=getchar();}
while( isdigit(c)){x=(x<<3)+(x<<1)+(c-48);c=getchar();}
return f?-x:x;
}
const int N = 2E4+10;
struct node{
ll a,b,d,id;
bool operator < (const node& x)const{
if(d==x.d)
{
if(d<=0) return a<x.a;
else return b>x.b;
}
return d<x.d;
}
}e[N];
int n;
int main()
{
n=rd();
for(int i=1;i<=n;i++) e[i].a=rd();
for(int i=1;i<=n;i++) e[i].b=rd();
for(int i=1;i<=n;i++){
e[i].id=i;
if(e[i].a<e[i].b) e[i].d=-1;
if(e[i].a==e[i].b) e[i].d=0;
if(e[i].a>e[i].b) e[i].d=1;
}
sort(e+1,e+n+1);
ll sum=e[1].a;
for(int i=2;i<=n;i++)
if(e[i].a>=e[i-1].b) sum+=e[i].a;
else e[i+1].a-=(e[i-1].b-e[i].a),sum+=e[i-1].b;
sum+=e[n].b;
printf("%lld\n",sum);
for(int i=1;i<=n;i++) printf("%d%c",e[i].id,i==n?'\n':' ');
}