作为数据分析师一定要知道的推断分析（参数估计）

推断统计是研究如何利用样本数据来推断总体特征的统计方法。参比如，要了解一个地区的人口特征，不可能对每个人的特征一一进行测量，对产品的质量进行检验，往往是破坏性的，也不可能对每个产品进行测量。这就需要抽取部分个体即样本进行测量，然后根据获得的样本数据对所研究的总体特征进行推断，这就是推断统计要解决的问题。

推断统计分析包括两方面的内容：
参数估计和假设检验。
本篇博客讲解的是推断分析中参数的估计，包括其含义与应用。

目标：

熟知点估计与区间估计的概念与区别。
熟知中心极限定理的含义。
熟知正态分布及其特征。

1、推断统计分析

（1）总体、个体与样本

总体：是包含我们要研究的所有数据，总体中的某个数据，就是个体。总体是所有个体构成的集合。从总体中抽取部分个体，就构成了样本，样本是总体的一个子集。样本中包含的个体数量，称为样本容量。

（2）推断统计

推断统计研究如何根据样本数据去推断总体数量特征的方法。它是对样本数据进行描述的基础上，对统计总体的未知数量特征做出以概率形式表述的推断。

我们为什么要进行推断呢？
因为在实际的研究中，获取总体数据通常比较困难，甚至也许是不可能完成的任务。因此，我们就需要对总体进行抽样，通过样本的统计量去估计总体参数。也就是说，总体的参数往往是未知的，我们为了获取总体的参数，就需要通过样本统计量，来估计总体参数。

2、点估计与区间

（1）点估计

就是使用样本的统计量去代替总体参数。
容易受到抽样的影响，造成误差。
例如：
我们要求鸢尾花的平均花瓣长度，就可以使用样本的均值来估计总体的均值。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
import warnings

# 设置seaborn绘图的样式。
# darkgrid 设置成暗色的网格的形式
sns.set(style="darkgrid")
# 设置字体
plt.rcParams["font.family"] = "SimHei"
# 对符号的支持
plt.rcParams["axes.unicode_minus"] = False
# 忽略警告信息。
warnings.filterwarnings("ignore")

# 加载鸢尾花数据集。
iris = load_iris()
# 将鸢尾花数据与对应的类型合并，组合成完整的记录。
data = np.concatenate([iris.data, iris.target.reshape(-1, 1)], axis=1)
data = pd.DataFrame(data, 
        columns=["sepal_length", "sepal_width", "petal_length", "petal_width", "type"])
print(data["petal_length"].mean())

data["petal_length"].mean()获取花瓣长度的均值。
结果：3.7580000000000027

点估计实现简单，但是容易受到随机抽样的影响，可能无法保证结论的准确性。但是，点估计并非完全一无是处，因为样本来自总体，样本还是能够体现出总体的一些特征。

（2）区间估计

区间估计根据样本的统计量，计算出一个可能的区间和概率（信息指数值），表示总体的参数会有多少概率位于该区间中。
区间估计指定的区间，我们称为置信区间。
区间估计指定的概率，我们称为置信度。
通俗的讲，置信度就是有多大把握认为总体的参数是在置信区间内。
例如：认为小张的年龄有90%的可能是在30-40之间，那么30-40就是置信区间，90%就是置信度。

例如，鸢尾花花瓣长度有70%得到可能性在3.4cm ~ 3.8cm，3.4cm ~ 3.8cm就是置信区间，而70%就是置信度。

（3）点估计和区间估计的区别

点估计与区间估计区别：

• 点估计是使用一个值来代替总体参数值。

  • 优点：能够给出具体的估计值。
  • 缺点：缺乏准确信。

• 区间估计是使用一个置信区间与置信度，表示总体参数有多少可能（置信度）会在该范围（置信区间）内。

  • 优点：能够给出合理的范围以及信息指数。
  • 缺点：不能给出具体的值。

小练习：

正确答案选CD
解析：A选项从可行性角度就是错的，因为想要计算总体是个非常难的任务，总体非常庞大，总体是在改变的，所以通常是无法计算总体的。
B选项区间越发确实越准确，但是在现实中没有意义，应该估计的更加合理而不是一味追求区间越大，失去了推断统计的价值。
C选项是对的，无论是点估计还是区间估计都无法保证准确性。
D选项正确，我们没办法依据总体进行计算，所以我们一般都会通过样本来计量。

我们经过抽样，获取一个样本后，该如何才能确定置信区间和置信度呢？

这时候我们就用到了中心极限定理。

3、中心极限定理

（1）定理内容

要确定置信区间和置信度，我们首先要知道总体与样本之间，在分布上有着怎样的联系。
在数学上，中心极限定理 给出了很好的解释说明，内容如下：
如果总体（分布不重要）均值为 μ，方差为 σ2，我们随机进行抽样，样本容量为n，当n增大时，则样本均值逐渐趋近服从正态分布：

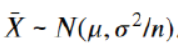
μ 总体均值
σ2 总体方差
σ 总体标准差
n 样本容量
μ 样本均值构成正态分布的均值
σ2/n 样本均值构成正态分布的方差
σ/√n 样本均值构成正态分布的标准差（标准误差/标准误）

我们可以得出以下结论：

1. 进行多次抽样，则每次抽样会得到一个均值，这些均值会围绕在总体均值左右，呈正态分布。
2. 当样本容量n足够大时，样本均值服从正态分布。 样本均值构成的正态分布，其均值等于总体均值 μ。 样本均值构成的正态分布，其标准差等于总体标准差 σ 除以√n。

标准误差（标准误）：无数个样本均值构成的正态分布，这个正态分布的标准差就是标准误差也就是标准误。σ/√n
总体的标准差：σ
样本的标准差：进行一次抽样所得到的标准差。

（2）程序模拟说明

#定义总体数据
#loc：均值
#scale：标准差
#size：数组的大小，即数组中含有元素的个数
#总体服从的正态分布数据：
all_ = np.random.normal(loc=30,scale=80,size=100000)
#创建均值数组，用来存放每个抽样（每个样本）的均值。
mean_arr = np.zeros(1000)
#循环1000次，获取1000个样本
for i in range(len(mean_arr)):
    #进行随机抽样。计算每个样本的均值，并放入数组中。
    #size：样本容量。
    #replace：是否为放回抽样，默认为True。
    #从总体中抽样choice
    mean_arr[i] = np.random.choice(all_,size=64,replace=False).mean()
#样本均值构成正态分布，该正态分布的均值等于总体的均值，该正态分布的标准差（标准误）等于总体的标准差/根号n
print("样本均值构的成正态分布--均值：",mean_arr.mean())
print("样本均值构的成正态分布--标准差（标准误）：",mean_arr.std())
print("偏度：",pd.Series(mean_arr).skew())
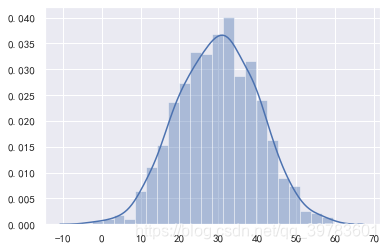
sns.distplot(mean_arr)

结果：

从结果可以看到，样本均值构成正态分布的均值为：29.99340859761859 和总体均值 30 非常接近。
样本均值构的成正态分布–标准差（标准误）为 10.226278999969239，而总体的标准差是80，样本均值构的成正态分布的标准差就是80除以根号64（64位样本容量）等于10，和10.226278999969239非常接近。
偏度 -0.031000713476693035 接近0。
所以这是个典型的正态分布。

4、正态分布的特性

（1）正态分布的特性

正态分布中，均值、中位数与众数是相等的。越靠近均值的数据越多，反之越少。

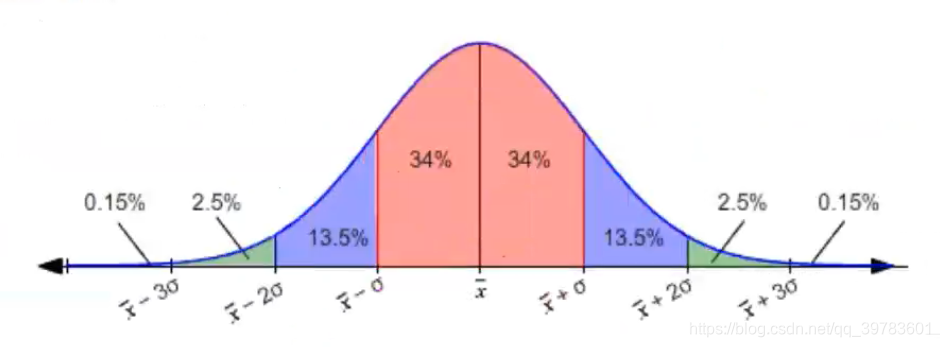
在正态分布中，数据的分布比例如下：

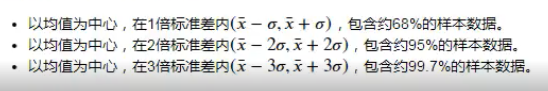
#定义一个标准差
scale = 50
#定义数据，均值为0
x = np.random.normal(0,scale,size=100000)
#定义标准差的倍数，倍数从1到3
for times in range(1,4):
    y = x[(x > -times * scale)&(x < times * scale)]
    print(f"{times}倍标准差：")
    print(f"{len(y) * 100 / len(x)}%")

解析： y = x[(x > -times * scale)&(x < times * scale)] 因为均值是0，所以这里省略不写；
np.random.normal 定义一个正态分布，参数分别为：均值、标准差、还有数据个数。

结果：

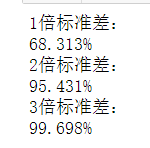
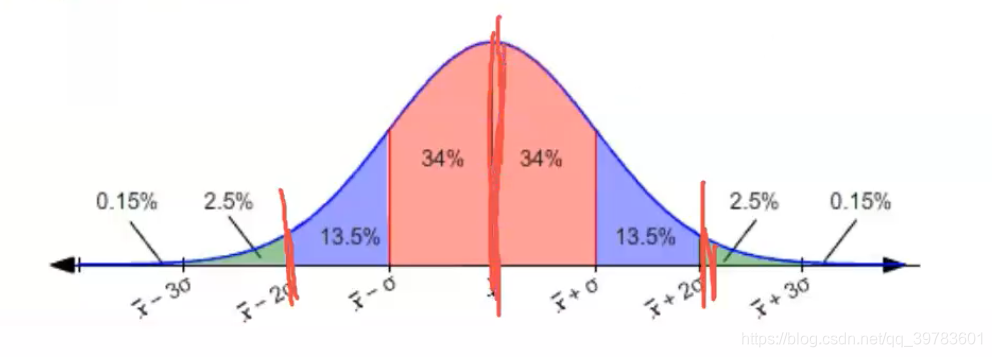
假如我们现在进行抽样（现实生活中我们只会进行一次抽样），我们进行一次抽样得到一个样本均值，一次抽样的均值就是无数个抽样均值中的一员，形成正态分布。那么这个一次抽样的均值是有95%的可能会落在以均值为中心2倍的标准差内。这个样本的均值是有95%的概率不会偏离这个正态分布的均值超过2倍的标准差的，也就意味着有95%的概率它会落在我们均值为中心正负2倍的标准差范围之内。

根据中心极限定理，我们能不能得到这样的一种结论呢？
样本均值构成的正态分布，正态分布的均值等于总体的均值，我们进行一次抽样得到的均值他不会偏离正态分布均值超过2倍的标准差的，言外之意就是样本均值95%的概率不会偏离总体超过2倍的标准差。

我们的目的就是通过样本的标准差推断总体是在哪个区间之内。
我们进行一次抽样得到一个样本均值，这个样本均值是无数个样本均值其中的一个，现在我们把样本均值视为中心加减2倍标准差，就有95%的概率涵盖总体。
所以置信区间是：

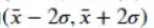
置信度：95%

疑问？
我们为什么是以2倍的标准差作为置信区间，而不是1倍或者3倍的呢？
因为2倍的标准差是正好合适的，如果我们要是以1倍的标准差作为衡量的话，对于这样的置信区间，根据正态分布的特性，置信度是68%，虽然说这个置信区间相对来说比较短（当然置信区间越短/小越好，因为越短总体的幅度才不是特别大，置信区间越长意义就不大了），但是置信度68%也不是特别高，往往不会更加有效的进行应用，因为它不在这个区间的还有32%的概率。所以我们想要提高置信度（提高概率）选择了2倍的标准差，在这个范围之下，我们可以涵盖95%的数据，这个置信度就够用了，也比较合适。如果说你觉得3倍的标准差置信度岂不是更高？是更高了，但是我们还要考虑置信区间的长度，变得太长就没有意义了，而且从2倍的标准差变为3倍的标准差也只是99.7%概率，只是增加了4.7%的置信度，但是置信区间却拉长了一倍，这样不划算。

我们通过一个练习来理解一下2倍标准差的公式中的参数：

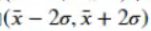
（2）程序模拟说明

# 使用随机数生成总体均值，其值未知。
mean = np.random.randint(-10000, 10000)
# 定义总体标准差。
std = 50
# 定义样本容量。
n = 50
# 随机生成总体数据。
all_ = np.random.normal(loc=mean, scale=std, size=10000)
# 从总体中抽取若干个体，构成一个样本。
sample = np.random.choice(all_, size=n, replace=False)
sample_mean = sample.mean()
print("总体的均值：", mean)
print("一次抽样的样本均值：", sample_mean)
plt.plot(mean, 0, marker="*", color="orange", ms=15, label="总体均值")
plt.plot(sample_mean, 0, marker="o", color="r", label="样本均值")
# 计算标准误差。
se = std / np.sqrt(n)
min_ = sample_mean - 1.96 * se
max_ = sample_mean + 1.96 * se
print("置信区间（95%置信度）：", (min_, max_))
plt.hlines(0, xmin=min_, xmax=max_, colors="b", label="置信区间")
plt.axvline(min_, 0.4, 0.6, color="r", ls="--", label="左边界")
plt.axvline(max_, 0.4, 0.6, color="g", ls="--", label="右边界")
plt.legend()

代码解析：
总体的均值是多少我们通过随机数生成 mean = np.random.randint(-10000, 10000)；
生成总体的数据也就是生成一个正态分布数据：all_ = np.random.normal(loc=mean, scale=std, size=10000)，总体数量是10000；
抽样，输出一次抽样的样本均值sample_mean和总体均值mean；
画出样本均值和总体均值（从结果图中可以看到）：
plt.plot(mean, 0, marker="*", color="orange", ms=15, label="总体均值") 总体均值在图中显示 橘色的 * ；
plt.plot(sample_mean, 0, marker="o", color="r", label="样本均值") 样本均值在图中显示为 红色的 o ；
计算置信区间：
min_ = sample_mean - 1.96 * se
max_ = sample_mean + 1.96 * se
用样本的均值加减2倍的标准差得到最大和最小值。

这里为什么写的是1.96而不是2呢 ？
其实2倍的标准差是涵盖了 超过 95%的数据，如果是更接近95%的话其实就是正负1.96的标准差。

plt.hlines 画一条线表示置信区间；
plt.axvline 画出他们的边界线，其中0.4和0.6代表按40%和60%显示，min和max就是置信区间最小值和最大值的坐标

结果：
总体的均值： 5863
一次抽样的样本均值： 5850.496792383608
置信区间（95%置信度）： (5836.637499472352, 5864.356085294865)

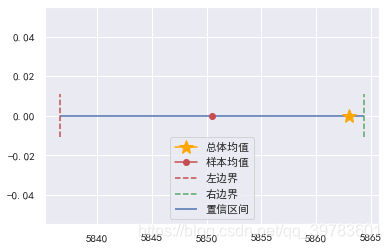
可以看到，样本均值95%的概率落在了2倍标准差的置信区间内。

5、放松一下

1、以下说法正确的是（ A ）
A 总体均值是有可能不在置信区间内的。
B 进行一次随机抽样，获取样本均值，则该样本均值会非常靠近总体均值。
C 从总体中多次抽样，样本均值分布为正态分布。
D 如果置信度为95%，则置信区间的长度约为2倍标准差。

解析：A选项正确，因为置信区间的置信度是95%，那么就有5%的可能总体均值是不在置信区间内的。
B选项错误，因为我们有5%的概率是超过2倍标准差的，所以样本均值可能会离总体均值非常远。
C选项错误，从严格意义上说（中心极限定理），只有在样本容量n 足够大的时候才会越来越趋近正态分布，通常n>=30 的时候才是正态分布。
D选项错误，如果置信度为95%，则置信区间的长度约为4倍标准差。（左2倍右2倍）

2、我们可以不用进行区间估计，因为样本容量较大时，样本均值分布呈现正态分布，其均值就等于总体的均值。所以，只要计算样本均值分布的均值，，就可以准确得出总体的均值了。这种说法正确吗？（ C ）
A 正确
B 不正确
C 正确，但不可行
D 不正确，但是可行

解析：C选项正确，要想获得正态分布，我们需要进行无数次的抽样，得到无数次抽样后的样本均值才等于总体的均值，这样的话是不可行的。

6、总结

• 推断性统计分析的概念与应用。
• 点估计与区间估计。
• 中心极限定理。
• 正态分布的特性。
• 置信区间与置信度的计算。