DFS序总结

其他 2020-04-15 03:20:38 阅读次数: 0

DFS序

对树进行 d f s dfs 遍历，所形成的序列就叫做树的 d f s dfs 序。
DFS序有一个很强的性质: 一颗子树的所有节点在DFS序内是连续的一段, 利用这个性质我们就可以将树形结构转化为线性结构 处理。

int in[N],ou[N];
int idx;int b[N];
void dfs(int x,int fa){
    in[x] = ++ idx;
    b[idx] = x;
    for(int i = head[x];i;i = edge[i].next){
        int y = edge[i].to;
        if(y == fa) continue;
        dfs(y,x);
    }
    ou[x] = idx;
}

poj 3321 Apple Tree
题意就是查询子树和 和 单调修改。

struct Edge
{
    int next;
    int to;
}edge[N<<1];
int head[N<<1],tot;
inline void add(int from,int to){
    edge[++tot].next = head[from];
    edge[tot].to = to;
    head[from] = tot;
}
int in[N],ou[N],idx,a[N];
void dfs(int x,int fa){
    in[x] = ++ idx;
    //cout<<in[x]<<endl;
    for(int i = head[x];i;i = edge[i].next){
        int y = edge[i].to;
        if(y!=fa) dfs(y,x);
    }
    ou[x] = idx;
    //cout<<ou[x]<<endl;
}
ll tree[N<<1];
void built(int rt,int l,int r){
    if(l == r){
        tree[rt] = 1;
        return ;
    }
    int mid = l + r >> 1;
    built(rt<<1,l,mid);
    built(rt<<1|1,mid+1,r);
    tree[rt] = tree[rt<<1] + tree[rt<<1|1];
}
void update(int p,int rt,int l,int r){
    if(l == r){
        tree[rt] ^= 1;
        return ;
    }
    int mid = l + r >> 1;
    if(p<=mid) update(p,rt<<1,l,mid);
    else update(p,rt<<1|1,mid+1,r);
    tree[rt] = tree[rt<<1] + tree[rt<<1|1];
}
ll query(int L,int R,int rt,int l,int r){
    if(L<=l&&r<=R){
        return tree[rt];
    }
    int mid = l + r >>1;
    ll ans = 0;
    if(L<=mid) ans += query(L,R,rt<<1,l,mid);
    if(R>mid) ans += query(L,R,rt<<1|1,mid+1,r);
    return ans;
}
int main(){
    int n = read();
    for(int i = 1;i <= n-1;++ i){
        int u = read(),v = read();
        add(u,v);
        add(v,u);
    }
    dfs(1,-1);
    built(1,1,idx);
    int q = read();
    char op[2];int x;
    while(q--){
        scanf("%s%d",op,&x);
        if(op[0] == 'Q') cout<<query(in[x],ou[x],1,1,idx)<<endl;
        else {
            update(in[x],1,1,idx);
        }
    }

}

欧拉序

以下转自Pealicx
树的欧拉序是对树进行DFS的一种序列。有两种形式：1、在每个结点进和出都加进序列。2、只要到达每一个结点就把他加进序列。

例如：给出一棵树：

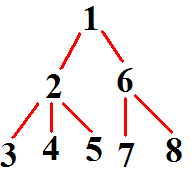
在这里插入图片描述

第一种方法得到的序列和对应的进出状态分别是：

1 2 3 3 4 4 5 5 2 6 7 7 8 8 6 1

进 进 进 出 进 出 进 出 出 进 进 出 进 出 出 出

（每个结点恰好出现了两次）

用这个序列可以解决树上求和的问题：

1、求某个点到根节点的点权值和。方法是：需要在进的点处做加法，出的点处做减法，查询某点就只需要查询对应的前缀即可。

*2、求某个子树的权值和。方法是：需要在进的点处做加法，求某个点最后一次出现的位置的前缀和减去第一次出现的位置的前一个位置的前缀和即可。

第二种方法得到的序列是：

1 2 3 2 4 2 5 2 1 6 7 6 8 6 1

用这一个序列，可以解决的一个问题是：

1、求某两点的LCA。显然这两点之间的区间中，深度最小点就是LCA。这可以用RMQ解决。

2、求某个子树的权值和，方法是：只记录第一次出现的数的值，同样的查询某点就只需要查询该点在欧拉序中最后出现的位置的前缀即可减去第一次出现的额位置-1的前缀和即可。

3、换根操作：这种欧拉序相当于以根为起点围着树跑了一圈，那么我们就可以把欧拉序写成一个环就是：

1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6

以某个点为跟的欧拉序就是以某个点在上面的欧拉序中第一次出现的位置为起点向前走（2*n-1）步，例如以4为根的欧拉序就是

1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6

      \ \\ \ \ \ \qquad L-------------------------------------------------R//以4为跟的欧拉序，同时可以维护和之类的东西。

int in[N],ou[N];
int idx;int b[N];
void dfs(int x,int fa){
    in[x] = ++idx;
    b[idx] = x;
    vis[idx] = 0;//标记入点
    for(int i = head[x];i;i = edge[i].next){
        int y = edge[i].to;
        if(y == fa) continue;
        dfs(y,x);
    }
    ou[x] = ++idx;
    b[idx] = x;
    vis[idx] = 1;//标记出点
}

bzoj4034: [HAOI2015]树上操作
在这里插入图片描述
思路：
欧拉序维护到根的点权和。在入点加，出点减。这样，求某个节点到根路径上的点权和时，直接对区间 [ 1 , i n [ x ] ] [1,in[x]] 求和即可。而1,2操作其实就是区间加。
因为有对区加的修改，所以我们可定要用懒标记，可是一个区间中入点是正的，出点是负的，我们进行区间修改时似乎没法操作。那么我们在引入 c n t [ i ] cnt[i] ，表示 i i 节点所代表的区间中有多少个出点(负)。那么区间修改，就是当前节点 加上 ( r − l + 1 − 2 ∗ c n t [ r t ] ) ⋅ l z y [ r t ] (r-l+1 - 2*cnt[rt])\cdot lzy[rt] ，为什么要减去二倍呢，是以为负的有 c n t [ r t ] cnt[rt] 个，那么正的就是 r − l + 1 − c n t [ r t ] r-l+1-cnt[rt] 个，然后两者做差就是区间的增量了。这里debug好大会。。。。一定要注意。同理，懒标记的下放也是如此。

struct Edge
{
    int next;
    int to;
}edge[N<<1];
int head[N],tot;
int in[N],ou[N];
ll a[N],b[N];bool vis[N];
inline void add(int from,int to ){
    edge[++tot].next = head[from];
    edge[tot].to = to;
    head[from] = tot;
}
ll tree[N<<2];int cnt[N<<2];ll lzy[N<<2];
inline void push_down(int rt,int len){
    tree[rt<<1] += 1LL*(len-(len>>1)-2*cnt[rt<<1])*lzy[rt];
    lzy[rt<<1] += lzy[rt];
    tree[rt<<1|1] += 1LL*((len>>1) - 2*cnt[rt<<1|1])*lzy[rt];
    lzy[rt<<1|1] += lzy[rt];
    lzy[rt] = 0;
}
void built(int rt,int l,int r){
    if(l == r) {
        if(vis[l]) tree[rt] = -a[b[l]],cnt[rt] ++;
        else tree[rt] = a[b[l]];
        return ;
    }
    int mid = l + r >> 1;
    built(rt<<1,l,mid);
    built(rt<<1|1,mid+1,r);
    tree[rt] = tree[rt<<1] + tree[rt<<1|1];
    cnt[rt] = cnt[rt<<1] + cnt[rt<<1|1];
}
int idx;
void dfs(int x,int fa){
    in[x] = ++idx;
    b[idx] = x;
    vis[idx] = 0;//标记入点
    for(int i = head[x];i;i = edge[i].next){
        int y = edge[i].to;
        if(y == fa) continue;
        dfs(y,x);
    }
    ou[x] = ++idx;
    b[idx] = x;
    vis[idx] = 1;//标记出点
}
void update(int L,int R,int dat,int rt,int l,int r){
    if(L<=l&&r<=R){
        tree[rt] += 1LL*(r-l+1 - 2*cnt[rt])*dat;
        lzy[rt] += dat;
        return ;
    }
    if(lzy[rt]) push_down(rt,r-l+1);
    int mid = l + r >> 1;
    if(L <= mid) update(L,R,dat,rt<<1,l,mid);
    if(R>mid) update(L,R,dat,rt<<1|1,mid + 1,r);
    tree[rt] = tree[rt<<1] + tree[rt<<1|1];
}
ll query(int L,int R,int rt,int l,int r){
    if(L<=l&&r<=R){
        return tree[rt];
    }
    if(lzy[rt]) push_down(rt,r-l+1);
    int mid = l + r >> 1;
    ll ans = 0;
    if(L <= mid) ans += query(L,R,rt<<1,l,mid);
    if(R>mid) ans += query(L,R,rt<<1|1,mid+1,r);
    return ans;
}
int main(){
    int n,m;
    n = read(),m = read();
    rep(i,1,n) a[i] = read();
    rep(i,1,n-1) {
        int u = read(),v = read();
        add(u,v);
        add(v,u);
    }
    dfs(1,0);//预处理欧拉序
    built(1,1,idx);
    rep(i,1,m){
        int op = read();
        if(op == 1){
            int p = read(),d = read();
            update(in[p],in[p],d,1,1,idx);
            update(ou[p],ou[p],d,1,1,idx);
        }
        else if(op==2){
            int p = read(),d = read();
            update(in[p],ou[p],d,1,1,idx);
        }
        else {
            int p = read();
            printf("%lld\n",query(1,in[p],1,1,idx));
        }
    }

}

hdu5692 Snacks
题意：
给你一棵树，然后每个点都有个点权，然后有两个操作。
0 x y 单点修改
1 x 查询经过 x x 的到根的路径中，权值和最大的路径值。
思路：
关于 1    x 1 \ \ x 操作就是查看以 x x 为根的子树中，到根路径上最大权值和。我们可以参考上面那道题，跑出欧拉序， i n [ x ] in[x] 代表 x x 的入栈编号， o u [ x ] ou[x] 代表 x x 的出栈编号，我们让欧拉序列中 入栈加权值，出栈减权值，以此预处理欧拉序列前缀和，那么前缀和数组中以 i n [ x ] in[x] 为下标代表 x x 到根的权值和，然后用线段树维护前缀和数组。
查询 以 x x 为根的子树中到根节点权值和的最大值，就是查询线段树中 [ i n [ x ] , o u [ x ] − 1 ] [in[x],ou[x]-1] 最大值。为什么是 o u [ x ] − 1 ou[x]-1 ，是因为出栈减权值，所以 o u [ x ] ou[x] 并不在子树中。这个操作对线段树来说小case。

然后单点修改点权，因为线段树维护的是前缀和，我们我们要在线段树中区间修改，将 x x 点权改为 y y ，就是 [ i n x [ x ] , i d x ] [inx[x],idx] 这个序列 − a [ x ] + y -a[x]+y ， [ o u [ x ] , i d x ] [ou[x],idx] 这个序列 − ( − a [ x ] ) − y -(-a[x])-y 。

这样就 o k ok 了，然而我忘记下放标记导致Wa了挺久，但是我相信我的思路没错，终于AC了，好棒！。

struct Edge
{
    int next;
    int to;
}edge[N<<1];
int head[N],tot;
inline void add(int from,int to){
    edge[++tot].next = head[from];
    edge[tot].to = to;
    head[from] = tot;
}
int in[N<<1],ou[N<<1],idx,a[N<<1],b[N<<1];ll c[N<<1];
ll Max[N<<2];ll lzy[N<<2];bool vis[N<<1];
void dfs(int x,int fa){
    in[x] = ++idx;
    b[idx] = x;
    for(int i = head[x];i;i = edge[i].next){
        int y = edge[i].to;
        if(y!=fa) dfs(y,x);
    }
    ou[x] = ++ idx;
    vis[idx] = 1;
    b[idx] = x;
}
void push_down(int rt){//下放标记
    Max[rt<<1] += lzy[rt];
    Max[rt<<1|1] += lzy[rt];
    lzy[rt<<1] += lzy[rt];
    lzy[rt<<1|1] += lzy[rt];
    lzy[rt] = 0;
}
void built(int rt,int l,int r){
    lzy[rt] = 0;Max[rt] = 0;
    if(l == r) {
        Max[rt] = c[l];
        return ;
    }
    int mid = l + r >> 1;
    built(rt<<1,l,mid);
    built(rt<<1|1,mid+1,r);
    Max[rt] = max(Max[rt<<1],Max[rt<<1|1]);
}
void update(int L,int R,int dat,int rt,int l,int r){
    if(L<=l&&r<=R){
        Max[rt] += dat;
        lzy[rt] += dat;
        return ;
    }
    if(lzy[rt]) push_down(rt);
    int mid = l + r>>1;
    if(L<=mid) update(L,R,dat,rt<<1,l,mid);
    if(R>mid) update(L,R,dat,rt<<1|1,mid+1,r);
    Max[rt] = max(Max[rt<<1],Max[rt<<1|1]);
}
ll query(int L,int R,int rt,int l,int r){
    if(L<=l&&r<=R) return Max[rt];
    if(lzy[rt]) push_down(rt);
    int mid = l + r >>1;
    ll ans = -1e15;
    if(L<=mid) ans = max(ans,query(L,R,rt<<1,l,mid));
    if(R>mid) ans = max(ans,query(L,R,rt<<1|1,mid+1,r));
    return ans; 
}
inline void init(int n){
    memset(vis,0,sizeof vis);
    memset(head,0,sizeof head);
    tot = idx = 0;
}
int main(){
    int t = read();
    rep(Case,1,t){
        int n = read(),m = read();
        init(n);
        rep(i,1,n-1){
            int u = read(),v = read();
            u ++ ,v ++;
            add(u,v);
            add(v,u);
        }
        dfs(1,-1);//跑欧拉序
        for(int i = 1;i <= n;++i) a[i] = read();
        for(int i = 1;i <= idx;++i){    //预处理 欧拉序列前缀和
            int tmp = b[i];
            if(vis[i]) c[i] = c[i-1] - a[tmp];
            else c[i] = c[i-1] + a[tmp];
        }
        built(1,1,idx);
        printf("Case #%d:\n",Case);
        while(m--){
            int op = read();
            if(op == 0){
                int u = read(),v = read();
                u ++;
                update(in[u],idx,v-a[u],1,1,idx);
                update(ou[u],idx,a[u]-v,1,1,idx);
                a[u] = v;//别忘了
            }
            else {
                int u = read();
                u ++;
                printf("%lld\n",query(in[u],ou[u]-1,1,1,idx));
            }
        }
    }
}

写在最后

DFS序的七个经典问题

给定一棵树，每个点都有权值，且不妨假设根节点为1

1、单点更新，查询以 x x 为根的子树的 权值和。

​ 由于DFS序的性质，上述问题就转化为了单点更新，区间查询，树状数组或者线段树维护即可。

2、对树上 x x 到 y y 节点 路径上的点的权值加上一个 W W ,查询某个点的权值。

x − > y x->y 路径上的点加 W W ，其实就是 x x 到 根节点1的路径上 加一个 W W , y y 到根节点1的路径上加一个 W W ， l c a ( x , y ) lca(x,y) 到根的路径上减去一个 W W , f a [ l c a ( x , y ) ] fa[lca(x,y)] 到根的路径减去一个 W W 。那么我们考虑树上差分， d [ x ] + = W , d [ y ] + = w , d [ l c a ( x , y ) ] − = w , d [ f a [ l c a ( x , y ) ] ] − = w d[x]+=W,d[y]+=w,d[lca(x,y)]-=w,d[fa[lca(x,y)]] -=w ,那么我们查询 u u 的权值时，就是 a [ u ] a[u] 加上 u u 子树上增加的权值和。

也就是转化为第一个问题。

3、对树上 x − > y x->y 的路径点加一个 W W ，询问以 u u 为根节点的子树权值和。

和上个题目有些许类似，只不过上个题目的单点查询改为了查询子树和。

我们依旧用 d d 数组进行树上差分。先考虑 u u 的某个子树中的节点 i i ，它对结果产生的贡献就是 d [ i ] ⋅ ( d e p t h [ i ] − d e p t h [ u ] ) d[i]\cdot (depth[i]-depth[u]) ,也就是 i i 到路径上的节点个数乘以个 d [ i ] d[i] ,这是可能会些疑惑， 如果 f a [ l c a ( x , y ) fa[lca(x,y) 节点在 u u 上面，那么这样肯定是对的，如果在 u u 的子树中，那么 f a [ l c a ( x , y ) ] fa[lca(x,y)] 产生的贡献会抵消掉 i i 多产生的贡献，和差分的道理是一样的。

然后 d [ i ] ⋅ ( d e p t h [ i ] − d e p t h [ u ] + 1 ) d[i]\cdot (depth[i]-depth[u]+1) 不能用线段树维护，我们变一下型。

= d [ i ] ⋅ d e p t h [ i ] − d [ i ] ⋅ ( d e p t h [ u ] − 1 ) =d[i]\cdot depth[i] - d[i]\cdot (depth[u]-1)

这样我们就转化为问题2了，用线段树或者树状数组维护$d[i]\cdot depth[i] $ 和 d [ i ] d[i] 就行了。

4、对某个点 x x 权值加上一个数 W W ,查询 x x 到 y y 上路径上所有点权值之和。 感觉这儿用欧拉序，查询就是分别求出 x x 和 y y 到根节点的权值和，然后相加减去 l c a ( x , y ) lca(x,y) 到根节点的权值和。修改就是 i n [ x ] + = w , o u [ x ] − = w in[x]+=w,ou[x]-=w

5、对子树 x x 里所有节点上加上一个权值 w w ,查询某个点的权值。

区间修改，单点查询

6、对子树 x x 里所以皮节点加上一个 W W ，查询某个子树 x x 里所有结点权值之和。

区间更新，区间查询。

7、对子树 x x 里所有结点加上一个权值 W W ,查询 x x 到 y y 路径上的权值和。

利用欧拉序，转化为区间更新，区间查询。区间查询类似于问题 4 4

以上只是个人参考<<数据结构漫谈>> 所写，部分属于个人理解，感觉可行的方案，抽空把代码补上。

冷血怪兽
发布了636 篇原创文章 · 获赞 38 · 访问量 6万+
他的留言板 关注

猜你喜欢

转载自blog.csdn.net/qq_43408238/article/details/105224898
今日推荐
基于大语言模型的开源知识库问答系统 MaxKB GitHub Star 数量突破 5,000 个！
美国拟限制 AI 大模型出口中国和俄罗斯
苹果将与 OpenAI 达成协议，将 ChatGPT 应用于 iPhone
openKylin 社区生态委员会第六次会议圆满召开
阿里云正式发布通义千问 2.5
Python 3.13 发布首个 Beta：实验性自由线程模式和 JIT、改进交互式解释器
Stack Overflow 拿我的代码去训练 AI 大模型，还封了我的账号
Pop!_OS 的 COSMIC 桌面完成 App Store 上架工作
《2024 年一季度互联网投融资运行情况》研究报告
报告：Django 仍然是 74% 开发者的首选
15 年前上了“FFmpeg 耻辱柱”，今天他还得谢谢咱——腾讯QQPlayer一雪前耻？
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
周排行
记一下去大梅沙的准备（2018-05-26）
Spring 注解 事务
基于HTTP协议的客户端缓存
阿里云rds 备份和还原
[PHP] 几个拖慢 PHP 程序/API 运行速度的点
python 代码风格------------PEP8规则
js控制json生成菜单——自制菜单（一）
将字符串: 'k:1|k1:2|k2:3|k3:4 ' ,处理成 python 字典: {'k':1, 'k1':2, ...}
微信小程序转支付宝小程序
Qt551.窗口滚动条
每日归档
更多
2024-05-13(18)
2024-05-12(0)
2024-05-11(38)
2024-05-10(38)
2024-05-09(35)
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022