【恋上数据结构】图代码实现、BFS、DFS、拓扑排序、最小生成树（Prim、Kruskal）

图的基础代码

图的基础接口

package com.mj.graph;

import java.util.List;

public interface Graph<V, E> {
	int edgesSize(); 		// 边的数量
	int verticesSize();		// 顶点数量
	
	void addVertex(V v); 		// 添加顶点
	void addEdge(V from, V to); // 添加边
	void addEdge(V from, V to, E weight);// 添加边
	
	void removeVertex(V v); 		// 删除顶点
	void removeEdge(V from, V to);	 // 删除边
	
	interface vertexVisitor<V>{
		boolean visit(V v);
	}
	
 }

顶点Vertex

/**
* 顶点
 */
private static class Vertex<V, E> {
	V value;
	Set<Edge<V, E>> inEdges = new HashSet<>(); // 进来的边
	Set<Edge<V, E>> outEdges = new HashSet<>(); // 出去的边
	public Vertex(V value){
		this.value = value;
	}
	@Override
	public boolean equals(Object obj) {
		return Objects.equals(value, ((Vertex<V, E>)obj).value);
	}
	@Override
	public int hashCode() {
		return value == null ? 0 : value.hashCode();
	}
	@Override
	public String toString() {
		return value == null ? "null" : value.toString();
	}
	
}

边Edge

/*
 * 边
 */
private static class Edge<V, E> {
	Vertex<V, E> from; // 出发点
	Vertex<V, E> to; // 到达点
	E weight;	// 权值
	
	public Edge(Vertex<V, E> from, Vertex<V, E> to) {
		this.from = from;
		this.to = to;
	}
	@Override
	public boolean equals(Object obj) {
		Edge<V, E> edge = (Edge<V, E>) obj;
		return Objects.equals(from, edge.from) && Objects.equals(to, edge.to);
	}
	@Override
	public int hashCode() {
		return from.hashCode() * 31 + to.hashCode();
	}
	@Override
	public String toString() {
		return "Edge [from=" + from + ", to=" + to + ", weight=" + weight + "]";
	}
	
}

一些稍微复杂的操作单独列出来，简单地操作直接从完整源码中查看即可。

添加边addEdge

/**
 * 添加无权值的边
 */
@Override
public void addEdge(V from, V to) {
	addEdge(from, to, null);
}

/*
 * 添加有权值的边
 */
@Override
public void addEdge(V from, V to, E weight) {
	// 根据传入的参数from找到出发点,如果不存在则创建
	Vertex<V, E> fromVertex = vertices.get(from);
	if(fromVertex == null){ 
		fromVertex = new Vertex<>(from);
		vertices.put(from, fromVertex);
	}
	// 根据传入的参数to找到终点,如果不存在则创建
	Vertex<V, E> toVertex = vertices.get(to);
	if(toVertex == null){
		toVertex = new Vertex<>(to);
		vertices.put(to, toVertex);
	}
	
	// 根据出发点与终点,创建边
	Edge<V, E> edge = new Edge<>(fromVertex, toVertex);
	edge.weight = weight; // 有权值则加上权值,无权值则为null
	
	// 不管原来是否存在,都先删除此边,再添加进去
	if(fromVertex.outEdges.remove(edge)){ 
		toVertex.inEdges.remove(edge);
		edges.remove(edge);
	}
	fromVertex.outEdges.add(edge);
	toVertex.inEdges.add(edge);
	edges.add(edge);
}

删除边removeEdge

/*
 * 删除边
 */
@Override
public void removeEdge(V from, V to) {
	// 根据传入的from获得起点,不存在则不需要删除
	Vertex<V, E> fromVertex = vertices.get(from);
	if(fromVertex == null) return;
	// 根据传入的to找到终点,不存在则不需要删除
	Vertex<V, E> toVertex = vertices.get(to);
	if(toVertex == null) return;
	
	// 根据起点和终点获得边,然后删除
	Edge<V, E> edge = new Edge<>(fromVertex, toVertex);
	if(fromVertex.outEdges.remove(edge)){
		toVertex.inEdges.remove(edge);
		edges.remove(edge);
	}
}

删除点removeVertex

/*
 * 删除点
 */
@Override
public void removeVertex(V v) {
	// 根据传入的值找到点并删除,不存在则不做操作
	Vertex<V, E> vertex = vertices.remove(v);
	if(vertex == null) return;
	
	// 迭代器遍历集合vertex.outEdges
	for (Iterator<Edge<V, E>> iterator = vertex.outEdges.iterator(); iterator.hasNext();) {
		Edge<V, E> edge = iterator.next(); // 遍历到的该点出去的边
		edge.to.inEdges.remove(edge);// 获取终点进入的边,并从中删除遍历到的边
		iterator.remove(); // 将当前遍历到的元素edge从集合vertex.outEdges中删掉
		edges.remove(edge);
	}
	
	// 迭代器遍历集合vertex.inEdges
	for (Iterator<Edge<V, E>> iterator = vertex.inEdges.iterator(); iterator.hasNext();) {
		Edge<V, E> edge = iterator.next(); // 遍历到的进入该点的边
		edge.from.outEdges.remove(edge); // 获取起点出去的边,并从中删除遍历到的边
		iterator.remove(); // 将当前遍历到的元素edge从集合vertex.inEdges中删掉
		edges.remove(edge);
	}
	
}

完整源码

/**
 * 邻接表实现图
 */
@SuppressWarnings("unchecked")
public class ListGraph<V, E> implements Graph<V, E> {
	// 传入的V与顶点类Vertex的映射
	private Map<V, Vertex<V, E>> vertices = new HashMap<>();
	// 边的Set集合
	private Set<Edge<V, E>> edges = new HashSet<>();
	
	/**
	 * 顶点
	 */
	private static class Vertex<V, E> {
		V value;
		Set<Edge<V, E>> inEdges = new HashSet<>(); // 进来的边
		Set<Edge<V, E>> outEdges = new HashSet<>(); // 出去的边
		public Vertex(V value){
			this.value = value;
		}
		@Override
		public boolean equals(Object obj) {
			return Objects.equals(value, ((Vertex<V, E>)obj).value);
		}
		@Override
		public int hashCode() {
			return value == null ? 0 : value.hashCode();
		}
		@Override
		public String toString() {
			return value == null ? "null" : value.toString();
		}
		
	}
	/**
	 * 边
	 */
	private static class Edge<V, E> {
		Vertex<V, E> from; // 出发点
		Vertex<V, E> to; // 到达点
		E weight;	// 权值
		
		public Edge(Vertex<V, E> from, Vertex<V, E> to) {
			this.from = from;
			this.to = to;
		}
		@Override
		public boolean equals(Object obj) {
			Edge<V, E> edge = (Edge<V, E>) obj;
			return Objects.equals(from, edge.from) && Objects.equals(to, edge.to);
		}
		@Override
		public int hashCode() {
			return from.hashCode() * 31 + to.hashCode();
		}
		@Override
		public String toString() {
			return "Edge [from=" + from + ", to=" + to + ", weight=" + weight + "]";
		}
		
	}
	
	public void print(){
		System.out.println("[顶点]-------------------");
		vertices.forEach((V v, Vertex<V, E> vertex) -> {
			System.out.println(v);
			System.out.println("out-----------");
			System.out.println(vertex.outEdges);
			System.out.println("int-----------");
			System.out.println(vertex.inEdges);
		});
		System.out.println("[边]-------------------");
		edges.forEach((Edge<V, E> edge) -> {
			System.out.println(edge);
		});
	}
	
	@Override
	public int edgesSize() {
		return edges.size();
	}

	@Override
	public int verticesSize() {
		return vertices.size();
	}

	@Override
	public void addVertex(V v) {
		if(vertices.containsKey(v)) return;
		vertices.put(v, new Vertex<>(v));
	}

	@Override
	public void addEdge(V from, V to) {
		addEdge(from, to, null);
	}

	@Override
	public void addEdge(V from, V to, E weight) {
		// 根据传入的参数from找到起点,如果不存在则创建
		Vertex<V, E> fromVertex = vertices.get(from);
		if(fromVertex == null){ 
			fromVertex = new Vertex<>(from);
			vertices.put(from, fromVertex);
		}
		// 根据传入的参数to找到终点,如果不存在则创建
		Vertex<V, E> toVertex = vertices.get(to);
		if(toVertex == null){
			toVertex = new Vertex<>(to);
			vertices.put(to, toVertex);
		}
		
		// 根据出发点与终点,创建边
		Edge<V, E> edge = new Edge<>(fromVertex, toVertex);
		edge.weight = weight; // 有权值则加上权值,无权值则为null
		
		// 不管原来是否存在,都先删除此边,再添加进去
		if(fromVertex.outEdges.remove(edge)){ 
			toVertex.inEdges.remove(edge);
			edges.remove(edge);
		}
		fromVertex.outEdges.add(edge);
		toVertex.inEdges.add(edge);
		edges.add(edge);
	}
	
	@Override
	public void removeVertex(V v) {
		// 根据传入的值找到点并删除,不存在则不做操作
		Vertex<V, E> vertex = vertices.remove(v);
		if(vertex == null) return;
		
		// 迭代器遍历集合vertex.outEdges
		for (Iterator<Edge<V, E>> iterator = vertex.outEdges.iterator(); iterator.hasNext();) {
			Edge<V, E> edge = iterator.next(); // 遍历到的该点出去的边
			edge.to.inEdges.remove(edge);// 获取终点进入的边,并从中删除遍历到的边
			iterator.remove(); // 将当前遍历到的元素edge从集合vertex.outEdges中删掉
			edges.remove(edge);
		}
		
		// 迭代器遍历集合vertex.inEdges
		for (Iterator<Edge<V, E>> iterator = vertex.inEdges.iterator(); iterator.hasNext();) {
			Edge<V, E> edge = iterator.next(); // 遍历到的进入该点的边
			edge.from.outEdges.remove(edge); // 获取起点出去的边,并从中删除遍历到的边
			iterator.remove(); // 将当前遍历到的元素edge从集合vertex.inEdges中删掉
			edges.remove(edge);
		}
		
	}

	@Override
	public void removeEdge(V from, V to) {
		// 根据传入的from获得起点,不存在则不需要删除
		Vertex<V, E> fromVertex = vertices.get(from);
		if(fromVertex == null) return;
		// 根据传入的to找到终点,不存在则不需要删除
		Vertex<V, E> toVertex = vertices.get(to);
		if(toVertex == null) return;
		
		// 根据起点和终点获得边,然后删除
		Edge<V, E> edge = new Edge<>(fromVertex, toVertex);
		if(fromVertex.outEdges.remove(edge)){
			toVertex.inEdges.remove(edge);
			edges.remove(edge);
		}
	}
}

图的遍历

图的遍历

• 从图中某一顶点出发访问图中其余顶点，且每一个顶点仅被访问一次

图有2种常见的遍历方式（有向图、无向图都适用）

• 广度优先搜索（Breadth First Search，BFS），又称为宽度优先搜索、横向优先搜索。
• 深度优先搜索（Depth First Search，DFS）
  发明“深度优先搜索”算法的2位科学家在1986年共同获得计算机领域的最高奖：图灵奖。

在接口中增加 bfs 与 dfs 方法。

package com.mj.graph;

import java.util.List;

public interface Graph<V, E> {
	int edgesSize(); // 边的数量
	int verticesSize();	// 顶点数量
	
	void addVertex(V v); // 添加顶点
	void addEdge(V from, V to); // 添加边
	void addEdge(V from, V to, E weight);// 添加边
	
	void removeVertex(V v); // 删除顶点
	void removeEdge(V from, V to); // 删除边
	
	void bfs(V begin, vertexVisitor<V> visitor); // 广度优先搜索
	void dfs(V begin, vertexVisitor<V> visitor); // 深度优先搜索
	
	List<V> topologicalSort(); // 拓扑排序
	
	interface vertexVisitor<V>{
		boolean visit(V v);
	}
	
 }

广度优先搜索（Breadth First Search）思路与实现

之前所学的二叉树层序遍历就是一种广度优先搜索。

注：BFS结果不唯一。


思路：

从某个点开始，将它可以到达的点放入队列，如果已经访问过则跳过，然后从队列中取出点重复该过程。

• 第一层：假设从点A开始，它可以到达B、F，则将B、F入队。
  此时队列中元素 [B、F]
• 第二层：队头B出队，B可以到达C、I、G，将C、I、G入队。
  此时队列中元素 [F、C、I、G]
• 第三层：队头F出队，F可以到达G、E，但G已访问过，将E入队。
  此时队列中元素 [C、I、G、E]
• 第四层：队头C出队，C可以到达I、D，但I已访问过，将D入队。
• 此时队列中元素 [I、G、E、D]
• 第五层：队头I出队，I可以到达D，但D已访问过，不执行操作。
  此时队列中元素 [G、E、D]
• 第六层：队头G出队，G可以到达D、H，但D已访问过，将H入队。
  此时队列中元素 [E、D、H]
• 第七层：队头E出队，E可以到达D、H、F，都访问过，不执行操作。
  此时队列中元素 [D、H]
• 第八层：队头D出队，D可以到达C、H、E，都访问过，不执行操作。
  此时队列中元素 [H]
• 第九层：队头H出队，H可以到达D、G、E，都访问过，不执行操作。
  此时队列中元素 []
• 队列为空，广度优先搜索结束。

实现：

/**
 * 广度优先搜索BFS
 */
public void bfs(V begin, vertexVisitor<V> visitor) {
	if(visitor == null) return;
	// 根据传入的值begin找到顶点
	Vertex<V, E> beginVertex = vertices.get(begin);
	if(beginVertex == null) return; // 该顶点不存在,不做操作
	
	// 存放已经访问过的节点
	Set<Vertex<V, E>> visitedVertices = new HashSet<>();		
	Queue<Vertex<V, E>> queue = new LinkedList<>();
	queue.offer(beginVertex); // 元素入队
	visitedVertices.add(beginVertex);
	
	// 思路参考二叉树层次遍历,队列存放每一层的顶点,用集合记录已经访问过的点
	while(!queue.isEmpty()){
		Vertex<V, E> vertex = queue.poll(); // 队列中取出一个顶点
		if(visitor.visit(vertex.value)) return;
		// 遍历[队列中取出的顶点]的出去的边,将[这些边的终点]入队,并且标记为已经访问过
		for(Edge<V, E> edge : vertex.outEdges){
			// 如果集合中已经记录该顶点,说明已经访问过,跳过进行下一轮
			if(visitedVertices.contains(edge.to)) continue;
			queue.offer(edge.to);
			visitedVertices.add(edge.to);
		}
	}
	
}

深度优先搜索（Depth First Search）

之前所学的二叉树前序遍历就是一种深度优先搜索。

注：DFS结果不唯一。

递归实现

/**
 * 递归实现深度优先搜索DFS
 */
public void dfs(V begin) {
	Vertex<V, E> beginVertex = vertices.get(begin); // 根据传入的值获取顶点
	if (beginVertex == null) return; // 顶点不存在则不执行操作
	dfs2(beginVertex, new HashSet<>()); // 传入的集合,用来记录访问过的顶点
}
private void dfs(Vertex<V, E> vertex, Set<Vertex<V, E>> vistedVertices){
	System.out.println(vertex.value);
	vistedVertices.add(vertex);
	
	for(Edge<V, E> edge : vertex.outEdges){
		if(vistedVertices.contains(edge.to)) continue;
		dfs2(edge.to, vistedVertices);
	}
}

非递归思路与实现

/**
 * 非递归实现深度优先搜索DFS
 */
public void dfs(V begin, vertexVisitor<V> visitor){
	if(visitor == null) return;
	
	Vertex<V, E> beginVertex = vertices.get(begin);
	if(begin == null) return;
	
	Set<Vertex<V, E>> visitedVertices = new HashSet<>();
	Stack<Vertex<V, E>> stack = new Stack<>();
	
	stack.push(beginVertex); // 先访问起点
	visitedVertices.add(beginVertex);
	if(visitor.visit(begin)) return;
	
	while(!stack.isEmpty()){
		Vertex<V, E> vertex = stack.pop();
		
		for(Edge<V, E> edge : vertex.outEdges){
			if(visitedVertices.contains(edge.to)) continue;
			
			stack.push(edge.from);
			stack.push(edge.to);
			visitedVertices.add(edge.to);
			if(visitor.visit(edge.to.value)) return;
			
			break;
		}
	}
}

AOV网（Activity On Vertex Network）

一项大的工程常被分为多个小的子工

• 子工程之间可能存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始。

在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，子工程被称为活动（Activity）

• 以顶点表示活动、有向边表示活动之间的先后关系，这样的图简称为 AOV 网。

标准的AOV网必须是一个有向无环图（Directed Acyclic Graph，简称 DAG）

拓扑排序（Topological Sort）

前驱活动：有向边起点的活动称为终点的前驱活动

• 只有当一个活动的前驱全部都完成后，这个活动才能进行

后继活动：有向边终点的活动称为起点的后继活动

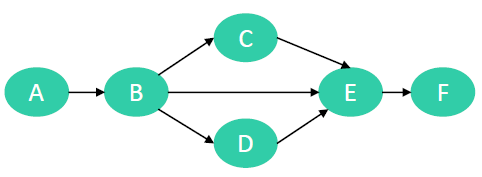
• A 是 B 的前驱活动，B 是 A 的后继活动
• B 是 C 的前驱活动，C 是 B 的后继活动
• …

拓扑排序 - 思路

可以使用卡恩算法（Kahn于1962年提出）完成拓扑排序。

假设 L 是存放拓扑排序结果的列表：

• ① 把所有入度为 0 的顶点放入 L 中，然后把这些顶点从图中去掉
  ② 重复操作 ①，直到找不到入度为 0 的顶点
• 如果此时 L 中的元素个数和顶点总数相同，说明拓扑排序完成
• 如果此时 L 中的元素个数少于顶点总数，说明原图中存在环，无法进行拓扑排序

实现

/**
 * 拓扑排序
 */
@Override
public List<V> topologicalSort() {
	List<V> list = new ArrayList<>();
	Queue<Vertex<V, E>> queue = new LinkedList<>();
	Map<Vertex<V, E>, Integer> ins = new HashMap<>();
	
	// 初始化（将度为0的节点放入队列）
	vertices.forEach((V v, Vertex<V, E> vertex) -> {
		int indegree = vertex.inEdges.size(); // 入度
		if(indegree == 0) { // 入度为0，放入队列
			queue.offer(vertex);
		} else { // 入度不为0，用map记录它的入度
			ins.put(vertex, indegree);
		}
	});	
	
	while(!queue.isEmpty()){ // 从队列中取节点
		Vertex<V, E> vertex = queue.poll();
		list.add(vertex.value); // 放入返回结果中
		
		for (Edge<V, E> edge : vertex.outEdges){
			// 队列中取出节点所通向节点的入度
			int toIndegree = ins.get(edge.to) - 1;
			if(toIndegree == 0) { // 入度为0，放入队列
				queue.offer(edge.to);
			} else { // 入度不为0，用map记录它的入度
				ins.put(edge.to, toIndegree);
			}
		}
	}
	
	return list;
}

生成树

生成树（Spanning Tree），也称为支撑树

• 连通图的极小连通子图，它含有图中全部的 n 个顶点，恰好只有 n – 1 条边

最小生成树（Minimum Spanning Tree）

最小生成树（Minimum Spanning Tree，简称MST）

• 也称为最小权重生成树（Minimum Weight Spanning Tree）、最小支撑树
• 是所有生成树中，总权值最小的那棵
• 适用于有权的连通图（无向）

最小生成树在许多领域都有重要的作用，例如：

• 要在 n 个城市之间铺设光缆，使它们都可以通信
• 铺设光缆的费用很高，且各个城市之间因为距离不同等因素，铺设光缆的费用也不同
• 如何使铺设光缆的总费用最低？—— 最小生成树的应用

如果图的每一条边的权值都互不相同，那么最小生成树将只有一个，否则可能会有多个最小生成树。

求最小生成树的2个经典算法：

• Prim（普里姆算法）
• Kruskal（克鲁斯克尔算法）

Prim算法

切分定理

切分（Cut）

• 把图中的节点分为两部分，称为一个切分。
  下图有个切分 C = (S, T)，S = { A, B, D }，T = { C, E }

横切边（Crossing Edge）

• 如果一个边的两个顶点，分别属于切分的两部分，这个边称为横切边。
  比如上图的边 BC、BE、DE 就是横切边

切分定理：给定任意切分，横切边中权值最小的边必然属于最小生成树。

Prim算法 – 执行过程

假设 G = (V，E) 是有权的连通图（无向），A 是 G 中最小生成树的边集

• 算法从 S = { u0 }（u0 ∈ V），A = { } 开始，重复执行下述操作，直到 S = V 为止
  找到切分 C = (S，V – S) 的最小横切边 (u0，v0) 并入集合 A，同时将 v0 并入集合 S

Prim算法 – 代码实现

Kruskal算法

Kruskal算法 – 执行过程

Kruskal算法 – 代码实现