最小生成树(Minimum Spanning Tree)
生成树(Spanning Tree),也称为支撑树
- 连通图的极小连通子图,它含有图中全部的 n 个顶点,恰好只有 n – 1 条边

最小生成树(Minimum Spanning Tree,简称MST)
- 也称为最小权重生成树(Minimum Weight Spanning Tree)、最小支撑树
- 是所有生成树中,总权值最小的那棵
- 适用于有权的连通图(无向)

最小生成树在许多领域都有重要的作用,例如:
- 要在 n 个城市之间铺设光缆,使它们都可以通信
- 铺设光缆的费用很高,且各个城市之间因为距离不同等因素,铺设光缆的费用也不同
- 如何使铺设光缆的总费用最低?—— 最小生成树的应用
如果图的每一条边的权值都互不相同,那么最小生成树将只有一个,否则可能会有多个最小生成树。
求最小生成树的2个经典算法:
- Prim(普里姆算法)
- Kruskal(克鲁斯克尔算法)
Prim算法
切分定理
切分(Cut)
- 把图中的节点分为两部分,称为一个切分。
下图有个切分 C = (S, T),S = { A, B, D },T = { C, E }
 横切边(Crossing Edge)
横切边(Crossing Edge)
- 如果一个边的两个顶点,分别属于切分的两部分,这个边称为横切边。
比如上图的边 BC、BE、DE 就是横切边
切分定理:给定任意切分,横切边中权值最小的边必然属于最小生成树。
Prim算法 – 执行过程
假设 G = (V,E) 是有权的连通图(无向),A 是 G 中最小生成树的边集
- 算法从 S = { u0 }(u0 ∈ V),A = { } 开始,重复执行下述操作,直到 S = V 为止
找到切分 C = (S,V – S) 的最小横切边 (u0,v0) 并入集合 A,同时将 v0 并入集合 S



Prim算法 – 代码实现
public Set<EdgeInfo<V, E>> mst() {
return prim();
}
private Set<EdgeInfo<V, E>> prim(){
// 最小生成树的顶点数量为: 图的顶点数 1
int verticesSize = vertices.size();
Iterator<Vertex<V, E>> it = vertices.values().iterator(); // map的迭代器
if(!it.hasNext()) return null;
Set<EdgeInfo<V, E>> edgeInfos = new HashSet<>();
Set<Vertex<V, E>> addedVertices = new HashSet<>(); // 标记已经添加的顶点
Vertex<V, E> vertex = it.next(); // 随机取出一个顶点
addedVertices.add(vertex);
MinHeap<Edge<V, E>> heap = new MinHeap<>(vertex.outEdges, edgeComparator);
while(!heap.isEmpty() && addedVertices.size() < verticesSize){
Edge<V, E> edge = heap.remove();
if(addedVertices.contains(edge.to)) continue;
edgeInfos.add(edge.info());
addedVertices.add(edge.to);
heap.addAll(edge.to.outEdges);
}
return edgeInfos;
}
Kruskal算法
Kruskal算法 – 执行过程
按照边的权重顺序(从小到大)将边加入生成树中,直到生成树中含有 V–1 条边为止( V 是顶点数量)
- 若加入该边会与生成树形成环,则不加入该边
- 从第 3 条边开始,可能会与生成树形成环



Kruskal算法 – 代码实现
需要用到并查集数据结构,用来判断加入的边是否会形成环。
public Set<EdgeInfo<V, E>> mst() {
return kruskal();
}
private Set<EdgeInfo<V, E>> kruskal(){
// 最小生成树的顶点数量为: 图的顶点数 1
int edgeSize = vertices.size() - 1;
if(edgeSize == -1) return null; // 空的图
Set<EdgeInfo<V, E>> edgeInfos = new HashSet<>();
MinHeap<Edge<V, E>> heap = new MinHeap<>(edges, edgeComparator);
// 并查集用来判断加入的边是否会形成环
UnionFind<Vertex<V, E>> uf = new UnionFind<>();
// 初始化并查集,将其中每个元素设置为单独的集合
vertices.forEach((V v, Vertex<V, E> vertex) -> {
uf.makeSet(vertex);
});
while(!heap.isEmpty() && edgeInfos.size() < edgeSize){
Edge<V, E> edge = heap.remove();
if(uf.isSame(edge.from, edge.to)) continue;
edgeInfos.add(edge.info());
uf.union(edge.from, edge.to);
}
return edgeInfos;
}
最短路径(Shortest Path)
最短路径是指两顶点之间权值之和最小的路径(有向图、无向图均适用,不能有负权环)
有向图:

无向图:

最短路径的典型应用之一:路径规划问题
求解最短路径的3个经典算法:
- 单源最短路径算法
- Dijkstra(迪杰斯特拉算法)
- Bellman-Ford(贝尔曼-福特算法)
- 多源最短路径算法
- Floyd(弗洛伊德算法)
最短路径 – 概念
无权图
无权图相当于是全部边权值为1的有权图

负权边
有负权边,但没有负权环时,存在最短路径

A到E的最短路径是:A → B → E
负权环
有负权环时,不存在最短路径

通过负权环, A到E的路径可以无限短
A → E → D → F → E → D → F → E → D → F → E → D → F → E → …
Dijkstra
Dijkstra 属于单源最短路径算法,用于计算一个顶点到其他所有顶点的最短路径
- 使用前提:不能有负权边
- 时间复杂度:可优化至 O(ElogV) ,E 是边数量,V 是节点数量
Dijkstra – 等价思考

Dijkstra – 执行过程






Dijkstra – 代码实现版本1(只返回每条最短路径的总权值)
接口文件 Graph.java:
package com.mj.graph;
import java.util.List;
import java.util.Map;
import java.util.Set;
public abstract class Graph<V, E> {
protected WeightManager<E> weightManager; // 权重管理
public Graph() {}
public Graph(WeightManager<E> weightManager) {
this.weightManager = weightManager;
}
public abstract int edgesSize(); // 边的数量
public abstract int verticesSize(); // 顶点数量
public abstract void addVertex(V v); // 添加顶点
public abstract void addEdge(V from, V to); // 添加边
public abstract void addEdge(V from, V to, E weight);// 添加边
public abstract void removeVertex(V v); // 删除顶点
public abstract void removeEdge(V from, V to); // 删除边
public abstract void bfs(V begin, VertexVisitor<V> visitor); // 广度优先搜索
public abstract void dfs(V begin, VertexVisitor<V> visitor); // 深度优先搜索
public abstract List<V> topologicalSort(); // 拓扑排序
public abstract Set<EdgeInfo<V, E>> mst(); // 最小生成树
public abstract Map<V, E> shortestPath(V begin); // 最短路径
public interface WeightManager<E> { // 管理权重
int compare(E w1, E w2); // 比较权重
E add(E w1, E w2); // 权重相加
E zero();
}
public interface VertexVisitor<V>{
boolean visit(V v);
}
public static class EdgeInfo<V, E>{
private V from;
private V to;
private E weight;
public EdgeInfo(V from, V to, E weight) { // 边信息
super();
this.from = from;
this.to = to;
this.weight = weight;
}
public V getFrom() {
return from;
}
public void setFrom(V from) {
this.from = from;
}
public V getTo() {
return to;
}
public void setTo(V to) {
this.to = to;
}
public E getWeight() {
return weight;
}
public void setWeight(E weight) {
this.weight = weight;
}
@Override
public String toString() {
return "EdgeInfo [from=" + from + ", to=" + to + ", weight=" + weight + "]";
}
}
}
@Override
public Map<V, E> shortestPath(V begin) {
Vertex<V, E> beginVertex = vertices.get(begin); // 源点
if(beginVertex == null) return null;
Map<V, E> selectedPaths = new HashMap<>(); // 最终的最短路径
Map<Vertex<V, E>, E> paths = new HashMap<>(); // 当前最短路径
// 初始化paths
for(Edge<V, E> edge : beginVertex.outEdges){
paths.put(edge.to, edge.weight);
}
while(!paths.isEmpty()){
Entry<Vertex<V, E>, E> minEntry = getMinPath(paths); // 挑选出当前最短路径中最短的点
// minVertex 离开桌面,被确定为最终的最短路径
Vertex<V, E> minVertex = minEntry.getKey();
selectedPaths.put(minVertex.value, minEntry.getValue());
paths.remove(minVertex);
// 对它的minVertex的outEdges进行松弛操作
for(Edge<V, E> edge : minVertex.outEdges){
// 如果edge.to已经离开桌面,就没必要进行松弛操作
if(selectedPaths.containsKey(edge.to.value) || edge.to.equals(beginVertex)) continue;
// 新的可选择的最短路径:beginVertex到edge.from的最短路径 + edge.weight
E newWeight = weightManager.add(minEntry.getValue(), edge.weight);
// 以前的最短路径:beginVertex到edge.to的最短路径
E oldWeight = paths.get(edge.to);
if(oldWeight == null || weightManager.compare(newWeight, oldWeight) < 0) {
paths.put(edge.to, newWeight);
}
}
}
return selectedPaths;
}
/**
* 从paths中挑一个最小的路径出来
*/
private Entry<Vertex<V, E>, E> getMinPath(Map<Vertex<V, E>, E> paths) {
Iterator<Entry<Vertex<V, E>, E>> it = paths.entrySet().iterator();
Entry<Vertex<V, E>, E> minEntry = it.next();
while (it.hasNext()) {
Entry<Vertex<V, E>, E> entry = it.next();
if (weightManager.compare(entry.getValue(), minEntry.getValue()) < 0) {
minEntry = entry;
}
}
return minEntry;
}
Dijkstra – 代码实现版本2(返回最短路径的总权值和边信息)
接口文件 Graph.java
接口文件 Graph.java:修改了 shortestPath方法接口,增加了 PathInfo 内部类。
package com.mj.graph;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Set;
public abstract class Graph<V, E> {
protected WeightManager<E> weightManager; // 权重管理
public Graph() {}
public Graph(WeightManager<E> weightManager) {
this.weightManager = weightManager;
}
public abstract int edgesSize(); // 边的数量
public abstract int verticesSize(); // 顶点数量
public abstract void addVertex(V v); // 添加顶点
public abstract void addEdge(V from, V to); // 添加边
public abstract void addEdge(V from, V to, E weight);// 添加边
public abstract void removeVertex(V v); // 删除顶点
public abstract void removeEdge(V from, V to); // 删除边
public abstract void bfs(V begin, VertexVisitor<V> visitor); // 广度优先搜索
public abstract void dfs(V begin, VertexVisitor<V> visitor); // 深度优先搜索
public abstract List<V> topologicalSort(); // 拓扑排序
public abstract Set<EdgeInfo<V, E>> mst(); // 最小生成树
// public abstract Map<V, E> shortestPath(V begin); // 返回总权值的单源最短路径
// 返回路径信息的单源最短路径(dijkstra、bellmanFord)
public abstract Map<V, PathInfo<V, E>> shortestPath(V begin);
// 返回路径信息的多源最短路径(Floyd)
public abstract Map<V, Map<V, PathInfo<V, E>>> shortestPath();
public interface WeightManager<E> { // 管理权重
int compare(E w1, E w2); // 比较权重
E add(E w1, E w2); // 权重相加
E zero();
}
public interface VertexVisitor<V>{
boolean visit(V v);
}
/**
* 最短路径返回的路径信息, 包含到某个顶点的路径信息和总权值
*/
public static class PathInfo<V, E> {
protected E weight; // 权值
protected List<EdgeInfo<V, E>> edgeInfos = new LinkedList<>();
public PathInfo() {}
public PathInfo(E weight) {
this.weight = weight;
}
public E getWeight() {
return weight;
}
public void setWeight(E weight) {
this.weight = weight;
}
public List<EdgeInfo<V, E>> getEdgeInfos() {
return edgeInfos;
}
public void setEdgeInfos(List<EdgeInfo<V, E>> edgeInfos) {
this.edgeInfos = edgeInfos;
}
@Override
public String toString() {
return "PathInfo [weight=" + weight + ", edgeInfos=" + edgeInfos + "]";
}
}
public static class EdgeInfo<V, E>{
private V from;
private V to;
private E weight;
public EdgeInfo(V from, V to, E weight) { // 边信息
super();
this.from = from;
this.to = to;
this.weight = weight;
}
public V getFrom() {
return from;
}
public void setFrom(V from) {
this.from = from;
}
public V getTo() {
return to;
}
public void setTo(V to) {
this.to = to;
}
public E getWeight() {
return weight;
}
public void setWeight(E weight) {
this.weight = weight;
}
@Override
public String toString() {
return "EdgeInfo [from=" + from + ", to=" + to + ", weight=" + weight + "]";
}
}
}
dijkstra 实现1
@Override
public Map<V, PathInfo<V, E>> shortestPath(V begin) {
return dijkstra(begin);
}
private Map<V, PathInfo<V, E>> dijkstra(V begin) {
Vertex<V, E> beginVertex = vertices.get(begin);
if(beginVertex == null) return null;
Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>(); // 最终的最短路径
Map<Vertex<V, E>, PathInfo<V, E>> paths = new HashMap<>(); // 当前的最短路径
// 初始化paths
for (Edge<V, E> edge : beginVertex.outEdges) {
PathInfo<V, E> path = new PathInfo<>();
path.weight = edge.weight;
path.edgeInfos.add(edge.info());
paths.put(edge.to, path);
}
while(!paths.isEmpty()) {
// 挑选出当前最短路径中最短的点
Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = getMinPath(paths);
// minVertex 离开桌面,被确定为最终的最短路径
Vertex<V, E> minVertex = minEntry.getKey();
selectedPaths.put(minVertex.value, minEntry.getValue()); // 放入最终的最短路径
paths.remove(minVertex); // 从当前的最短路径中移除
// 对离开桌面的minVertex的outEdges进行松弛操作
for (Edge<V, E> edge : minVertex.outEdges) {
// 如果edge.to已经离开桌面, 就没有必要进行松弛操作
if(selectedPaths.containsKey(edge.to.value)) continue;
// 新的可选择的最短路径: beginVertex到edge.from的最短路径 + edge.weight
E newWeight = weightManager.add(minEntry.getValue().weight, edge.weight);
// 以前的最短路径: beginVertex到edge.to的最短路径
PathInfo<V, E> oldPath = paths.get(edge.to);
if(oldPath == null || weightManager.compare(newWeight, oldPath.weight) < 0) {
PathInfo<V, E> path = new PathInfo<>();
path.weight = newWeight;
path.edgeInfos.addAll(minEntry.getValue().edgeInfos);
path.edgeInfos.add(edge.info());
paths.put(edge.to, path);
}
}
}
selectedPaths.remove(begin);
return selectedPaths;
}
/**
* 从paths中挑一个最小的路径出来(遍历)
* 可用小顶堆进行优化
*/
private Entry<Vertex<V, E>, PathInfo<V, E>> getMinPath(Map<Vertex<V, E>, PathInfo<V, E>> paths) {
Iterator<Entry<Vertex<V, E>, PathInfo<V, E>>> it = paths.entrySet().iterator();
Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = it.next();
while (it.hasNext()) {
Entry<Vertex<V, E>, PathInfo<V, E>> entry = it.next();
if (weightManager.compare(entry.getValue().weight, minEntry.getValue().weight) < 0) {
minEntry = entry;
}
}
return minEntry;
}
dijkstra 实现2(封装了relax松弛操作)
private Map<V, PathInfo<V, E>> dijkstra(V begin) {
Vertex<V, E> beginVertex = vertices.get(begin);
if(beginVertex == null) return null;
Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>(); // 最终的最短路径
Map<Vertex<V, E>, PathInfo<V, E>> paths = new HashMap<>(); // 当前的最短路径
paths.put(beginVertex, new PathInfo<>(weightManager.zero()));
// 初始化paths
// for (Edge<V, E> edge : beginVertex.outEdges) { // 遍历源点出去的边, 添加到当前的最短路径中
// PathInfo<V, E> path = new PathInfo<>();
// path.weight = edge.weight;
// path.edgeInfos.add(edge.info());
// paths.put(edge.to, path);
// }
while(!paths.isEmpty()) {
// 挑选出当前最短路径中最短的点
Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = getMinPath(paths);
// minVertex 离开桌面,被确定为最终的最短路径
Vertex<V, E> minVertex = minEntry.getKey();
PathInfo<V, E> minPath = minEntry.getValue();
selectedPaths.put(minVertex.value, minPath); // 放入最终的最短路径
paths.remove(minVertex); // 从当前的最短路径中移除
// 对离开桌面的minVertex的outEdges进行松弛操作
for (Edge<V, E> edge : minVertex.outEdges) {
// 如果edge.to已经离开桌面, 就没有必要进行松弛操作
if(selectedPaths.containsKey(edge.to.value)) continue;
relaxForDijkstra(edge, minPath, paths);
}
}
selectedPaths.remove(begin);
return selectedPaths;
}
/**
* 松弛
* @param edge 需要进行松弛的边
* @param fromPath edge的from的最短路径信息
* @param paths 存放着其他(对于dijkstra来说, 就是还没有离开桌面的点)的最短路径信息
*/
private void relaxForDijkstra(Edge<V, E> edge, PathInfo<V, E> fromPath, Map<Vertex<V, E>, PathInfo<V, E>> paths) {
// 新的可选择的最短路径: beginVertex到edge.from的最短路径 + edge.weight
E newWeight = weightManager.add(fromPath.weight, edge.weight);
// 以前的最短路径: beginVertex到edge.to的最短路径
PathInfo<V, E> oldPath = paths.get(edge.to);
if(oldPath != null && weightManager.compare(newWeight, oldPath.weight) >= 0) return;
if(oldPath == null) { // 新创建的边
oldPath = new PathInfo<>();
paths.put(edge.to, oldPath);
} else { // 以前就存在的边
oldPath.edgeInfos.clear();
}
oldPath.weight = newWeight;
oldPath.edgeInfos.addAll(fromPath.edgeInfos);
oldPath.edgeInfos.add(edge.info());
}
/**
* 从paths中挑一个最小的路径出来(遍历)
* 可用小顶堆进行优化
*/
private Entry<Vertex<V, E>, PathInfo<V, E>> getMinPath(Map<Vertex<V, E>, PathInfo<V, E>> paths) {
Iterator<Entry<Vertex<V, E>, PathInfo<V, E>>> it = paths.entrySet().iterator();
Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = it.next();
while (it.hasNext()) {
Entry<Vertex<V, E>, PathInfo<V, E>> entry = it.next();
if (weightManager.compare(entry.getValue().weight, minEntry.getValue().weight) < 0) {
minEntry = entry;
}
}
return minEntry;
}
dijkstra 测试
运行:


Bellman-Ford
Bellman-Ford 也属于单源最短路径算法,支持负权边,还能检测出是否有负权环
- 算法原理:对所有的边进行 V – 1 次松弛操作( V 是节点数量),得到所有可能的最短路径
- 时间复杂度:O(EV) ,E 是边数量,V 是节点数量
下图的最好情况是恰好从左到右的顺序对边进行松弛操作:
- 对所有边仅需进行 1 次松弛操作就能计算出A到达其他所有顶点的最短路径

最坏情况是恰好每次都从右到左的顺序对边进行松弛操作:
- 对所有边需进行 V – 1 次松弛操作才能计算出A到达其他所有顶点的最短路径

Bellman-Ford – 实例



Bellman-Ford – 代码实现
@Override
public Map<V, PathInfo<V, E>> shortestPath(V begin) {
// return dijkstra(begin);
return bellmanFord(begin);
}
private Map<V, PathInfo<V, E>> bellmanFord(V begin) {
Vertex<V, E> beginVertex = vertices.get(begin); // 源点
if(beginVertex == null) return null;
// 存放当前最短路径信息(不断的进行松弛操作, 会变成最终的最短路径)
Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>();
// 初始化源点的最短路径信息
selectedPaths.put(begin, new PathInfo<>(weightManager.zero()));
int count = vertices.size() - 1; // 进行 V -1 次松弛操作, 必然能找到最短路径
for (int i = 0; i < count; i++) {
for (Edge<V, E> edge : edges) { // 对所有边进行松弛操作
// 获取该边的始点的最短路径信息, 用于后面进行松弛操作
PathInfo<V, E> fromPath = selectedPaths.get(edge.from.value);
// 如果该点的始点没有最短路径信息,松弛必然失败,直接进入下一轮
if(fromPath == null) continue;
relax(edge, fromPath, selectedPaths); // 松弛操作
}
}
// 检测负权环, 前面已经松弛了V-1次,这里如果松弛第 V 次仍然可以成功, 说明有负权环
for (Edge<V, E> edge : edges) {
PathInfo<V, E> fromPath = selectedPaths.get(edge.from.value);
if(fromPath == null) continue;
if(relax(edge, fromPath, selectedPaths)) {
System.out.println("有负权环, 不存在最短路径");
return null;
}
}
selectedPaths.remove(begin); // 从最短路径中移除源点的最短路径信息
return selectedPaths;
}
/**
* 松弛
* @param edge 需要进行松弛的边
* @param fromPath edge的from的最短路径信息
* @param paths 存放着其他的最短路径信息
*/
private boolean relax(Edge<V, E> edge, PathInfo<V, E> fromPath, Map<V, PathInfo<V, E>> paths) {
// 新的可选择的最短路径: beginVertex到edge.from的最短路径 + edge.weight
E newWeight = weightManager.add(fromPath.weight, edge.weight);
// 以前的最短路径: beginVertex到edge.to的最短路径
PathInfo<V, E> oldPath = paths.get(edge.to.value);
if(oldPath != null && weightManager.compare(newWeight, oldPath.weight) >= 0) return false;
if(oldPath == null) { // 新创建的边
oldPath = new PathInfo<>();
paths.put(edge.to.value, oldPath);
} else { // 以前就存在的边
oldPath.edgeInfos.clear();
}
oldPath.weight = newWeight;
oldPath.edgeInfos.addAll(fromPath.edgeInfos);
oldPath.edgeInfos.add(edge.info());
return true;
}
/**
* 从paths中挑一个最小的路径出来(遍历)
* 可用小顶堆进行优化
*/
private Entry<Vertex<V, E>, PathInfo<V, E>> getMinPath(Map<Vertex<V, E>, PathInfo<V, E>> paths) {
Iterator<Entry<Vertex<V, E>, PathInfo<V, E>>> it = paths.entrySet().iterator();
Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = it.next();
while (it.hasNext()) {
Entry<Vertex<V, E>, PathInfo<V, E>> entry = it.next();
if (weightManager.compare(entry.getValue().weight, minEntry.getValue().weight) < 0) {
minEntry = entry;
}
}
return minEntry;
}
测试


Floyd
Floyd 属于多源最短路径算法,能够求出任意2个顶点之间的最短路径,支持负权边
- 时间复杂度:O(V3),效率比执行 V 次 Dijkstra 算法要好( V 是顶点数量)
注:单源最短路径算法对每个顶点求一次,同样可以求出任意2个顶点之间的最短路径
算法原理:
- 从任意顶点
i到任意顶点j的最短路径不外乎两种可能
① 直接从i到j
② 从i经过若干个顶点到j - 假设
dist(i, j)为顶点i到顶点j的最短路径的距离 - 对于每一个顶点
k,检查dist(i, k)+dist(k, j)<dist(i, j)是否成立
如果成立,证明从i到k再到j的路径比i直接到j的路径短,
设置dist(i, j)=dist(i, k)+dist(k, j); - 当我们遍历完所有结点
k,dist(i, j)中记录的便是i到j的最短路径的距离
算法原理伪代码:
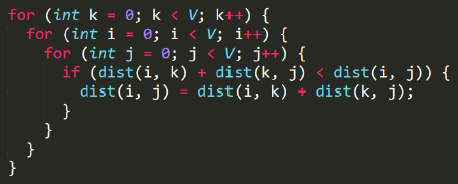
Floyd – 代码实现
接口文件中:
public abstract Map<V, Map<V, PathInfo<V, E>>> shortestPath(); // 多源最短路径
/**
* 多源最短路径: Floyd
*/
@Override
public Map<V, Map<V, PathInfo<V, E>>> shortestPath() {
// 最终的返回值, 存放着每个顶点, 以及每个顶点到其他顶点的最短路径
Map<V, Map<V, PathInfo<V, E>>> paths = new HashMap<>();
// 初始化: 遍历所有顶点, 初始化每个顶点到它的出去的点的最短路径信息
for (Edge<V, E> edge : edges) {
// 取出当前边的最短路径信息, 为空则创建一个并赋值
Map<V, PathInfo<V, E>> map = paths.get(edge.from.value);
if (map == null) {
map = new HashMap<>();
paths.put(edge.from.value, map);
}
PathInfo<V, E> pathInfo = new PathInfo<>(edge.weight);
pathInfo.edgeInfos.add(edge.info());
map.put(edge.to.value, pathInfo);
}
vertices.forEach((V v2, Vertex<V, E> vertex2) -> {
vertices.forEach((V v1, Vertex<V, E> vertex1) -> {
vertices.forEach((V v3, Vertex<V, E> vertex3) -> {
if (v1.equals(v2) || v2.equals(v3) || v1.equals(v3)) return;
// v1 -> v2
PathInfo<V, E> path12 = getPathInfo(v1, v2, paths);
if (path12 == null) return;
// v2 -> v3
PathInfo<V, E> path23 = getPathInfo(v2, v3, paths);
if (path23 == null) return;
// v1 -> v3
PathInfo<V, E> path13 = getPathInfo(v1, v3, paths);
E newWeight = weightManager.add(path12.weight, path23.weight);
if (path13 != null && weightManager.compare(newWeight, path13.weight) >= 0) return;
if (path13 == null) {
path13 = new PathInfo<>();
paths.get(v1).put(v3, path13); // v1 到 v3的最短路径
} else {
path13.edgeInfos.clear();
}
// 将v1到v3的路径信息更新为, v1到v2再到v3
path13.weight = newWeight;
path13.edgeInfos.addAll(path12.edgeInfos);
path13.edgeInfos.addAll(path23.edgeInfos);
});
});
});
return paths;
}
private PathInfo<V, E> getPathInfo(V from, V to, Map<V, Map<V, PathInfo<V, E>>> paths) {
Map<V, PathInfo<V, E>> map = paths.get(from);
return map == null ? null : map.get(to);
}
Floyd — 测试


