LCA问题:给定一颗 \(n\) 个结点的有根树,有 \(m\) 次询问,每次询问给出结点 \(a,b\) ,求 \(a,b\) 的最近公共祖先。此类问题通称 LCA 。
暴力
一次一次把 \(a,b\) 向上提,知道 \(a\) 与 \(b\) 相等为止。
倍增加速
在上面暴力的思想中,是一步一步向上跳的。
倍增的核心思想就是 \(2^j\) 步 \(2^j\) 步向上跳。
我们需要先处理出第 \(i\) 个点的第 \(2^j\) 个祖先。
如何求出?
设 \(f_{i,j}\) 为第 \(i\) 个点向上跳 \(2^j\) 后所处的位置,根据初一学习的幂的性质,我们认为第 \(i\) 个点向上跳 \(2^j\) 后所处的位置就是第 \(i\) 个点向上跳 \(2^{j-1}\) 后再向上跳 \(2^{j-1}\) (\(2^{j-1}+2^{j-1}=2^j\))。
所以我们有:
可以递推出来:
void dfs(int u, int fa) //当前是第 u 个结点,u 的父亲是 fa
{
d[u] = d[fa]+1; /顺便计算深度
for(int i=1; (1<<i) <= d[u]; i++) //(1<<i)就是 2^i ,枚举2的次幂不能超过当前结点的深度
f[u][i] = f[ f[u][i-1] ][i-1];
for(int i=head[u]; i; i=nxt[i])
{
int v = ver[i];
if(v == fa) continue;
f[v][0] = u;
dfs(v, u);
}
}
我们有了 \(f\) ,可以干啥呢?
假设要求 \(\text{LCA}(a,b)\) :
我们需要先把 \(a,b\) 弄成同一深度,方便待会“一起跳”。
那么为了把 \(a,b\) 弄成同一深度,显然需要把那个深度更深的结点不断向上跳,直到深度等于另一个结点为止。
为了避免麻烦,我们先让 \(a\) 变成那个深度更大的结点即可。不影响最终结果。
我们有代码:
if(d[a]<d[b]) swap(a, b);
for(int i=20; i>=0; i--) //2^20足够了。想要省事可以用 log(a) 优化
{
if(d[f[a][i]] >= d[b]) a = f[a][i];
//把 a 不断向上跳
if(a == b) return a;
//特判。如果两个点相等那么 LCA(a, b) 就是深度小的那个点
}
我们考虑从一个较大的数 \(i\) 作为 \(2\) 的次幂枚举,如果 \(a,b\) 两点的第 \(2^i\) 个祖先(即 \(f_{a,i}\ \text{和}\ f_{b,i}\) )不一样,那么就
也就是 \(a,b\) 同时向上跳 \(2^i\) 步。
这样,在从大到小枚举所有的 \(i\) 之后,当前的 \(a',b'\) 必定是 \(\text{LCA}(a,b)\) 的左右儿子,那么返回一个 \(f_{a',0}\text{或}f_{b',0}\) 即可(即 \(a',b'\) 的父亲)。
注意!这里说的都是从大到小枚举 \(2\) 的次幂,一定要记住,否则这个算法就错了。
我们有求 \(\text{LCA}(a,b)\) 的代码:
int LCA(int a, int b)
{
if(d[a]<d[b]) swap(a, b);
for(int i=20; i>=0; i--)
{
if(d[f[a][i]] >= d[b]) a = f[a][i];
if(a == b) return a;
}
for(int i=20; i>=0; i--)
if(f[a][i] != f[b][i])
a = f[a][i], b = f[b][i];
return f[a][0];
//此处亦可返回 f[b][0] ,答案都一样
}
是不是很简单呢。
考虑为什么倍增 LCA 不会超时。
就像上面说的一样,暴力做法是一步一步往上跳,相当于每次只跳 \(2^0\) 步。
而倍增 LCA 通过从大到小枚举 \(2\) 的次幂,在枚举到每个 \(i\) 时一下会跳 \(2^i\) 次,在倍增中只跳了一次,而在暴力中要跳 \(2^i\) 次!差异可想而知。
接下来谈谈为什么从 \(i=20\) 开始枚举。
如果您多尝试几次,就会发现其实一般数据根本不会用到 \(i=17\) 之前的值!
为什么呢?看下面:
来观察 \(y=2^x\) 的函数图像:
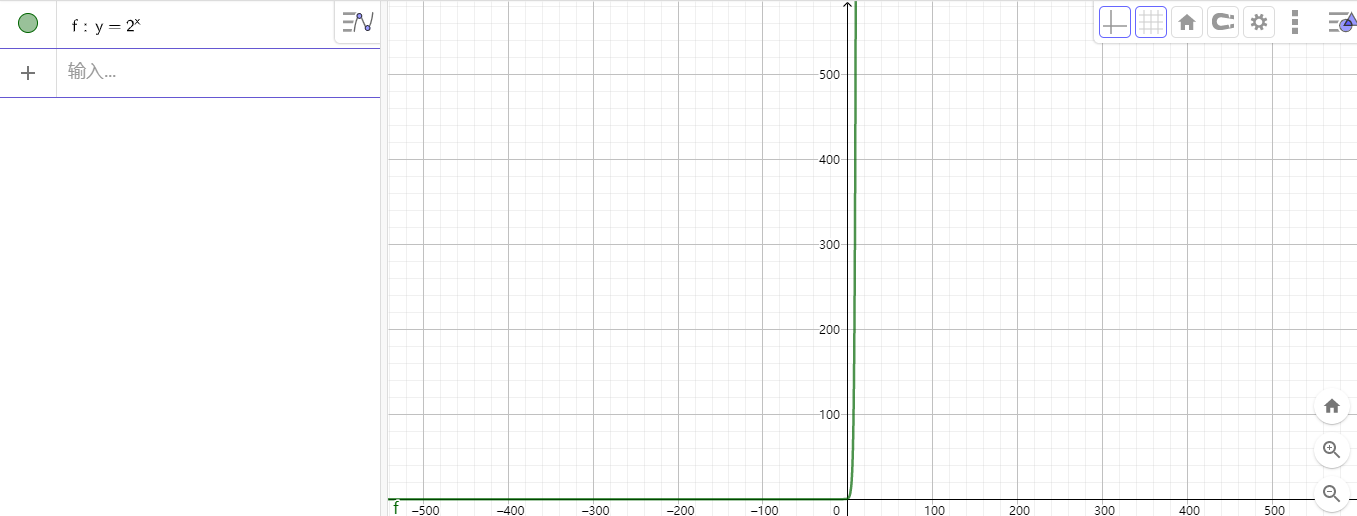
发现了什么?函数 \(y=2^x\) 的增长速度是指数级的!
那么为什么说数据根本不会用到 \(i=17\) 之前的值呢?
而在洛谷的 LCA 模板题中,点数 \(n\) 的最大值才为 \(5\times 10^5\)!
一般来说,我们可以让 \(i\) 从 \(\log\ a\) 开始枚举。这样会更有效。
顺带一提,由于我们求出 \(f\) 数组需要耗费 \(\mathcal{O}(\log\ n)\) 的复杂度,而真正求 LCA 只需要 \(\mathcal{O}(1)\) 的时间复杂度,故单次查询时间复杂度为 \(\mathcal{O}(\log\ n)\) 。
考虑为什么倍增 LCA 的正确性。
在倍增 LCA 的算法中,我们发现对于 \(a,b\) 必须满足一个条件:可以拆成任意个 \(2\) 的次幂相加的形式,否则就无法倍增的跳到答案的左、右儿子。
例如说:
故对于编号为 \(11\) 的点一条可行的路径为:
由于百度的原因,我们知道了任意一个正整数都可以拆分成 \(2\) 的次幂的形式。故倍增 LCA 是必定正确的。
考虑为什么从大到小枚举 \(2\) 的次幂。
其实很简单。如果从小到大枚举,那么几乎小于 \(x\) (所要求 LCA 的一个值)的任意一个 \(2\) 的次幂都会计入答案。那么是不是就意味着会出现“跳不到答案的左右儿子”这个情况(因为你先跳小的,那么有可能到某个节点(不是答案结点的左右儿子)时 \(2\) 的越来越大的次幂就无法跳了)。
为了避免这种情况,我们就需要从大向小枚举。这样,不能跳的也不会跳。仔细想一想似乎也很符合倍增 LCA 的思想:一次跳很多步。