之前第5节课留了个疑问,是关于“时间t被安排进R”的时间复杂度能不能为Ο(log2n)?”和BST时间复杂度Ο(h)的关系。第6节对此继续了深入的探讨。首先我们知道BST的h是指树的高,即从根到叶子结点最长路径的长度。但由于树结构不同平衡情况,高h的结果也不一样,如下图所示:

一、结点的高
由此可以看出,平衡树结构下的高h具有计算性。那么接下来我们再看下各结点的高(height of node)的计算方式,它是从该节点位置下到最底部的叶子节点的最长路径长度 (height of node = max(左子树高,右子树高) + 1):

二、AVL
我们如果想让Ο(h)=Ο(log2n),就必须把BST变为平衡树,但现实中,不一定所有数列都能构成完全的平衡树,但可以构成高度平衡树AVL(由Adelson-Velsky和E.M. Landis发明的),在该树下,每个结点的左右子树相差最多±1。如下图所示:
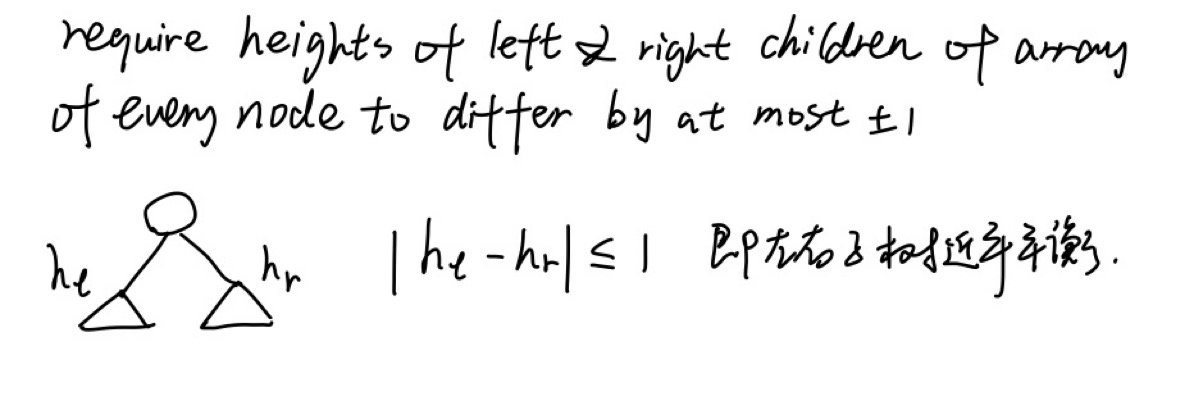
但有时会出现很糟糕的情况:右子树高比左子树高多1.

假设AVL节点数量为Nh,那么由上图,可得Nh = n = 1 + Nh-1 + Nh-2。这个如果算下去(课程没给出具体过程),会得到Nh > Fh = φh/√5,其中Fh是斐波那契数列(数字1,1,2,3,5,8-构成了一个序列。这个数列前面相邻两项之和,构成了后一项),φ=1.618,最后可以通过下图的得到h小于1.44log2n。
除了通过上述方法,还有种更简单的方法估算h的大小:
在该方法下得到的结果2log2n不如1.44log2n来的更为准确。
三、AVL的插入
AVL的插入分两步走:
- 简单的二分搜索树BST插入(simple BST insert);
- 从修改结点向上满足AVL属性,因为下面插入可能会影响上面的结果(Fix AVL property from changed node up)。
举个例子可能会更好的解释上面的步骤:
(注:蓝色箭头表明哪边子树比较重。)
上图我们给定了一个BST,然后按照BST插入的方法将23插入进去,我们会发现,29-26-23不符合AVL的属性。为了解决这个问题,AVL有个旋转Rotiation操作,如下图:
如果我们对29-26-23进行右旋转即可得到正确的AVL结构:
除了上面这种情况,如果出现下图这种插入55后的情况,可以使用双旋转操作(double/two rotation):
那么现在我们来假设一个通用场景,总结下AVL的调整方法。
假设x是最低违背AVL的结点,然后right(x)(或x.right)更高。出现下面两种情况则可以参考下面的旋转方案:
四、AVL排序
- 插入n个items - 每插入一个item要花费h时间,h在平衡树下为log2n,因此n个items为Ο(nlog2n) ;
- in-order traversal 按顺序遍历输出 - Ο(n) 。
五、总结
对于插入、删除、最小化,使用Heap和AVL就可以了,但是如果要求next_larger和next_smaller得要平衡二分查找树,不过现实很难满足完全平衡,那么用AVL高度平衡树来做也行。