关于网络流
网络最大流,简称网络流,是一种流量问题。
用数学语言就是如下表示:
给定原图 \(G=(E,V)\),要求出 \(G'=(E',V')\),满足:
- \(V'=V\),即两图点集相同。
- \(\forall e\in E,\exists e'\in E'\ e_d=e'_d,e_s=e'_s,e_v\ge e'_v\),即两图的结构相同,且 \(G'\) 里的边权不大于 \(G\) 里的对应边的边权。
- \(\exists s,t\in V \ \sum\limits_{e\in E'\\ e_t=s}e_v=0,\sum\limits_{e\in E'\\e_s=t}e_v=0\),即新图存在一个源点 \(s\),和一个汇点 \(t\),使得 \(s\) 入度为 \(0\),\(t\) 出度为 \(0\)。
- \(\forall v\in V,v\neq s,v\neq t\ \sum\limits_{e\in E'\\e_s=v}e_v=\sum\limits_{e\in E'\\e_t=v}e_v\),即对于所有非源点、汇点的点,带权入度与带权出度相等。
求出 \(\max \sum\limits_{e\in E'\\e_d=t}e_v\)。
用通俗语言讲,就是一个水系统,在注满了水以后,从源点到汇点的最大流水量。
如何求解网络流
有两种主流方法:
- 增广路算法。指不断寻找能够增加流量的路径来求解。
- 预流推进算法。指通过模拟水流的推动过程来求解。
一般来说,增广路算法有 EK,Dinic 和 ISAP。而预留推进算法有 HLPP 算法。
在求解最短路时,通常采用 ISAP 或 HLPP 算法。但是 HLPP 算法常数较大,一般情况下都使用 ISAP 算法求解网络最大流。
关于增广路算法
关于增广路算法,有一下几个定义:
反向边 \(\&\) 残余网络
定义 \(e'\) 为 \(e\) 的反向边,当且仅当 \(e'_s=e_t\),\(e'_t=e_s\),\(e'_v\) 为 \(e\) 已经使用的流量。
反向边的意义为执行贪心算法时,用于“反悔”。即就算选择了错误的增广路,也可以通过走反向边纠正。
定义原图和原图每一条边的反向边的并集为原图的残余网络。
增广路
定义一条从源点到汇点的路径为最短路,当且仅当这条路径上每一条边的剩余流量不为零。
增广路算法的基本逻辑
即以下流程:
- 寻找一条或几条增广路,若找不到,退出算法;
- 将增广路上能增加的流量增加到整体流量上;
- 返回第一步。
何为 ISAP 算法?
ISAP (Improved Shortest Augment Path) 是 SAP 算法的优化。融合了 SAP 和 Dinic 的思想。是增广路算法中平均速度最快的算法。
ISAP 在基本的增广路算法流程上,优化了寻找增广路的方法。
基本操作如下:
- 进行一次从汇点到源点的反向宽搜,对原图分层。
- 从源点开始进行若干次深搜。深搜出来增广路,再将增广路上的节点层数 \(+1\)。
接下来我们想一想,为什么这样是正确的,以及为什么这么做效率高。
注:下面的图片,若未注明,则编号最小的节点为源点,编号最大的节点为汇点。
首先,你要找增广路。怎么去找呢?
妈妈,我会 DFS!
很好,于是你就去 DFS 找增广路了。
顺带一提,这样的算法称作 Ford-Fulkerson 算法
直到有一天,你看到了这样一张图:
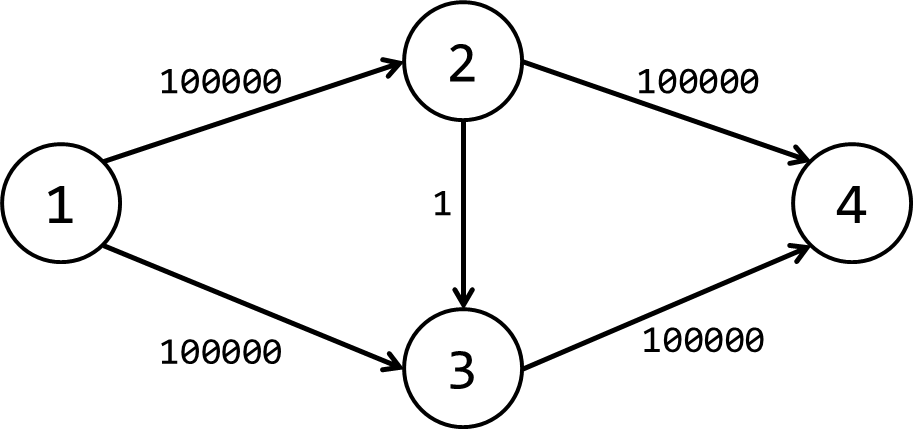
不知道什么奇怪的原因,你搜到了 \(1\rightarrow 2\rightarrow 3\rightarrow 4\) 这条路径。
接下来,你又搜了 \(1\rightarrow 3\rightarrow 2\rightarrow 4\)。
然后……(又经过了 \(199998\) 步后)……你终于搜完了。
看起来没毛病……然而出题人看着很不爽。
过了一天,出题人加强了数据。现在,这条边变得更粗♂了:
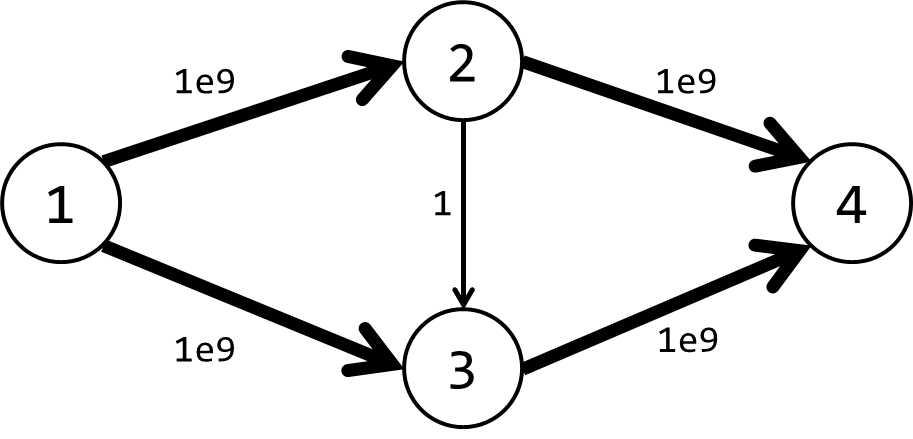
真·硬核变粗
结果,你的算法依旧出现了那个问题……出题人看你不爽,丢了一个 TLE 给你。
Ford-Fulkerson:卒。
完了,这下该怎么办呢?
妈妈,我会 BFS!
女少口阿!利用 BFS 总是能够搜出最短路的 特性,我们就能够完美解决这个问题。
这个算法叫做 Edmonds-Karp,或者是 SAP。
就在你洋洋得意之时,出题人读透了你的心思,便给你丢了这么一张图:
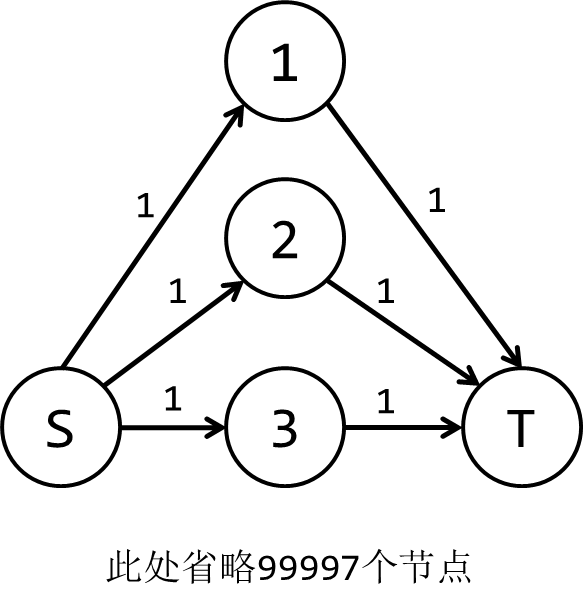
你的算法成功被卡到了 \(\mathcal{O}(n^2)\),TLE。
Edmonds-Karp:卒。
此时,你的内心应该是崩溃的。
啊啊啊,DFS 不行,BFS 不行,还能怎么办啊?
难不成……要结合起来?
Bingo!加一分。
没错,我们确实要让 DFS 与 BFS 结合起来。那么,怎么结合呢?
我们先来比较 DFS 与 BFS 的好坏:
| DFS | BFS | |
|---|---|---|
| 优点 | 占用空间少,速度快 | 可以搜出最短增广路 |
| 缺点 | 可能因为增广路过长而导致重复 | 有时会被卡到全图遍历 |
我们经过反复考量后,打算改造 DFS。
为什么?因为 BFS 的结构导致一定会被卡到全图遍历。除非变成 A* 才能有优化。
(额我是不是一不小心说漏了什么)
那么,我们怎样才能让 DFS 跑的是最短增广路呢?我们考虑给图分层。
每一次 BFS 都将这张图分层。接下来 DFS 只会在相邻两层之间跑来跑去。
当两个节点之间没有剩余流量时,就视为不连通。
这样,我们就能既有最短路,又能够避免全图遍历了。
恭喜你,你已经想到了 Dinic 算法。Dinic 的核心就是上面的流程。
当然,Dinic 还有很多细节上的优化,这个我们待会儿再讲。
当然,某些毒瘤出题人看 Dinic 不爽,打算来卡一卡。
这样的数据是有的,而且有的是。
卡 Dinic 的核心就是让它不停地跑 BFS,导致整体复杂度趋近上限 \(\mathcal{O}(n^2m)\)。
所以,我们还需要一个究极算法,来拯救被毒瘤出题人蹂躏的 Dinic。
就在这时,ISAP 横空出世,成功教那些出题人做人。
ISAP 的核心优化就是将那个可恶的反复 BFS 干掉了,变成了只做一次 BFS 的事情。
问题是,如何在只有一次 BFS 的情况下完成分层,并且一直维护这个分层呢?
之前 Dinic 要一直跑 BFS 的原因是 DFS 无法维护。这个分层是连通与否的分层。
ISAP 的分层则是在每一次找到一条增广路后,提高每一个点的层数。
这样,就能依次走最短路,次短路,等等。就可以不用多次跑 BFS 了。
出题人听到了这句话以后很开心,因为下面这张图你跑不过:

???为什么跑不过啊,因为你一次 DFS 只能找一条最短增广路。但是,最短增广路完全有可能不止一条。
那么,我能不能在一次 DFS 中找到很多条最短增广路,以至于形成了一个增广路网呢?
Bingo!再加一分。
这样,你就成功解锁了基本版 ISAP。(当然,对于每一个增广路网上的节点,高度只需要增加 \(1\))
问题是,出题人发现你的 ISAP 很弱,于是就来疯狂卡你。你不得不通过寻找优化来跟进速度。
首先,如果你的 DFS 在某一个节点上没有跑满,也就是说还有节点可以往外灌,那么你这个节点还是有潜力的。也就是说你卷土重来时还是有机会的。
那么,当你回来时,你是否还要访问之前那些边呢?实际上没有必要了,易证。
那么,我们就可以记录一下当前这个节点遍历到哪一条出边,跑完后再重新开始。
这个优化就成为 当前弧优化。
(Tip:这个优化也适用于 Dinic,有很大的速度提升。)
同时,我们对于 ISAP 的高度很感兴趣。
因为高度相邻时,两条边才能算作连通。那么如果高度出现了断层,那么不就可以洗洗睡了吗?
所以,我们对于每一次 DFS 完毕后统计这个节点的高度增加后,会不会出现高度断层。出现了,就可以 over 了。
这个优化就被成为 Gap 优化。
加上了这辆个优化以后,我们的 ISAP 就所向披靡了。
建议大家以后都用 ISAP 做网络最大流问题。常数小,基本不可能跑满,没见过被卡,码量还很小。
最后给大家放上模板题的代码:
测试地址:(本题可以在洛谷上提交通过,没有吸氧)
趁现在赶紧白嫖一波双倍经验
// @author 5ab
/*
变量解释:
hd[],des[],val[],nxt[],edge_cnt:邻接表存图,不用解释,-1 代表末尾。
occ[p]:代表边 p 有多少流量被使用。
hei[i]:i 号点的高度。
gap[i]:高度为 i 的点的数量。
cur[i]:当前弧优化。
flag:是否出现断层取反,即是否可以继续。
*/
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
using namespace std;
const int max_n = 10000, max_m = 100000, INF = 2147483647;
int hd[max_n], des[max_m<<1], val[max_m<<1], occ[max_m<<1] = {}, nxt[max_m<<1], edge_cnt = 0;
int hei[max_n], gap[max_n] = {}, cur[max_n];
bool flag = true;
queue<int> q;
inline int my_min(int a, int b) { return (a < b)? a:b; }
int aug(int s, int t, int lim) // 深搜找最短增广路
{
if (s == t)
return lim;
if (!flag)
return 0;
int tmp, flow = 0;
for (int& p = cur[s]; p != -1; p = nxt[p])
if (hei[des[p]] == hei[s] - 1) // 高度差 1
{
tmp = aug(des[p], t, my_min(lim, val[p] - occ[p]));
flow += tmp, occ[p] += tmp, occ[p^1] -= tmp, lim -= tmp; // 正向边减权,反向边加权
if (lim <= 0)
return flow;
}
gap[hei[s]]--;
if (!gap[hei[s]])
flag = false; // 检测断层
hei[s]++, gap[hei[s]]++, cur[s] = hd[s];
return flow;
}
inline int read()
{
int ch = getchar(), n = 0, t = 1;
while (isspace(ch)) { ch = getchar(); }
if (ch == '-') { t = -1, ch = getchar(); }
while (isdigit(ch)) { n = n * 10 + ch - '0', ch = getchar(); }
return n * t;
}
void add_edge(int s, int t, int v)
{
des[edge_cnt] = t, val[edge_cnt] = v;
nxt[edge_cnt] = hd[s], hd[s] = edge_cnt++;
}
int main()
{
memset(hd, -1, sizeof(hd));
memset(hei, -1, sizeof(hei));
int n = read(), m = read(), s = read() - 1, t = read() - 1, ta, tb, tc, ans = 0, eg;
for (int i = 0; i < m; i++)
{
ta = read() - 1, tb = read() - 1, tc = read();
add_edge(ta, tb, tc); // 正向边
add_edge(tb, ta, 0); // 反向边
}
for (int i = 0; i < n; i++)
cur[i] = hd[i];
hei[t] = 0, gap[0] = 1;
q.push(t);
while (!q.empty()) // 宽搜分层
{
eg = q.front();
q.pop();
for (int p = hd[eg]; p != -1; p = nxt[p])
if (hei[des[p]] == -1)
{
hei[des[p]] = hei[eg] + 1;
gap[hei[des[p]]]++;
q.push(des[p]);
}
}
while (flag)
ans += aug(s, t, INF); // 不停寻找最短增广路
printf("%d\n", ans);
return 0;
}
后记
如果你能够一字不落地看完整篇笔记,希望你也能感受到发现算法的乐趣。
当然,如果你只是看完了代码,那么也恭喜你学会了一个新模板。
如果你只是看了标题,那么谢谢你给我白嫖了阅读数。
经过了将近 \(3\) 个小时的时间,终于写完了这篇笔记。
希望我的学习笔记能给你带来启发或是灵感。