第二篇 值函数Based——基于时间差分的强化学习方法

---

本分类专栏博客系列是学习《深入浅出强化学习原理入门》的学习总结。
书籍链接：链接：https://pan.baidu.com/s/1p0qQ68pzTb7_GK4Brcm4sw 提取码：opjy

---

---

基于时间差分的强化学习方法

1. 引入

我们已经阐述了⽆模型强化学习最基本的⽅法蒙特卡罗⽅法。本 章我们阐述另外⼀个⽆模型的⽅法：时间差分⽅法。

时间差分（Temporal-Difference，简称TD）⽅法（如图5.1所⽰）是另 ⼀种⽆模型强化学习⽅法，也是强化学习理论中最核⼼的内容。与动态规划的⽅法和蒙特卡罗的⽅法相⽐，时间差分⽅法的主要不同在于值函数的估计。

1.1 基于模型的动态规划方法回顾

如图5.2所⽰为⽤动态规划的⽅法计算值函数。

下⾯的式（5.1）是值函数估计的计算公式，从中可以看到，⽤动态规划⽅法（DP）计算值函数时⽤到了当前状态 $s$ 的所有后继状态 $s'$ 处的值函数。值函数的计算⽤到了bootstrapping的⽅法。所谓bootstrpping本意是指⾃举，此处是指当前值函数的计算⽤到了后继状态的值函数。即⽤后继状态的值函数估计当前值函数。要特别注意的是，此处后继的状态是由模型公式 $p(s',r|{S_t},a)$ 计算得到的。由模型公式和动作集，可以计算状态 $s$ 所有的后继状态 $s'$ 。当没有模型时，后继状态⽆法全部得到，只能通过试验和采样的⽅法每次试验得到⼀个后继状态 $s'$ 。

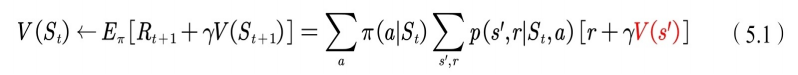
1.2 无模型的蒙特卡洛方法的回顾

⽆模型时，我们可以采⽤蒙特卡罗的⽅法利⽤经验平均来估计当前状态的值函数，⽤它计算值函数的过程如图5.3所⽰。

蒙特卡罗⽅法利⽤经验平均估计状态的值函数。此处的经验是指⼀次试验，⽽⼀次试验要等到终⽌状态出现才结束（参⻅图 5.3）。

先来讨论蒙特卡罗法求解强化学习预测问题的方法，即策略评估。一个给定策略 $π$ 的完整有 $T$ 个状态的状态序列如下：
$S_1,A_1,R_2,S_2,A_2,...,S_T,A_T,R_{t+1},...R_T,S_T$

回忆下马尔科夫决策过程(MDP)中对于价值函数 $v_π(s)$的定义:

${v_\pi }(s) = {E_\pi }({G_t}|{S_t} = s) = {E_\pi }({R_{t + 1}} + \gamma {R_{t + 2}} + {\gamma ^2}{R_{t + 3}} + ...|{S_t} = s)$

可以看出每个状态的价值函数等于所有该状态收获的期望，同时这个收获是通过后续的奖励与对应的衰减乘积求和得到。那么对于蒙特卡罗法来说，如果要求某一个状态的状态价值，只需要求出所有的完整序列中该状态出现时候的收获再取平均值即可近似求解，也就是：

${G_t} = {R_{t + 1}} + \gamma {R_{t + 2}} + {\gamma ^2}{R_{t + 3}} + ... + {\gamma ^{T - t - 1}}{R_T}$

${v_\pi }(s) = average({G_t}),$ $s.t.$ ${S_t} = s$

不过有几个点可以优化考虑。

• 第一个点是同样一个状态可能在一个完整的状态序列中重复出现，那么该状态的收获该如何计算？有两种解决方法。两种方法对应的蒙特卡罗法分别称为：首次访问(first visit) 和每次访问(every visit) 蒙特卡罗法。第一种是仅把状态序列中第一次出现该状态时的收获值纳入到收获平均值的计算中；另一种是针对一个状态序列中每次出现的该状态，都计算对应的收获值并纳入到收获平均值的计算中。第二种方法比第一种的计算量要大一些，但是在完整的经历样本序列少的场景下会比第一种方法适用。

• 第二个点是累进更新平均值（incremental mean)。在上面预测问题的求解公式里，我们有一个average的公式，意味着要保存所有该状态的收获值之和最后取平均。这样浪费了太多的存储空间。一个较好的方法是在迭代计算收获均值，即每次保存上一轮迭代得到的收获均值与次数，当计算得到当前轮的收获时，即可计算当前轮收获均值和次数。通过下面的公式就很容易理解这个过程：
  ${\mu _k} = \frac{1}{k}\sum\limits_{j = 1}^k {{x_j}} = \frac{1}{k}({x_k} + \sum\limits_{j = 1}^{k - 1} {{x_j}} ) = \frac{1}{k}({x_k} + (k - 1){\mu _{k - 1}}) = {\mu _{k - 1}} + \frac{1}{k}({x_k} - {\mu _{k - 1}})$

  这样上面的状态值公式就可以改写成：

   $\begin{array}{l} N(S_t) \leftarrow N(S_t) + 1\\ V({S_t}) = V({S_t}) + \frac{1}{{N(S_t)}}({G_t} - V({S_t})) \end{array}$

  公式中的 $G_t$ 是状态 $S_t$ 处的折扣累积回报值。

  有时候，尤其是海量数据做分布式迭代的时候，我们可能无法准确计算当前的次数 $N(S_t)$，这时我们可以用一个系数 $α$ 来代替，即：

   $V({S_t}) = V({S_t}) + α({G_t} - V({S_t}))$

  对于动作价值函数 $Q(S_t,A_t)$,也是类似的，比如对上面最后一个式子，动作价值函数版本为：

   $Q(S_t,A_t) \leftarrow Q(S_t,A_t)+α(G_t−Q(S_t,A_t))$

相⽐于动态规划的⽅法，蒙特卡罗的⽅法需要等到每次试验结束，所 以学习速度慢，学习效率不⾼。通过对两者的⽐较，我们很⾃然地会想 到：能不能借鉴动态规划中bootstrapping的⽅法，在试验未结束时就估计当 前的值函数呢？

答案是肯定的，这是时间差分⽅法的精髓。

2. 时间差分（TD）⽅法原理

2.1 TD基础

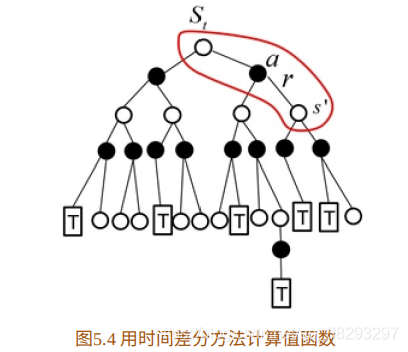
时间差分⽅法结合了蒙特卡罗的采样⽅法（即做试验）和动态规划⽅法的bootstrapping（利⽤后继状态的值函数估计当前值函数），它的计算过程如图5.4所⽰。

⽤时间差分⽅法（TD）将值函数的公式更新为

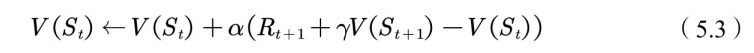
其中， ${R_{t + 1}} + \gamma V({S_{_{t + 1}}})$，称为 TD ⽬标，与上面中的 $G_t$ 相对应，两者不同之处是TD⽬标利⽤了bootstrapping⽅法估计当前值函数。 ${\delta _t} = {R_{t + 1}} + \gamma V({S_{_{t + 1}}}) - V({S_{_t}})$称为TD偏差。

2.2 DP、MC、TD的异同

下⾯我们从原始公式出发，了解动态规划（DP）、蒙特卡罗⽅法 （MC）和时间差分⽅法（TD）的不同之处。

图5.5是⽤三种⽅法估计值函数的异同点。从中可以看到，蒙特卡罗（MC）的⽅法使⽤的是值函数最原始的定义，该⽅法利⽤所有回报的累积和估计值函数；动态规划⽅法和时间差分⽅法则利⽤⼀步预测⽅法计算当前状态值函数，它俩的共同点是利⽤了bootstrapping ⽅法；不同的是，动态规划⽅法利⽤模型计算后继状态，时间差分⽅法利⽤试验得到后继状态。

从统计学的⾓来看，蒙特卡罗⽅法（MC）和时间差分⽅法（TD）都 是利⽤样本估计值函数的⽅法，哪种更好呢？既然都是统计⽅法，我们就可以从期望和⽅差两个指标对⽐两种⽅法。

⾸先我们先看看蒙特卡罗⽅法。

蒙特卡罗⽅法中的返回值 ${G_t} = {R_{t + 1}} + \gamma {R_{t + 2}} + ... + {\gamma ^{T - 1}}{R_T}$，其期望便是值函数的定义，因此蒙特卡罗⽅法是⽆偏估计。但是，蒙特卡罗⽅法每次得到的 $G_t$ 值要等到最终状态出现，在这个过程中会经历很多随机的状态和动作，每次得到的 $G_t$ 随机性很⼤，因此尽管期望等于真值，但⽅差⽆穷⼤。

我们再来看下时间差分⽅法。

时间差分⽅法的TD⽬标为 ${R_{t + 1}} + \gamma V({S_{t + 1}})$，若 $V({S_{t + 1}})$ 采⽤真实值，则TD估计也是⽆偏估计，然⽽在试验中 $V({S_{t + 1}})$ ⽤的也是估计值，因此时间差分估计⽅法属于有偏估计。与蒙特卡罗⽅法相⽐，时间差分⽅法只⽤到了⼀步随机状态和动作，因此TD⽬标的随机性⽐蒙特卡罗⽅法中的 $G_t$ 要⼩，相应的⽅差也⽐蒙特卡罗⽅法中的⽅差⼩。

2.3 同策略的Sarsa⽅法

时间差分⽅法包括同策略的Sarsa⽅法和异策略的Qlearning⽅法。

如图5.6所⽰为同策略Sarsa强化学习算法，需要注意的是⽅框中代码表⽰同策略中的⾏动策略和评估的策略都是 $ε-greedy$ 策略。与蒙特卡罗⽅法不同的是，它的值函数更新不同。

2.4 异策略的Qlearning⽅法

如图5.7所⽰为异策略的Qlearning⽅法。与Sarsa⽅法的不同之处在于,Qlearning⽅法是异策略的⽅法。即⾏动策略采⽤ $ε-greedy$ 策略，⽽⽬标策略为贪婪策略。

2.5 TD( $\lambda$)方法

TD⽅法除了常⽤的Sarsa⽅法和Qlearning⽅法，还包括 TD( $\lambda$) ⽅法，
下⾯我们详细阐述 TD( $\lambda$) ⽅法的来⻰去脉。

从图5.4我们看到，在更新当前值函数时，⽤到了下⼀个状态的值函数。我们可以据此推理，能否利⽤后继第⼆个状态的值函数来更新当前状态的值函数呢？

答案是肯定的，那么如何利⽤公式计算呢？

我们⽤ $G_t^{(1)} = {R_{t + 1}} + \gamma V({S_{t + 1}})$ 表⽰ TD ⽬标，利⽤第⼆步值函数来估计当前值函数可表⽰为 $G_t^{(2)} = {R_{t + 1}} + \gamma {R_{t + 2}} + {\gamma ^2}V({S_{t + 2}})$

以此类推，利⽤第n步的值函数更新当前值函数可表⽰为： $G_t^{(n)} = {R_{t + 1}} + \gamma {R_{t + 2}} + {\gamma ^2}{R_{t + 3}}+……{\gamma ^{n-1}}{R_{t + n}}+ {\gamma ^n}V({S_{t + n}})$

如图5.8所⽰为利⽤ $n$ 步值函数估计当前值函数的⽰意图。我们再审视⼀下刚才的结论：可以利⽤ $n$ 步值函数来估计当前值函数，也就是说当前值函数有 $n$ 种估计⽅法。

哪种估计值更接近真实值呢？

我们并不知道，但是可否利⽤加权的⽅法融合这 $n$ 个估计值？即 TD( $\lambda$) 方法。

在 $G_t^{(n)}$ 前乘以加权因⼦ $(1 - \lambda ){\lambda ^{n - 1}}$ ，之所以要乘以加权，原因在于

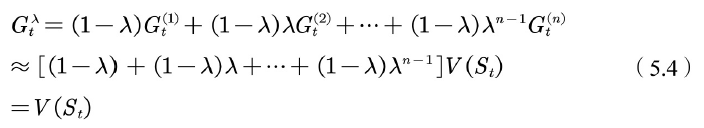
利⽤ $G_t^\lambda$ 更新当前状态的值函数的⽅法称为 TD( $\lambda$) 的⽅法。⼀般可以从前向和后向两个视⾓理解 。

2.5.1 前向观点

如图5.9所⽰为 TD( $\lambda$) ⽅法的前向视⾓解释。假设⼀个⼈坐在状态流上拿着望远镜看前⽅，前⽅是将来的状态。估计当前状态的值函数时，从 TD( $\lambda$) 的定义中可以看到，它需要⽤将来时刻的值函数。也就是说， TD( $\lambda$) 前向观点通过观看将来状态的值函数来估计当前的值函数。

第⼀个视⾓是前向视⾓，该视⾓也是 $G_t^\lambda$ 的定义。

其中，

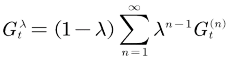
而

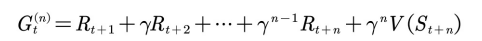
利⽤ TD( $\lambda$) 的前向观点估计值函数时，当前值函数的计算⽤到了将来时刻的值函数，因此需要整个试验结束后才能计算，这和蒙特卡罗⽅法相似。是否有某种更新⽅法不需要等到试验结束就可以更新当前状态的值函数？

有！这种增量式的更新⽅法需要利⽤ TD( $\lambda$) 的后向观点。

2.5.2 后向观点

如图 5.10 所⽰为 TD( $\lambda$) 后向观点⽰意图。⼈骑坐在状态流上，⼿⾥拿着话筒，⾯朝已经经历过的状态流，获得当前回报并利⽤下⼀个状态的值函数得到TD偏差后，此⼈会向已经经历过的状态喊话，告诉这些状态处的值函数需要利⽤当前时刻的 TD偏差更新。此时过往的每个状态值函数更新的⼤⼩应该与距离当前状态的步数有关。假设当前状态为 $s_t$ ，TD偏差为 ${\delta _t}$ ，那么 $s_{t-1}$ 处的值函数更新应该乘以⼀个衰减因⼦ $\gamma \lambda$，状态 $s_{t-2}$ 处的值函数更新应该乘以 $(\gamma \lambda)^2$，以此类推。

TD( $\lambda$) 更新过程如下。

⾸先，计算当前状态的TD偏差： ${\delta _t} = {R_{t + 1}} + \gamma V({S_{t + 1}}) - V({S_t})$
其次，更新适合度轨迹： ${E_t}(s) = \left\{ {\begin{array}{l} {\gamma \lambda {E_{t - 1}},s \ne {s_t}}\\ {\gamma \lambda {E_{t - 1}} + 1,s = {s_t}} \end{array}} \right.$

最后，对于状态空间中的每个状态 $s$，更新值函数： $V(s) \leftarrow V(s) + \alpha {\delta _t}{E_t}(s)$

其中 ${E_t}(s)$ 称为适合度轨迹。

2.5.3 前向观点和后向观点的异同

现在我们⽐较⼀下 TD( $\lambda$) 的前向观点和后向观点的异同。

（1）前向观点需要等到⼀次试验之后再更新当前状态的值函数；后向观点不需要等到值函数结束后再更新值函数，⽽是每⼀步都在更新值函数，是增量式⽅法。

（2）前向观点在⼀次试验结束后更新值函数时，更新完当前状态的值函数后，此状态的值函数就不再改变。后向观点在每⼀步计算完当前的TD误差后，其他状态的值函数需要利⽤当前状态的TD误差更新。

（3）在⼀次试验结束后，前向观点和后向观点每个状态的值函数的更新总量是相等的，都是 $G_t^\lambda$ 。

为了说明前向观点和后向观点的等价性，我们从公式上对其进⾏严格地证明。

⾸先，当 $\lambda = 0$ 时，只有当前状态值更新，此时等价于之前说的 TD ⽅法。所以TD⽅法⼜称为TD（0）⽅法。
其次，当 $\lambda = 1$ 时，状态 $s$ 值函数总的更新与蒙特卡罗⽅法下的更新总数相同：

对于⼀般的 $\lambda$ ，前向观点等于后向观点：

最后，我们给出 $Sarsa(\lambda )$ 算法的伪代码，如图5.11所⽰。