最长公共子序列长度（LCS）和最长上升子序列长度（LIS）问题的解法

概念理解

在了解LCS和LIS问题前，我们先来了解基本的概念

子序列
给定一个序列，将序列中0个或多个元素去掉之后得到的结果即为子序列。例如给定序列 $A = [1, 2, 3]$，那么 $A$ 的子序列有： $[]$， $[1]$， $[2]$， $[3]$， $[1,2]$， $[1,3]$， $[2,3]$， $[1,2,3]$。其概念类似数学集合的子集，区别是子序列可以有重复元素并且元素之间的相对顺序不能够改变。

最长子序列
一个序列的最长子序列等于它本身。例如给定序列 $A = [1, 2, 3]$，其最长子序列为 $[1,2,3]$。

最长公共子序列
最长公共子序列就是多个集合对应的子序列中，其共有的子序列中最长的那一个。例如给定序列 $A = [1, 3, 5, 8]$ 和序列 $B =[0, 1, 3, 8, 10]$，那么显然其最长公共子序列为 $[1, 3, 8]$。

最长上升子序列
最长上升子序列为一个集合所有的子序列中，元素大小递增的子序列。例如给定序列 $A = [10,9,2,5,3,7,101,18]$，那么其最长上升子序列是 $[2,3,7,101]$。

---

最长公共子序列（LCS）解法

题目

对于集合 $A = [A_1, A_2, ..., A_n]$， $B= [B_1,B_2,...,B_m]$，求出最长公共子序列 $LCS$ 集合的长度。

分析

上述集合中，集合 $A$ 的最后一个元素为 $A_n$ ，集合 $B$ 最后一个元素为 $A_m$
$LCS$ 具有以下性质：

• 如果集合 $A_n = B_m$ ：
  $LCS$的长度必然等于集合 $[A_0, A_1, ..., A_{n-1}]$和集合 $[B_0,B_1,...,B_{m - 1}]$的 $LCS$ 长度加上1。因为 $A_n$或者 $B_m$必然是 $LCS$集合中的一个元素，所以要加上1。
• 如果集合 $A_n\neq B_m$：
  定义集合 $[A_0, A_1, ..., A_{n-1}]$和集合 $[B_0,B_1,...,B_{m}]$的 $LCS$ 长度为 $L_1$ ；
  集合 $[A_0, A_1, ..., A_{n}]$和集合 $[B_0,B_1,...,B_{m - 1}]$的 $LCS$ 长度为 $L_2$。
  则 $LCS$ 的长度等于 $max\{L_1,L_2\}$ 。 因为 $A_n\neq B_m$，所以可以肯定 $LCS$ 的长度不会改变，所以也就只能在 $L_1$ 和 $L_2$ 选择一个更大的了。

上述规则显然是一个递推关系。为了求出 $A$ 和 $B$ 的 $LCS$ 长度，需要先求出集合 $A$ 中元素集合 $[A_0, A_1, ..., A_{n-1}]$和集合 $[B_0,B_1,...,B_{m - 1}]$的 $LCS$ 长度、集合 $[A_0, A_1, ..., A_{n-1}]$和集合 $[B_0,B_1,...,B_{m}]$的 $LCS$ 长度以及集合 $[A_0, A_1, ..., A_{n}]$和集合 $[B_0,B_1,...,B_{m - 1}]$的 $LCS$ 长度。所以可以考虑使用动态规划求解。

定义数组dp[i][j]为集合 $[A_0, A_1, ..., A_{i}]$和集合 $[B_0,B_1,...,B_{j}]$的 $LCS$ 长度，集合 $A$ 对应的数组为a，集合 $B$ 对应的数组为b。
那么dp[i][j]求法为：

• 如果a[i] == b[j]，那么dp[i][j] = dp[i-1][j-1] + 1；
• 如果a[i] != b[j]，那么dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

显然，dp[n][m]为数组a和数组b的 $LCS$ 长度。

建立好转移方程后，接下来需要考虑怎么填充dp数组：
显然，dp[i][j]的值依赖于dp[i - 1][j - 1]（左上角）、dp[i][j - 1]（左边）、dp[i - 1][j]（上方），所以可以考虑使用二次循环，从左上角开始，从左至右，从上到下填表，时间复杂度为 $O(N^2)$：

最终代码

public int solve(int[] a, int[] b) {
	int n = a.length;
	int m = b.length;
	int[][] dp = new int[n + 1][m + 1];
	for(int i = 1; i <= n; i++) {  
		for(int j = 1; j <= m; j++) {
			if(a[i - 1] == b[j - 1]) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			} else {
				dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}
	return dp[n][m];
}

练习题

LeetCode 1143

---

最长上升子序列（LIS）解法

题目

对于集合 $A = [A_1, A_2, ..., A_n]$，求出集合 $A$ 的最长上升子序列。

分析

考虑使用动态规划，大多数人会首先将dp[m]定义为集合 $[A_1, A_2, ..., A_m]$ 中 最长上升子序列的长度。因为最长上升子序列在数组中并不是连续的，所以dp[m]和dp[m - 1]并没有直接的递推关系。

不妨换个思路，我们可以定义dp[m]为以元素 $A_m$结尾可以获得的最长上升子序列，也就是说，这个最长上升子序列必然包含元素 $A_m$，且 $A_m$ 是这个最长上升子序列当中的最大值。在求出dp[0]到dp[n]后，dp[0]到dp[n]中的最大值即为集合 $A$ 的最长上升子序列长度。

那么具体怎么求dp[m]呢？
首先不论怎样，dp[m]的最小值肯定为1，因为根据dp[m]的定义必然包含元素 $A_m$。

既然要求出以元素 $A_m$结尾可以获得的最长上升子序列长度，那么我们需要找出前面结尾比 $A_m$ 小的上升子序列，这些上升子序列肯定是可以接到 $A_m$ 前面的，从而生成一个更大的上升子序列，并且这个新的子序列长度会大上1（因为这个子序列末尾为 $A_m$）。

用代码表示就是：

dp[m] = 1;
for(int i = 0; i < m; i++) {  //dp[m] = max(dp[i] + 1)
	if(arr[i] < arr[m]) {
		dp[m] = Math.max(dp[m], dp[i] + 1);  
	}
}

如果还不懂可以看下面这个图：

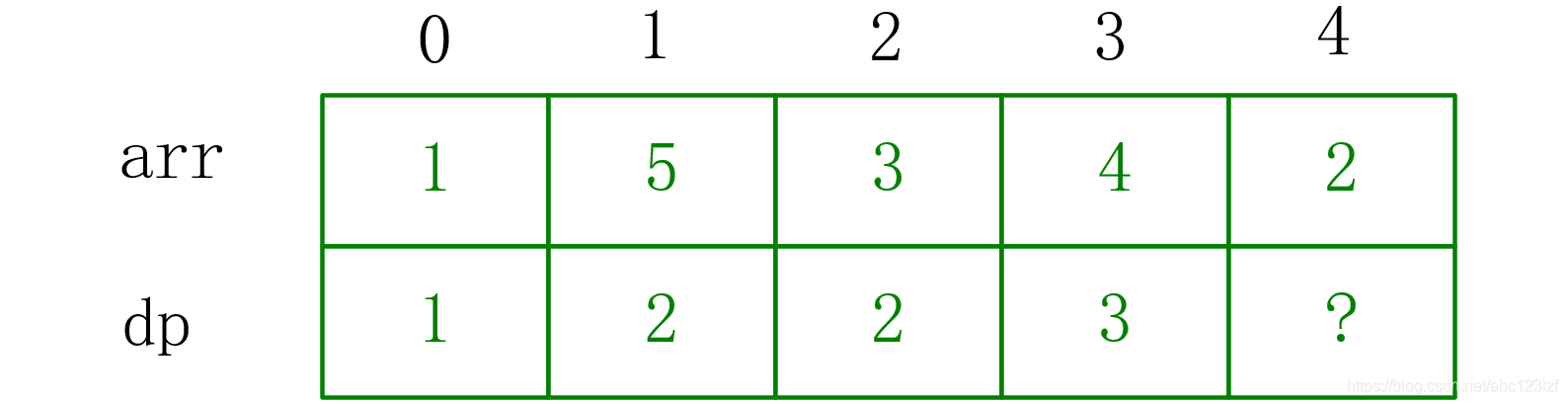
已知dp[0]~dp[3]的结果，如何求出dp[4]？
首先dp[4]含义是以2为结尾的最长上升子序列，所以这个最长上升子序列前面的值必然比2要小。
我们从0开始：

• i == 0，发现arr[0] < 2，所以这个arr[0]可以作为以2为结尾的最长子序列当中的一个元素，此时最长子序列为 $[1, 2]$。而以arr[0]也就是1为结尾的最长子序列长度为dp[0]也就是1，所以将dp[4]更新为dp[0] + 1也就是2。
• i == 1，发现arr[1] > 2，所以这个arr[1]不能够放在2的前面，略过。
• i == 2，发现arr[2] > 2，所以这个arr[2]不能够放在2的前面，略过。
• i == 3，发现arr[3] > 2，所以这个arr[3]不能够放在2的前面，略过。

所以最终dp[4]的值为2.

计算完dp数组所有内容后，我们遍历dp数组，以最大的值为本题的答案。该算法的时间复杂度为 $O(N^2)$。

最终代码

public int solve(int[] arr) {
	int n = arr.length;
    if(n == 0) {
        return 0;
    }
    int[] dp = new int[n];
    Arrays.fill(dp, 1); //dp所有元素设为1
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            if(arr[j] < arr[i]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }

    int ans = 1;
    for (int i = 0; i < n; i++) {
        ans = Math.max(dp[i], ans);
    }

    return ans;
}