优化算法note

发展：

优化算法的主要步骤：

SGD：

• 下降梯度就是最简单的
• 最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点。

SGD with Momentum

• 下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些
• 引入了一阶动:一阶动量是各个时刻梯度方向的指数移动平均值，约等于最近 1/(1 - β) 个时刻的梯度向量和的平均值。

也就是说，t时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定。β 的经验值为0.9，这就意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。

但是想象高速公路上汽车转弯，在高速向前的同时略微偏向，急转弯可是要出事的。

SGD with Nesterov Acceleration

SGD 还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地，四周都是略高的小山，你觉得没有下坡的方向，那就只能待在这里了。可是如果你爬上高地，就会发现外面的世界还很广阔。因此，我们不能停留在当前位置去观察未来的方向，而要向前一步、多看一步、看远一些。

NAG全称Nesterov Accelerated Gradient，是在SGD、SGD-M的基础上的进一步改进，改进点在于步骤1。**我们知道在时刻t的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度方向，不如先看看如果跟着累积动量走了一步，那个时候再怎么走。**因此，NAG在步骤1，不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，那个时候的下降方向：

$g_t = \nabla f(w_t - α·m_{t-1} / \sqrt{V_{t-1}})$

然后用下一个点的梯度方向，与历史累积动量相结合，计算步骤2中当前时刻的累积动量。

AdaGrad

此前我们都没有用到二阶动量。二阶动量的出现，才意味着“自适应学习率”优化算法时代的到来。

SGD及其变种以同样的学习率更新每个参数，但深度神经网络往往包含大量的参数，这些参数并不是总会用得到（想想大规模的embedding）。对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。

怎么样去度量历史更新频率呢？那就是二阶动量——该维度上，迄今为止所有梯度值的平方和：

回顾一下步骤3中的下降梯度

可以看出，此时实质上的学习率由 α 变成 α/ $\sqrt V_t$。一般为了避免分母为0，会在分母上加一个小的平滑项。因此 $\sqrt V_t$ 是恒大于0的，而且参数更新越频繁，二阶动量越大，学习率就越小。

• 这一方法在稀疏数据场景下表现非常好。
• 但也存在一些问题：因为 $\sqrt V_t$是单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。
• 当梯度一直不为0时，Adagrad的自适应学习率的分母会不断累加，使自适应学习率趋于0，出现梯度消息的问题

AdaDelta / RMSProp

由于AdaGrad单调递减的学习率变化过于激进，我们考虑一个改变二阶动量计算方法的策略：不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。

修改的思路很简单。前面我们讲到，指数移动平均值大约就是过去一段时间的平均值，因此我们用这一方法来计算二阶累积动量：

$V_t = β_2 * V_{t-1} + (1 - β_2)g_t^2$

这就避免了二阶动量持续累积、导致训练过程提前结束的问题了。

Reference

• Adelta是基于RMSprop的改进，只需传入EMA的衰减参数

• RMSProp不是直接对梯度平方进行累加，而是使用EMA对上一时刻的自适应学习率的分母进行衰减

Adam

Adam和Nadam是前述方法的集大成者。我们看到，SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。

SGD的一阶动量：

$m_t = β_1·m_{t-1}+(1-β_1)·g_t$

加上AdaDelta的二阶动量：

$V_t = β_2 * V_{t-1} + (1 - β_2)g_t^2$

优化算法里最常见的两个超参数 $β_1$ $β_2$ 就都在这里了，前者控制一阶动量，后者控制二阶动量。

Nadam

Nesterov + Adam = Nadam

Reference:

https://zhuanlan.zhihu.com/p/32230623

https://ruder.io/optimizing-gradient-descent/

两张经典的动图

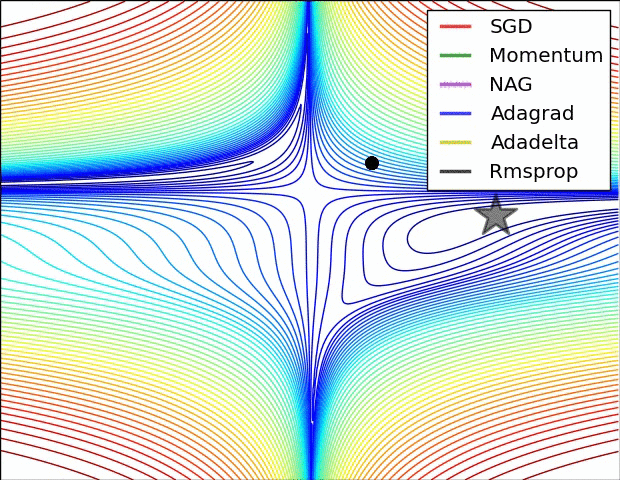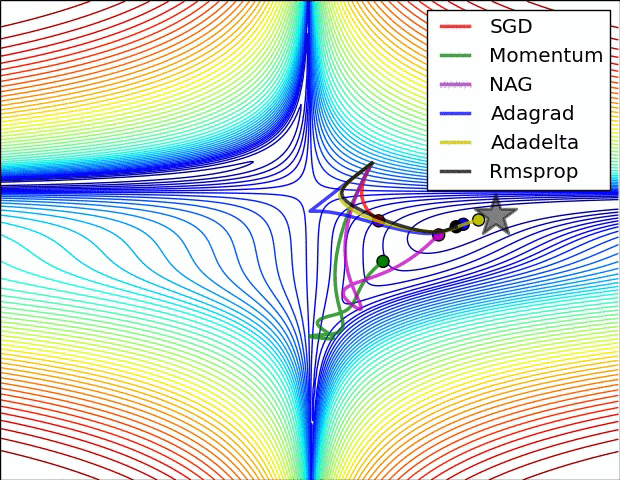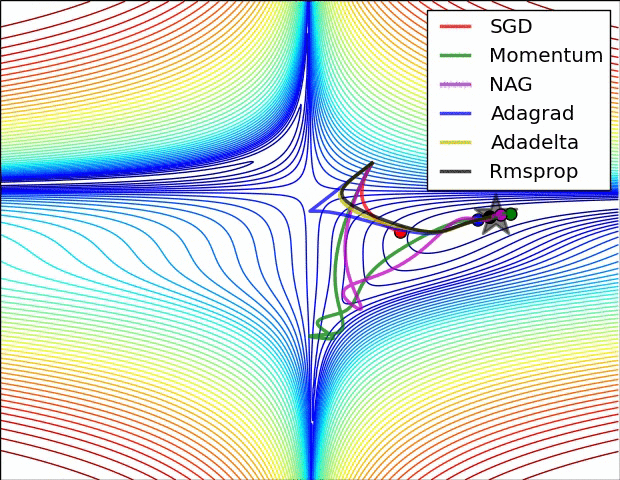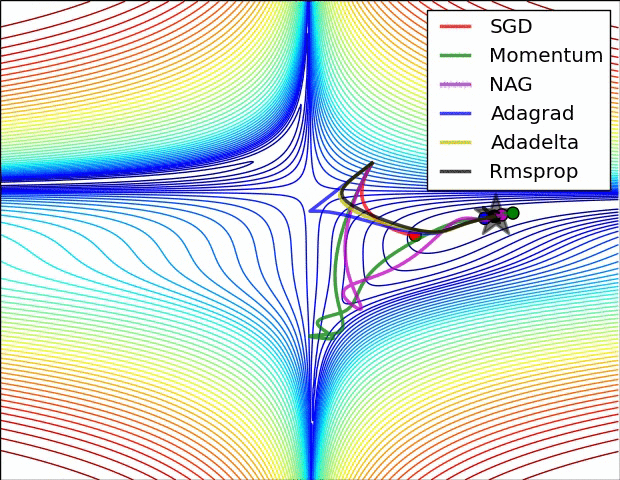
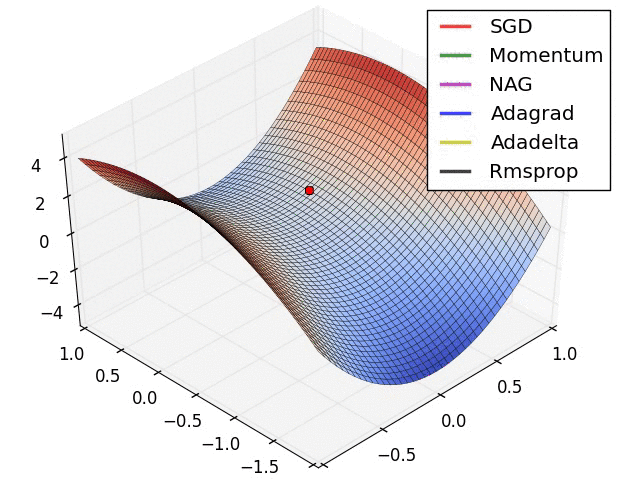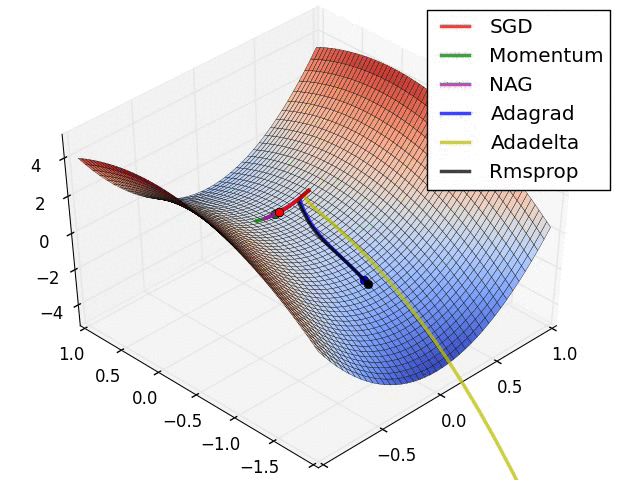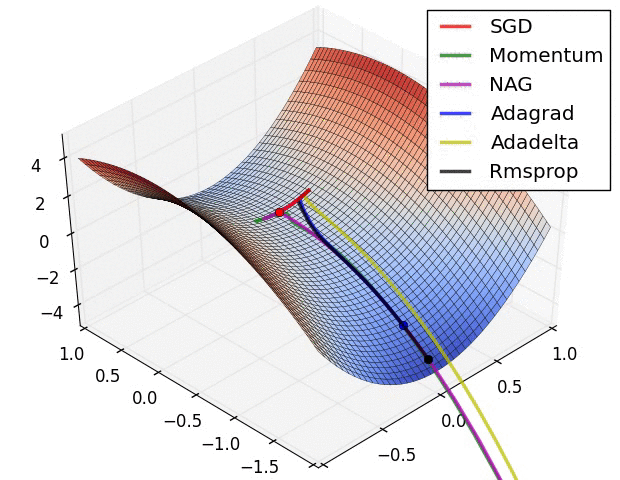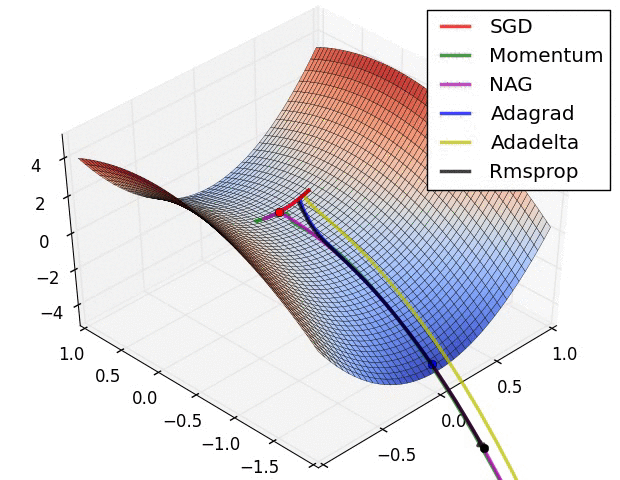
详细分解

梯度下降

存在问题：

计算梯度并更新参数为如下公式：

每次梯度更新的时候都会更新−εg，这个恒定的值会带来很多麻烦

• 参数过小时，这会造成自变量在水平方向上朝最优解移动变慢。

可以看到，同一位置上，目标函数在竖直方向（ x2 轴方向）比在水平方向（ x1 轴方向）的斜率的绝对值更大。因此，给定学习率，梯度下降迭代自变量时会使自变量在竖直方向比在水平方向移动幅度更大。而且初期耗费不必要的时间。

• 参数过大时，如果梯度下降过程中太陡峭，那么下降时就会一直震荡。

自变量在竖直方向不断越过最优解并逐渐发散

综合上述问题提出Momentum

Momentum

在 Section 11.4 中，我们提到，目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向。因此，梯度下降也叫作最陡下降（steepest descent）。在每次迭代中，梯度下降根据自变量当前位置，沿着当前位置的梯度更新自变量。然而，如果自变量的迭代方向仅仅取决于自变量当前位置，这可能会带来一些问题。对于noisy gradient,我们需要谨慎的选取学习率和batch size, 来控制梯度方差和收敛的结果。

$\mathbf{g}_t = \partial_{\mathbf{w}} \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} f(\mathbf{x}_{i}, \mathbf{w}_{t-1}) = \frac{1}{|\mathcal{B}_t|} \sum_{i \in \mathcal{B}_t} \mathbf{g}_{i, t-1}.$

简单来说

• 引入了v这个概念，其实这个v就是梯度的改变量

计算梯度并更新参数为如下公式：

经过上述操作， 梯度的变化量的推导公式如下所示

第一次迭代公式如下，其中v1=−εg1

第二次迭代公式如下

通过第二个公式可以得到：

• 如果本次和上次的梯度符号是相同的，那么就能够加速下降（幅度变大），就能够解决原先下降太慢的问题；
• 如果本次和上次的梯度符号是相反的，那么这次就和上次相互抑制，减缓震荡。

从而解决梯度下降原始的两个问题

涉及的知识

指数加权移动平均（exponential moving average）

给定超参数 $0 \leq \beta < 1$，当前时间步 $t$ 的变量 $y_t$ 是上一时间步 $t-1$ 的变量 $y_{t-1}$ 和当前时间步另一变量 $x_t$ 的线性组合：

$y_t = \beta y_{t-1} + (1-\beta) x_t.$

我们可以对 $y_t$ 展开：

$\begin{aligned} y_t &= (1-\beta) x_t + \beta y_{t-1}\\ &= (1-\beta)x_t + (1-\beta) \cdot \beta x_{t-1} + \beta^2y_{t-2}\\ &= (1-\beta)x_t + (1-\beta) \cdot \beta x_{t-1} + (1-\beta) \cdot \beta^2x_{t-2} + \beta^3y_{t-3}\\ &= (1-\beta) \sum_{i=0}^{t} \beta^{i}x_{t-i} \end{aligned}$

$(1-\beta)\sum_{i=0}^{t} \beta^{i} = \frac{1-\beta^{t}}{1-\beta} (1-\beta) = (1-\beta^{t})$

Supp

Approximate Average of $\frac{1}{1-\beta}$ Steps

令 $n = 1/(1-\beta)$，那么 $\left(1-1/n\right)^n = \beta^{1/(1-\beta)}$。因为

$\lim_{n \rightarrow \infty} \left(1-\frac{1}{n}\right)^n = \exp(-1) \approx 0.3679,$

所以当 $\beta \rightarrow 1$时， $\beta^{1/(1-\beta)}=\exp(-1)$，如 $0.95^{20} \approx \exp(-1)$。如果把 $\exp(-1)$ 当作一个比较小的数，我们可以在近似中忽略所有含 $\beta^{1/(1-\beta)}$ 和比 $\beta^{1/(1-\beta)}$ 更高阶的系数的项。例如，当 $\beta=0.95$ 时，

$y_t \approx 0.05 \sum_{i=0}^{19} 0.95^i x_{t-i}.$

因此，在实际中，我们常常将 $y_t$ 看作是对最近 $1/(1-\beta)$ 个时间步的 $x_t$ 值的加权平均。例如，当 $\gamma = 0.95$ 时， $y_t$ 可以被看作对最近20个时间步的 $x_t$ 值的加权平均；当 $\beta = 0.9$ 时， $y_t$ 可以看作是对最近10个时间步的 $x_t$ 值的加权平均。而且，离当前时间步 $t$ 越近的 $x_t$ 值获得的权重越大（越接近1）。

由指数加权移动平均理解动量法

现在，我们对动量法的速度变量做变形：

$\boldsymbol{m}_t \leftarrow \beta \boldsymbol{m}_{t-1} + (1 - \beta) \left(\frac{\eta_t}{1 - \beta} \boldsymbol{g}_t\right).$

Another version:

$\boldsymbol{m}_t \leftarrow \beta \boldsymbol{m}_{t-1} + (1 - \beta) \boldsymbol{g}_t.$

$\begin{aligned} \boldsymbol{x}_t &\leftarrow \boldsymbol{x}_{t-1} - \alpha_t \boldsymbol{m}_t, \end{aligned}$

$\alpha_t = \frac{\eta_t}{1-\beta}$

由指数加权移动平均的形式可得，速度变量 $\boldsymbol{v}_t$ 实际上对序列 $\{\eta_{t-i}\boldsymbol{g}_{t-i} /(1-\beta):i=0,\ldots,1/(1-\beta)-1\}$ 做了指数加权移动平均。换句话说，相比于小批量随机梯度下降，动量法在每个时间步的自变量更新量近似于将前者对应的最近 $1/(1-\beta)$ 个时间步的更新量做了指数加权移动平均后再除以 $1-\beta$。所以，在动量法中，自变量在各个方向上的移动幅度不仅取决当前梯度，还取决于过去的各个梯度在各个方向上是否一致。在本节之前示例的优化问题中，所有梯度在水平方向上为正（向右），而在竖直方向上时正（向上）时负（向下）。这样，我们就可以使用较大的学习率，从而使自变量向最优解更快移动。

总结

相对于小批量随机梯度下降，动量法需要对每一个自变量维护一个同它一样形状的速度变量，且超参数里多了动量超参数。实现中，我们将速度变量用更广义的状态变量states表示。

在Pytorch中，torch.optim.SGD已实现了Momentum。

AdaGrad

在momentum一节里我们看到当 $x_1$和 $x_2$的梯度值有较大差别时，需要选择足够小的学习率使得自变量在梯度值较大的维度上不发散。

• 但这样会导致自变量在梯度值较小的维度上迭代过慢。动量法依赖指数加权移动平均使得自变量的更新方向更加一致，从而降低发散的可能。

而AdaGrad算法，它根据自变量在每个维度的梯度值的大小来调整各个维度上的学习率，从而避免统一的学习率难以适应所有维度的问题。

Algorithm

AdaGrad算法会使用一个小批量随机梯度 $\boldsymbol{g}_t$按元素平方的累加变量 $\boldsymbol{s}_t$。在时间步0，AdaGrad将 $\boldsymbol{s}_0$中每个元素初始化为0。在时间步 $t$，首先将小批量随机梯度 $\boldsymbol{g}_t$按元素平方后累加到变量 $\boldsymbol{s}_t$：

$\boldsymbol{s}_t \leftarrow \boldsymbol{s}_{t-1} + \boldsymbol{g}_t \odot \boldsymbol{g}_t,$

其中 $\odot$是按元素相乘。接着，我们将目标函数自变量中每个元素的学习率通过按元素运算重新调整一下：

$\boldsymbol{x}_t \leftarrow \boldsymbol{x}_{t-1} - \frac{\eta}{\sqrt{\boldsymbol{s}_t + \epsilon}} \odot \boldsymbol{g}_t,$

其中 $\eta$是学习率， $\epsilon$是为了维持数值稳定性而添加的常数，如 $10^{-6}$。这里开方、除法和乘法的运算都是按元素运算的。这些按元素运算使得目标函数自变量中每个元素都分别拥有自己的学习率。

Feature

需要强调的是，小批量随机梯度按元素平方的累加变量 $\boldsymbol{s}_t$出现在学习率的分母项中。因此，如果目标函数有关自变量中某个元素的偏导数一直都较大，那么该元素的学习率将下降较快；反之，如果目标函数有关自变量中某个元素的偏导数一直都较小，那么该元素的学习率将下降较慢。然而，由于 $\boldsymbol{s}_t$一直在累加按元素平方的梯度，自变量中每个元素的学习率在迭代过程中一直在降低（或不变）。所以，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。

同动量法一样，AdaGrad算法需要对每个自变量维护同它一样形状的状态变量。我们根据AdaGrad算法中的公式实现该算法。

11.8 RMSProp

我们在“AdaGrad算法”一节中提到，因为调整学习率时分母上的变量 $\boldsymbol{s}_t$一直在累加按元素平方的小批量随机梯度，所以目标函数自变量每个元素的学习率在迭代过程中一直在降低（或不变）。因此，当学习率在迭代早期降得较快且当前解依然不佳时，AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。为了解决这一问题，RMSProp算法对AdaGrad算法做了修改。该算法源自Coursera上的一门课程，即“机器学习的神经网络”。

Algorithm

我们在“动量法”一节里介绍过指数加权移动平均。不同于AdaGrad算法里状态变量 $\boldsymbol{s}_t$是截至时间步 $t$所有小批量随机梯度 $\boldsymbol{g}_t$按元素平方和，RMSProp算法将这些梯度按元素平方做指数加权移动平均。具体来说，给定超参数 $0 \leq \gamma 0$计算

$\boldsymbol{v}_t \leftarrow \beta \boldsymbol{v}_{t-1} + (1 - \beta) \boldsymbol{g}_t \odot \boldsymbol{g}_t.$

和AdaGrad算法一样，RMSProp算法将目标函数自变量中每个元素的学习率通过按元素运算重新调整，然后更新自变量

$\boldsymbol{x}_t \leftarrow \boldsymbol{x}_{t-1} - \frac{\alpha}{\sqrt{\boldsymbol{v}_t + \epsilon}} \odot \boldsymbol{g}_t,$

其中 $\eta$是学习率， $\epsilon$是为了维持数值稳定性而添加的常数，如 $10^{-6}$。因为RMSProp算法的状态变量 $\boldsymbol{s}_t$是对平方项 $\boldsymbol{g}_t \odot \boldsymbol{g}_t$的指数加权移动平均，所以可以看作是最近 $1/(1-\beta)$个时间步的小批量随机梯度平方项的加权平均。如此一来，自变量每个元素的学习率在迭代过程中就不再一直降低（或不变）。

照例，让我们先观察RMSProp算法对目标函数 $f(\boldsymbol{x})=0.1x_1^2+2x_2^2$中自变量的迭代轨迹。回忆在“AdaGrad算法”一节使用的学习率为0.4的AdaGrad算法，自变量在迭代后期的移动幅度较小。但在同样的学习率下，RMSProp算法可以更快逼近最优解。

11.9 AdaDelta

除了RMSProp算法以外，另一个常用优化算法AdaDelta算法也针对AdaGrad算法在迭代后期可能较难找到有用解的问题做了改进 [1]。有意思的是，AdaDelta算法没有学习率这一超参数。

Algorithm

AdaDelta算法也像RMSProp算法一样，使用了小批量随机梯度 $\boldsymbol{g}_t$按元素平方的指数加权移动平均变量 $\boldsymbol{s}_t$。在时间步0，它的所有元素被初始化为0。给定超参数 $0 \leq \rho 0$，同RMSProp算法一样计算

$\boldsymbol{s}_t \leftarrow \rho \boldsymbol{s}_{t-1} + (1 - \rho) \boldsymbol{g}_t \odot \boldsymbol{g}_t.$

与RMSProp算法不同的是，AdaDelta算法还维护一个额外的状态变量 $\Delta\boldsymbol{x}_t$，其元素同样在时间步0时被初始化为0。我们使用 $\Delta\boldsymbol{x}_{t-1}$来计算自变量的变化量：

$\boldsymbol{g}_t' \leftarrow \sqrt{\frac{\Delta\boldsymbol{x}_{t-1} + \epsilon}{\boldsymbol{s}_t + \epsilon}} \odot \boldsymbol{g}_t,$

其中 $\epsilon$是为了维持数值稳定性而添加的常数，如 $10^{-5}$。接着更新自变量：

$\boldsymbol{x}_t \leftarrow \boldsymbol{x}_{t-1} - \boldsymbol{g}'_t.$

最后，我们使用 $\Delta\boldsymbol{x}_t$来记录自变量变化量 $\boldsymbol{g}'_t$按元素平方的指数加权移动平均：

$\Delta\boldsymbol{x}_t \leftarrow \rho \Delta\boldsymbol{x}_{t-1} + (1 - \rho) \boldsymbol{g}'_t \odot \boldsymbol{g}'_t.$

可以看到，如不考虑 $\epsilon$的影响，AdaDelta算法与RMSProp算法的不同之处在于使用 $\sqrt{\Delta\boldsymbol{x}_{t-1}}$来替代超参数 $\eta$。

Implement

AdaDelta算法需要对每个自变量维护两个状态变量，即 $\boldsymbol{s}_t$和 $\Delta\boldsymbol{x}_t$。我们按AdaDelta算法中的公式实现该算法。

11.10 Adam

Adam算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均 [1]。下面我们来介绍这个算法。

Algorithm

Adam算法使用了动量变量 $\boldsymbol{m}_t$和RMSProp算法中小批量随机梯度按元素平方的指数加权移动平均变量 $\boldsymbol{v}_t$，并在时间步0将它们中每个元素初始化为0。给定超参数 $0 \leq \beta_1 < 1$（算法作者建议设为0.9），时间步 $t$的动量变量 $\boldsymbol{m}_t$即小批量随机梯度 $\boldsymbol{g}_t$的指数加权移动平均：

$\boldsymbol{m}_t \leftarrow \beta_1 \boldsymbol{m}_{t-1} + (1 - \beta_1) \boldsymbol{g}_t.$

和RMSProp算法中一样，给定超参数 $0 \leq \beta_2 < 1$（算法作者建议设为0.999），
将小批量随机梯度按元素平方后的项 $\boldsymbol{g}_t \odot \boldsymbol{g}_t$做指数加权移动平均得到 $\boldsymbol{v}_t$：

$\boldsymbol{v}_t \leftarrow \beta_2 \boldsymbol{v}_{t-1} + (1 - \beta_2) \boldsymbol{g}_t \odot \boldsymbol{g}_t.$

由于我们将 $\boldsymbol{m}_0$和 $\boldsymbol{s}_0$中的元素都初始化为0，
在时间步 $t$我们得到 $\boldsymbol{m}_t = (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} \boldsymbol{g}_i$。将过去各时间步小批量随机梯度的权值相加，得到 $(1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} = 1 - \beta_1^t$。需要注意的是，当 $t$较小时，过去各时间步小批量随机梯度权值之和会较小。例如，当 $\beta_1 = 0.9$时， $\boldsymbol{m}_1 = 0.1\boldsymbol{g}_1$。为了消除这样的影响，对于任意时间步 $t$，我们可以将 $\boldsymbol{m}_t$再除以 $1 - \beta_1^t$，从而使过去各时间步小批量随机梯度权值之和为1。这也叫作偏差修正。在Adam算法中，我们对变量 $\boldsymbol{m}_t$和 $\boldsymbol{v}_t$均作偏差修正：

$\hat{\boldsymbol{m}}_t \leftarrow \frac{\boldsymbol{m}_t}{1 - \beta_1^t},$

$\hat{\boldsymbol{v}}_t \leftarrow \frac{\boldsymbol{v}_t}{1 - \beta_2^t}.$

接下来，Adam算法使用以上偏差修正后的变量 $\hat{\boldsymbol{m}}_t$和 $\hat{\boldsymbol{m}}_t$，将模型参数中每个元素的学习率通过按元素运算重新调整：

$\boldsymbol{g}_t' \leftarrow \frac{\eta \hat{\boldsymbol{m}}_t}{\sqrt{\hat{\boldsymbol{v}}_t} + \epsilon},$

其中 $\eta$是学习率， $\epsilon$是为了维持数值稳定性而添加的常数，如 $10^{-8}$。和AdaGrad算法、RMSProp算法以及AdaDelta算法一样，目标函数自变量中每个元素都分别拥有自己的学习率。最后，使用 $\boldsymbol{g}_t'$迭代自变量：

$\boldsymbol{x}_t \leftarrow \boldsymbol{x}_{t-1} - \boldsymbol{g}_t'.$

Implement

我们按照Adam算法中的公式实现该算法。其中时间步 $t$通过hyperparams参数传入adam函数。