直接最小二乘法拟合椭圆

直接最小二乘法拟合椭圆

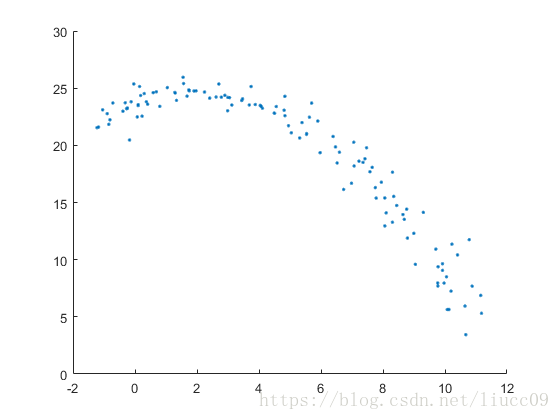
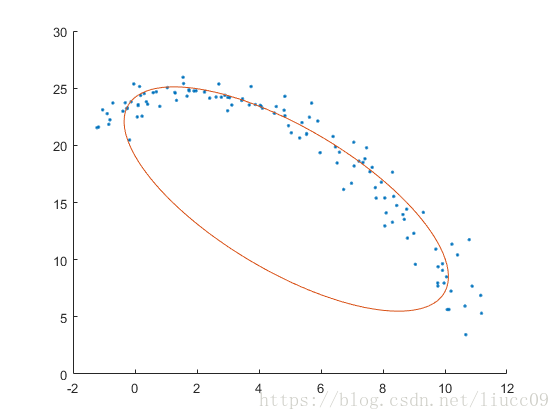
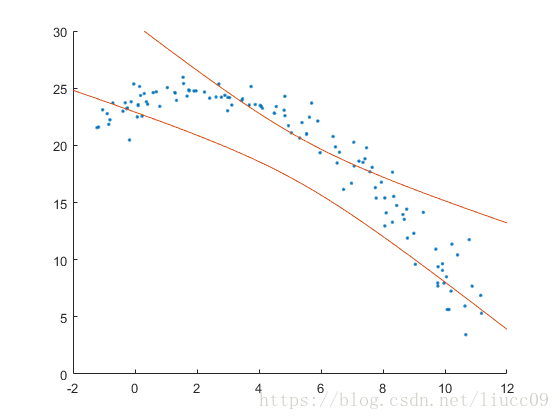
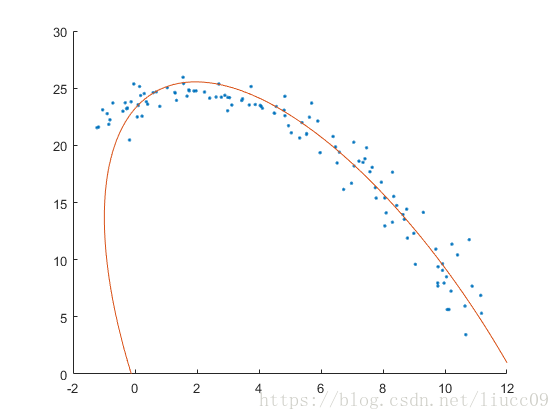
利用最小二乘算法构造方程，使用拉格朗日乘子进行求解

椭圆方程

$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$

优化目标

令 $W=\left[A,B,C,D,E,F\right]^\top$， $X=\left[x^2,xy,y^2,x,y,1\right]^\top$，则优化目标为
$\min\left\|{W^\top X }\right\|^2 =W^\top X X^\top W\\ s.t. \quad W^\top H W>0$
其中 $H = \begin{bmatrix} 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}$
$\quad W^\top H W>0$是椭圆参数约束 $4AC-B^2>0$

由于 $\left\|{W^\top X }\right\|^2=0$时， $W$可以有一个缩放因子，即所有 $W^\prime = \alpha W$也同样满足条件，因此我们让 $\quad W^\top H W=1$

于是优化目标变为：
$\min\left\|{W^\top X }\right\|^2 =W^\top X X^\top W\\ s.t. \quad W^\top H W=1$

拉格朗日函数

构造拉格朗日函数
$L\left(W,\lambda\right)=W^\top X X^\top W-\lambda \left( W^\top H W-1\right)$
对其求导得零：
$\frac{{\partial L}}{{\partial W}} = 0$
即
$XX^\top W-\lambda HW = 0 \Rightarrow XX^\top W=\lambda HW$
令 $S=XX^\top$，则 $SW=\lambda HW$，通过求解广义特征向量可以得到6个可能的备选 $W$。然后需要用到 $W^\top H W=1$这个条件来筛选合格的 $W$。由于 $uW$也满足 $SuW=\lambda HuW$，要使 $uW^\top HuW=1$则 $u=\sqrt{\frac{1}{W^\top HW}}=\sqrt{\frac{\lambda}{W^\top SW}}$，由于 $S$是正定矩阵，所以 ${\lambda>0}$。因此在特征值大于0的特征向量里面选出那些实特征向量即可满足要求，并计算对应的缩放系数 $u$。详见论文"Direct least square fitting of ellipses"。

如果不求广义特征向量，由于 $S$为正定矩阵，也可以将 $S$的逆乘到左右两边，得
${S^{ - 1}}HW = \frac{1}{\lambda }W$
这就转换为求解特征向量的问题。

更早的一种直接拟合法

优化目标

$\min\left\|{W^\top X }\right\|^2 =W^\top X X^\top W\\ s.t. \quad W^\top W=1$
这里 $W^\top W=1$是为了避免 $W=0$的情形，但也可以看出，这种方法不能保证结果一定是椭圆，可能是其他二次曲线。

拉格朗日函数

构造拉格朗日函数
$L\left(W\right)=W^\top X X^\top W-\lambda \left( W^\top W-1\right)$
对其求导得零：
$\frac{{\partial L}}{{\partial W}} = 0$
即
$XX^\top W-\lambda W = 0 \Rightarrow XX^\top W=\lambda W \Rightarrow S W=\lambda W$
然后求解 $S$的特征向量即可，但由于有6个特征向量，因此需要筛选符合要求的特征向量

筛选符合要求的特征向量

假设得到特征值和特征向量对 $\left\{ {{\lambda _i},{v_i}} \right\}$

此外，对于椭圆方程
$ax^2+2hxy+by^2+2gx+2fy+c=0$
判别式
$\Delta=\begin{vmatrix} a&h&g \\ h&b&f \\ g&f&c \\ \end{vmatrix}=abc+2fgh-af^2-bg^2-ch^2$
当 $\Delta\ne0$，且 $ab-h^2>0$时为椭圆

条件一： $\Delta\ne0$

条件二： $ab-h^2>0$ 或 $v_i^\top Hv_i>0$

对于实椭圆， $\frac{\Delta}{a+b}<0$

条件三： $\frac{\Delta}{a+b}<0$

符合上面三个条件的特征向量可以作为椭圆方程的参数

还有另一种筛选方法，但不如上述方法严格，由于 $W^\top XX^\top W$为二次误差，那么使二次误差最小的特征向量应该是椭圆的参数向量。由于
$XX^\top W=\lambda W \Rightarrow W^\top XX^\top W = \lambda W^\top W$
而 $W^\top H W>0$，所以最小的特征值 $\lambda_i$对应的特征向量即为椭圆参数向量。

根据椭圆一般方程求解椭圆参数

椭圆方程：
$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$
几何中心：
$\begin{aligned} X_c&=\frac{BE-2CD}{4AC-B^2}\\ Y_c&=\frac{BD-2AE}{4AC-B^2} \end{aligned}$
长半轴短半轴：
$\begin{aligned} A^2 = \frac{2\left(AX_c^2+CY_c^2+BX_cY_c-F\right)}{A+C+\sqrt{\left(A-C\right)^2+B^2}}\\ B^2 = \frac{2\left(AX_c^2+CY_c^2+BX_cY_c-F\right)}{A+C-\sqrt{\left(A-C\right)^2+B^2}} \end{aligned}$
长轴倾角：
$\theta=\frac{1}{2}\arctan\frac{B}{A-C}$
上述方法有可能求出来的是短轴的倾角，因为公式并没有区分两个轴的长短，更稳妥的算法如下方python代码所示：

#A*x.^2 + B*x.*y + C*y.^2 + D*x + E*y + F
def solve_ellipse(A,B,C,D,E,F):
            
    Xc = (B*E-2*C*D)/(4*A*C-B**2)
    Yc = (B*D-2*A*E)/(4*A*C-B**2)
        
    FA1 = 2*(A*Xc**2+C*Yc**2+B*Xc*Yc-F)
    FA2 = np.sqrt((A-C)**2+B**2)
    
    MA = np.sqrt(FA1/(A+C+FA2)) #长轴
    SMA= np.sqrt(FA1/(A+C-FA2)) if A+C-FA2!=0 else 0#半长轴
    
    if B==0 and F*A<F*C:
        Theta = 0
    elif B==0 and F*A>=F*C:
        Theta = 90
    elif B!=0 and F*A<F*C:
        alpha = np.arctan((A-C)/B)*180/np.pi
        Theta = 0.5*(-90-alpha) if alpha<0 else 0.5*(90-alpha)
    else:
        alpha = np.arctan((A-C)/B)*180/np.pi
        Theta = 90+0.5*(-90-alpha) if alpha<0 else 90+0.5*(90-alpha)
            
    if MA<SMA:
        MA,SMA = SMA,MA
            
    return [Xc,Yc,MA,SMA,Theta]

Matlab代码

生成椭圆散点数据

%% parameters of the true ellipse
t = 0:1:120;
xs = 6*cosd(t);
ys = 21*sind(t);
noise = randn(2,length(xs))*0.5;
xs = xs+noise(1,:);
ys = ys+noise(2,:);
M_z = rotz(10);
M_z = M_z(1:2,1:2);
new_X = M_z*[xs; ys];
xs = new_X(1,:)+5;
ys = new_X(2,:)+4;
figure(1)
clf
scatter(xs,ys,[],'.');

拟合椭圆

X = [xs.^2;
    xs.*ys;
    ys.^2;
    xs;
    ys;
    ones(1,length(xs))];
H = zeros(6);
H(1,3)=2;
H(3,1)=2;
H(2,2)=-1;
S = X*X';

算法1：

[V,L] = eig(S,H)
L = diag(L);

绘制椭圆

for i=1:6
    if L(i)<=0
        continue;
    end
    
    W = V(:,i);
    
	if W'*H*W<0
        continue
    end
    
    W = sqrt(1/(W'*H*W))*W

    A = W(1); B = W(2); C = W(3); D = W(4); E = W(5); F = W(6); 
    funs = @(x,y) A*x.^2 + B*x.*y + C*y.^2 + D*x + E*y + F; 
    figure; 
    hold on; 
    scatter(xs,ys,[],'.'); 
    fimplicit(funs)


	Xc = (B*E-2*C*D)/(4*A*C-B^2)
	Yc = (B*D-2*A*E)/(4*A*C-B^2)

	MA = sqrt(2*(A*Xc^2+C*Yc^2+B*Xc*Yc-F)/(A+C+sqrt((A-C)^2+B^2)))
	SMA= sqrt(2*(A*Xc^2+C*Yc^2+B*Xc*Yc-F)/(A+C-sqrt((A-C)^2+B^2)))
end

Xc = 4.8793
Yc = 15.3049
MA = 3.5116
SMA = 10.5489

算法2：

[V,L] = eig(S)
E = zeros(1,6)
for i=1:size(V,2)
    E(i) = V(:,i)'*S*V(:,i);
end
E
[~,I] = min(E);
W = V(:,I)

上面是二次误差最小的二次曲线，下面是二次误差第二小的二次曲线，一个是双曲线，一个是抛物线，明显不符合要求。

因为散点只取了一小段，所以两个算法精度都很差，若是比较完整的数据，则两个算法结果差不多。

---

参考链接

一般方程求解椭圆
二次曲线判别
椭圆基础知识