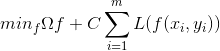SVM支持向量机-软间隔与松弛因子（3）

上一篇文章推导SMO算法时，我们通过导入松弛因子，改变了对偶问题的约束条件，这里涉及到软间隔和正则化的问题，我们一直假定训练样本是完美无缺的，样本在样本空间或特征空间一定是线性可分的，即存在一个超平面将不同类的样本完全划分开，然而现实中，数据往往不那么‘完美’，即使找到完美的它，我们也很难断定这里的线性可分是否存在过拟合。

如何解决这个问题呢，允许支持向量机在一些样本上出错，这样我们便引入了软间隔：

允许一些样本出错就是指的一些样本可能分在间隔带之内，例如A点，一个人悄悄跑到了危险边缘试探，再过分一点就是B点了，他直接跑到别人的阵营里去，而除了A，B之外，大家都安分守己，乖乖呆在自己的位置。如果我们不设定软间隔，即强行让这些点线性分开，那可能最后会得到一个训练模型精确度很高但泛化能力很差的支持向量机；这是因为个别误差大的Support Vector会对分类的超平面造成较大的影响，甚至过拟合，我们之前的硬间隔要求所有样本均满足条件，而这里软间隔则允许一些样本不满足约束。当然，在最大化间隔时，我们要求不满足约束的样本尽量少。

下面看一个目标函数：

这里我们在原优化函数的基础上，加入了损失项，即C那一部分，这里C是一个常数，又叫正则化常数，用于控制我们对犯错的容忍度，L(0/1)是0-1损失函数：

当C无穷大时，min函数会迫使所有样本满足条件，而当C取有限值时，则会允许一些样本出错。这里我是这么考虑的，C取无限大，而我们的目标函数是求min，所以我们在C很大时就会希望后面的L(0/1)函数很小，为0最好，而L(0/1)为0的条件是z≥0，即

这正是样本争取分类的条件，所以C很大时，会迫使所有样本满足，而C很小时，一些样本出错对min函数的影响很微小，从而实现软间隔。

但是有一个问题，L(0/1)函数非凸，非连续，存在间断点，数学性质不好，对目标函数优化不便，所以我们用一些其他函数代替，称为替代损失，常见的替代损失有以下几种：

动手画一下这几个函数，看看什么样子：

import math
import matplotlib.pyplot as plt
import numpy as np

def plot_loss():
	#定义x范围
	x = np.array(np.linspace(start=-2, stop=3, num=1000, dtype=np.float))
	#定义三种函数
	y_hinge = 1.0 - x
	y_hinge[y_hinge < 0] = 0
	y_logistic = np.log2(1 + np.exp(-x)) 
	y_exponential = np.exp(-x)
	#标识
	plt.plot(x, y_logistic, 'r-', label='Logistic Loss', linewidth=1)
	plt.plot(x, y_hinge, 'y-', label='Hinge Loss', linewidth=1)
	plt.plot(x, y_exponential, 'b--', label='Exponential Loss', linewidth=1)
	#图例+网格
	plt.grid()
	plt.legend()
	plt.show()
plot_loss()

可以看到，几个函数大同小异，他们都在x大于1的时候非常的小，目的就是希望我们的样本都能够大于1满足分类需求，而样本不满足，则会线性或指数形增大，从而被min函数限制，这也是损失函数的特性。

若采用Hinge损失，则优化目标变为：

引入松弛变量：

这就是常用的软间隔支持行向量机.

对于每个样本都有一个对应的松弛变量，要来表示样本不满足约束的程度，这仍是一个二次规划，下面我们引入朗格朗日乘子，求导代换求出软间隔支持向量机的对偶问题：

αi≥0，ui≥0是拉格朗日乘子,先求参数偏导：

带入原式进行化简：

从而导出对偶问题：

这里αi≤C是因为且两项都大于等于0.

类似的，通过多约束KKT条件，我们引出软间隔支持向量机的KKT条件：

基于KKT条件讨论：

1）当αi=0时，则样本分类正确，对f(x)没有影响

2）当0<αi<C时，则ui≠0,=0，yif(xi)-1+=0，所以此时的样本是支持向量

3）当αi=C时，ui=0，则≤1时，样本落在间隔带内，>1时，则样本分错类

可以看到，软间隔支持向量机与支持向量有关，而当α不满足KKT条件时，我们便对α进行更新.

拿《机器学习实战》中支持向量机的更新规则看一下是如何对不满足KKT条件定义的：

    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or 
    	((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):

上面是书中代码判断不满足KKT条件的if判断语句

先看第一句：

而对应的情况应该是αi=C，但这里and（且）的条件是αi＜C，所以不满足KKT条件，所以要对αi更新。

再看第二句：

而对应的情况应该是αi=0，但这里and（且）的条件是αi＞C，所以不满足KKT条件，所以要对αi更新。

总结：

这里我们可以把0-1损失函数替换为别的替代损失函数，从而得到其他学习模型，但他们的共性是相同的.这里的共性是指：第一项描述间隔大小，第二项描述误差：

第一项叫结构风险，用来描述模型结构的某些性质，称为正则化项，第二项叫经验风险，用来描述数据的契合度，C叫做正则化常数，用于对两者折中，类似于这样的评价函数模型的得分函数，我们在BP神经网路，Logistic回归等模型构造中，也都会遇到。有问题欢迎大家交流~

SVM支持向量机-软间隔与松弛因子（3）

猜你喜欢