SVM——线性支持向量机和软间隔最大化

1、线性支持向量机

线性可分支持向量机只适用于训练数据集线性可分的情况，而对于数据集接近线性可分的情况，利用线性可分支持向量机不可能找到一个最优分界面使得正类数据和负类数据完全分开，所以线性支持向量机这时就发挥了它的作用，它也是找到一个最优分界面，这个最优分界面允许少量的数据样本被分错，但绝大多数的样本都能够被正确分类。

假设给定特征空间上的一个训练数据集T={(x₁, y₁), (x₂, y₂), …, (x_n, y_n)}, x_i∈Rⁿ, y_i∈{-1, +1}, i=1, 2, …, N。因为数据集T不是完全线性可分的，所以存在(x_i, y_i)使得函数间隔y_i(w·x_i+b)>=1不满足，为了解决这个问题可以给每个数据样本点引入一个松弛变量ξ_i（ξ_i>=0），使得函数间隔加上松弛变量后满足大于等于1。这样一来约束条件就变成了：y_i(w·x_i+b) >= 1-ξ_i。

只有被分错的数据样本点对应的ξ_i是大于1的，位于分界面上的数据点对应的ξ_i等于1，被正确分类且位于间隔之内的数据样本点对应的ξ_i是大于0小于1的，被正确分类且位于间隔之外的数据样本点对应的ξ_i是等于0的。所以说ξ_i相当于是数据样本点(x_i, y_i)的惩罚项，根据硬间隔最大化(线性可分支持向量机)的目标表达式1/2 *||w||²得到线性支持向量机的目标函数如下：

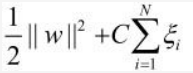
其中C>0是惩罚参数，C越大对误分类点的惩罚越大，C越小对误分类的惩罚越小。最小化线性支持向量机的目标函数包含两层含义：(1) 1/2 *||w||²越小意味着间隔越大 (2)目标表达式后面部分越小意味着误分类点数越少(因为只有被分错的数据样本点对应的ξ_i是大于1的)。所以最小化目标函数要使得间隔最大同时误分类点数最少，C是用来调和两者的系数。
可以根据训练数据集线性可分时的线性可分支持向量机思路来考虑线性不可分时的线性支持向量机问题，相对于硬间隔最大化称它为软间隔最大化。

得到线性支持向量机的原始问题：

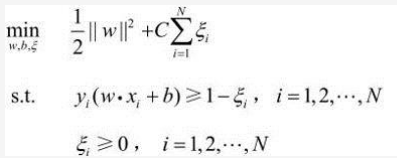
求得原始问题的最优解w^* 和b^* 就得到了最优分界面w^* ·x+b^* = 0和线性支持向量机f(x) = sign(w^*·x+b^*)。

2、求原始问题的对偶问题

原始问题的拉格朗日函数如下：

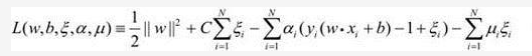
其中α_i>=0, μ_I>=0是拉格朗日乘子。
对偶问题是原始问题拉格朗日函数的极大极小问题，所以先求拉格朗日函数对w，b，ξ_i的极小化，由

得

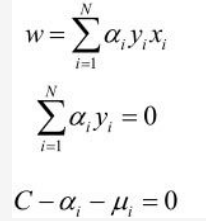
将上述结果带入拉格朗日函数中得：

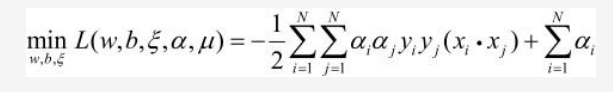
然后再对min L(w, b, ξ, α, μ)求α的极大化就得到原始问题的对偶问题如下：

因为对偶问题的表达式中没有μ_i，所以可以简化约束条件，C - α_i - μ_i =0和μ_i>=0简化为 C - α_i>=0即 α_i<=C，又因为α_i>=0，所以上述后三个约束条件最终化简为0<=α_i<=C。接着将对偶问题的表达式转换成求极小(原来是求极大)，可得最终的对偶问题如下：

3、对偶问题的最优解求原始问题的最优解

若存在w^*, b^* , ξ^*, α^* , μ^*使得w^*, b^* , ξ^* 是原始问题的最优解且α^* 是对偶问题的最优解，充分必要条件是原始问题是凸优化问题且w^*, b^* , ξ^*, α^* , μ^*满足KKT条件。
根据KKT条件可得：

对偶问题的最优解α* 可以通过SMO(序列最小最优化方法)求得，这里先不讲，假设最优解α* =（α₁* , α₂* ,…, α_N* ）。
由A可得：

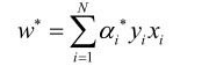
由B，因为α^*的分量中肯定存在一个0<α_j<C（由对偶问题的约束条件可得），所以对应的y_j(w^*·x_j+b^*) -1+ξ_j=0。
由C，因为u_i =C - α_i（由约束条件C - α_i - u_i =0得），又因为存在0<α_j<C，所以对应的u_j >0，所以ξ_j =0。
所以由B和C最终可得 y_j(w^*·x_j+b^*) -1 = 0，两边同乘上y_j得：b^* = y_j - w^*·x_j，再将w^*带入得：

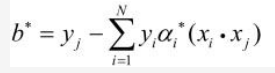
所以只要求出对偶问题的解α^*就解决了全部问题。