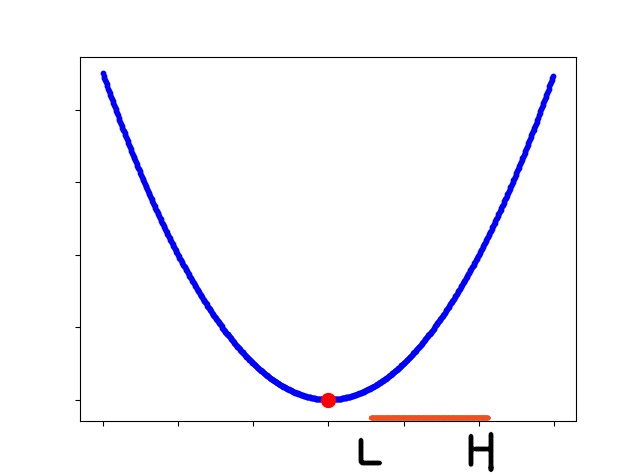
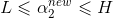SVM支持向量机-SMO算法推导(2)一文中我们写到了α2的范围选择,这里单独解释一下L,H的计算,和α2的调整规则。
1.范围限定
先看一下SMO算法推导那篇文章中α2的范围:
依据简化约束,我们需要分两种情况讨论(其实是四种),y1=y2 和 y1≠y2:
y1≠y2时:
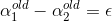
∴ L=max(0,-ε) H=min(C,C-ε)
y1=y2时:
∴ L=max(0,ε-C) H=min(C,ε)
讨论第一种情况(为了与图片一致,ε改为ζ):
y1≠y2,即y1,y2异号,此时我们假设y1=1,y2=-1,则α1-α2=ζ,这里我们需要讨论ζ的范围:
Tips:这里适当用X,Y轴代替表达,希望大家可以理解
1)当ζ > C,或ζ < -C时,直线α1-α2 = ζ,与 CxC 的方形没有交集,所以此时α2的范围为空集
2)当0 ≤ ζ ≤C时,对应Y=X下面这条直线,因为截距是-ζ,此时α1-α2=ζ,交X轴于(ζ,0),与X=C交于(C,C-ζ),对
应α2的范围是[0,C-ζ]
3)当-C ≤ ζ ≤0时,对应Y=X上面这条直线,此时α1-α2=ζ,在CxC范围内交X=0于(0,-ζ),与Y=C交于(C+ζ,C),对应α2的范围是[-ζ,C]
综上所述:
L=max(0,-ζ) H=min(C,C-ζ)
这里又ζ = α1-α2,带入到L,H中,得到α2的范围:
[ L=max(0,α2-α1) , H=min(C,C-α1+α2) ]
y1=-1,y2=1S时讨论情况类似,这里就不再推导.
讨论第二种情况:
y1 = y2,即y1,y2同号,此时我们假设y1 = 1,y2 = 1,则α1 + α2 = ζ,这里我们需要讨论ζ的范围:
1)ζ < 0时,直线与CxC的方形区域交集为空,所以范围为空集
2)0 ≤ ζ ≤ C时,即靠左下方这条直线,他的截距限制在 [0,C] 之间,此时直线交X轴于 (ζ,0) ,交 X=0 于 (0,ζ) ,对应α2 的范围是 [ 0 ,ζ ]
3)C ≤ ζ ≤ 2C时,即靠右上方这条直线,他的截距限制在 [C,2C] 之间,此时直线交 X=C 于( C, ζ-C) 交 Y=C 于 ( ζ-C , C ),对应的α2的范围是 [ ζ-C ,C ]
4)ζ > 2C时,直线与CxC的方形区域交集为空,所以范围为空集
综上所述:
L=max(0,ζ-C) H=min(C,ζ)
这里又ζ = α1+α2,带入到L,H中,得到α2的范围:
[ L=max(0,α1+α2-C) , H=min(C,α1+α2) ]
y1=-1,y2=-1S时讨论情况类似,这里就不再推导.
2.更新调整
下面讨论更新规则:

上图是文中的更新规则,再看一下我们二次规划下α2的函数:

通过带入α1,我们可以得到α2的二次项:
程序中是默认二次项大于0的,这时我们二次函数开口向下,有最小值,分三种情况讨论:
1)α2>H时,红点为α2,即全局最小值:
L到H是递减的,所以最小值取在H处
2)L≤α2≤H时:
这时L到H的区间包含全局最小,所以最小值就是α2本身
3)α2 < L时:
L到H之间函数值递增,所以最小值取在L处
总结:
这两个问题是我在编程和看SMO算法时遇到的困惑,本以为很难,所以找了资料去查了相关的知识,但其实不是太麻烦,其次关于α2二次项的讨论,这里只是简单的讨论了默认的二次型存在且大于0的理想情况,还有小于0,等于0的情况需要去学习,所以这里的讨论还不是很完整。