文章目录
一、定义
为了使二叉树的实现变得更有具体意义,我们将实现一种叫二叉搜索树(Binary Search Tree) 的数据结构,也叫二叉查找树。
二叉搜索树要求:若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值; 它的左、右子树也分别为二叉搜索树。如下图:
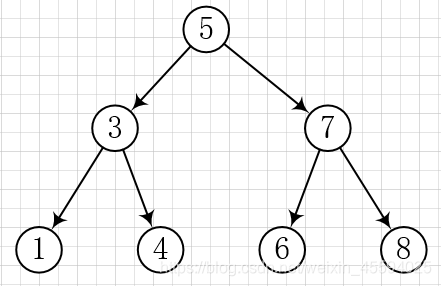
由二叉搜索树的特性看出,其结构有很强的递归性,所以二叉搜索树的很多方法都可以用递归实现,但非递归方法也要掌握,它是深入理解二叉搜索树特性的关键。
二、二叉搜索树的实现
1、二叉树的抽象数据类型
BSTADT接口声明如下:
// T表示节点元素的类型,该类型继承了Comparable接口,方便比较数据。
public interface BSTADT<T extends Comparable>{
boolean isEmpty();// 判空
void insert(T data);// 插入
T findMin();// 找最小值
T findMax();// 找最大值
BSTNode<T> findNode(T data);// 查找:查找给定数据所在的节点
int size();// 大小:二叉树的节点数
int height();// 深度:节点的最大层次
void preOrder();// 前序遍历
void infixOrder();// 中序遍历
void postOrder();// 后序遍历
void levelOrder();// 层序遍历
void remove(T data);// 删除
}2、二叉树的节点类
注:实现 Comparable 接口方便比较大小。
// 二叉搜索树节点类
public class BSTNode<T extends Comparable> {
public BSTNode<T> left;// 左孩子
public BSTNode<T> right;// 右孩子
public T data;// 数据
public BSTNode(BSTNode<T> left, BSTNode<T> right, T data) {
this.left = left;
this.right = right;
this.data = data;
}
public BSTNode(T data) {
this(null, null, data);
}
}3、插入算法的设计与实现
二叉搜索树的插入操作比较简单,我们只要利用二叉搜索树的特性(对于树中的每个节点 T,它的左子树中所有节点的值都小于 T 中的值,右子树中所有节点的值都大于 T 中的值),找到对应的插入位置即可。
如,要插入 data = 4 的节点。从根节点开始,沿着树查找(比较 data 与节点数据的大小从而决定往左子树还是右子树继续查找),如果找到 data(4),则已有数据不用再插入,否则将 data(4) 插入到遍历的路径上的最后一个节点,如下图所示:
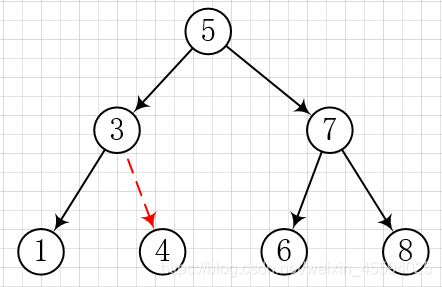
代码实现:
@Override
// 插入————递归实现
public void insert(T data) {
root = insert(data, root);
}
private BSTNode<T> insert(T data, BSTNode<T> p){
if(p == null){// 空树
p = new BSTNode<T>(null, null, data);
}
int result = data.compareTo(p.data);
if(result < 0){// 向左
p.left = insert(data, p.left);
}else if(result > 0){// 向右
p.right = insert(data, p.right);
}else{
p.data = data;// 已有元素不用再插入
}
return p;
}
// 插入————非递归实现
public boolean insertUnrecure(T data){
BSTNode<T> node = new BSTNode<>(data);
if(root == null){// 空树
root = node;
return true;
}else{
BSTNode<T> current = root;
BSTNode<T> parent = null;
while(current != null){
parent = current;
int result = data.compareTo(current.data);
if(result < 0){// 插入值比当前节点值小,搜索左子树
current = current.left;
if(current == null){
// 左子节点为空,将新值插入到该节点
parent.left = node;
return true;
}
}else if(result > 0){// 插入值比当前节点值大,搜索右子树
current = current.right;
if(current == null){
// 右子节点为空,将新值插入到该节点
parent.right = node;
return true;
}
}
}
}
return false;
}4、查找——查找最大值、最小值以及查找给定数据所在的节点
要找最小值,从根节点开始,一直找它的左孩子,直到找到没有左孩子的节点,那么这个节点就是最小值所在的节点。同理要找最大值,一直找根节点的右孩子,直到没有右孩子的节点,就是最大值所在的节点。
代码如下:
@Override
// 查找最小值————递归实现
public T findMin() {
if(isEmpty()){
return null;
}
return findMin(root).data;
}
private BSTNode<T> findMin(BSTNode<T> p){
if(p == null){// 递归结束条件
return null;
}
if(p.left == null){// 如果没有左孩子,p就是最小的
return p;
}
return findMin(p.left);
}
// 查找最小值————非递归实现
public T findMinUnrecure(BSTNode<T> p){
if(p == null){// 空树
return null;
}
while(p.left != null){
p = p.left;
}
return p.data;
}
@Override
// 查找最大值————递归实现
public T findMax() {
if(isEmpty()){
return null;
}
return findMax(root).data;
}
private BSTNode<T> findMax(BSTNode<T> p){
if(p == null){// 递归结束条件
return null;
}
if(p.right == null){// 如果没有右孩子,p就是最大的
return p;
}
return findMax(p.right);
}
// 查找最大值————非递归实现
public T findMaxUnrecure(BSTNode<T> p){
if(p == null){
return null;
}
while(p.right != null){
p = p.right;
}
return p.data;
}
@Override
// 查找给定数据所在的节点
public BSTNode<T> findNode(T data) {
BSTNode<T> node = root;
while(node != null){
int result = data.compareTo(node.data);
if(result < 0){// 搜索左子树
node = node.left;
}else if(result > 0){// 搜索右子树
node = node.right;
}else{
return node;// 找到了
}
}
return null;// 遍历完整棵树没找到,返回null
}5、计算深度(height)和大小(size)的设计与实现
(1)树的深度(height)即为树中节点的最大层次。从根结点开始,计算出左子树的深度和右子树的深度,则树的深度为:(两棵子树中深度较大值 + 1)。深度的求解过程图示如下:
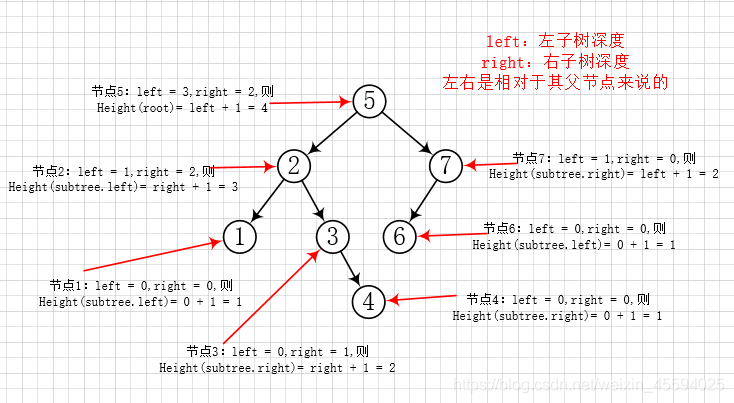
代码如下:
@Override
// 树的深度
public int height() {
return height(root);
}
private int height(BSTNode<T> subtree){
if(subtree == null){// 递归结束条件
return 0;
}
int l = height(subtree.left);// 左子树的深度
int r = height(subtree.right);// 右子树的深度
return (l > r) ? (l + 1) : (r + 1);
}(2)树的大小(size)就是树的节点数。利用递归思维,树的节点数 = 左子树的节点数 + 右子树的节点数 + 1(根节点)。代码如下:
@Override
// 树的大小(节点数)
public int size() {
return size(root);
}
private int size(BSTNode<T> subtree){
if(subtree == null){
return 0;
}
// 左子树节点数 + 右子树节点数 + 根节点
return size(subtree.left) + size(subtree.right) + 1;
}6、二叉搜索树的遍历
遍历树是根据一种特定的顺序访问树的每一个节点。比较常用的有前序遍历、中序遍历、后序遍历和层序遍历。而二叉搜索树最常用的是中序遍历(从小到大)。
(1)前序遍历:根节点——》左子树——》右子树
(2)中序遍历:左子树——》根节点——》右子树
(3)后序遍历:左子树——》右子树——》根节点
(4)层序遍历:从根节点开始,按层次向下遍历。兄弟优先访问,两个兄弟结点的访问顺序是先左后右。利用队列的特性来实现,该容器必须告诉我们下一个要访问的节点是谁,层次遍历的规则是兄弟优先,从左往右,因此在访问时,必须先将当前正在访问的节点的左右孩子依次放入容器,并且先进入的先访问。
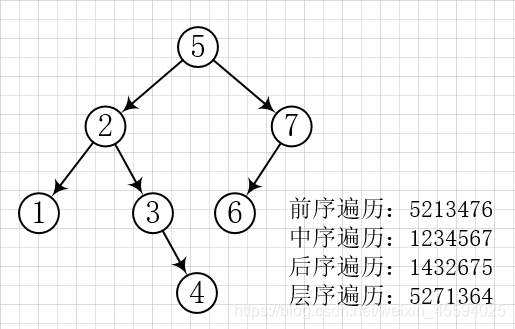
代码如下:
@Override
// 前序遍历
public void preOrder() {
System.out.print("前序遍历:");
preOrder(root);
System.out.println();
}
// 前序遍历的递归实现————根节点——》左子树——》右子树
private void preOrder(BSTNode<T> node){
if(node != null){
System.out.print(node.data + " ");
preOrder(node.left);
preOrder(node.right);
}
}
@Override
// 中序遍历
public void infixOrder() {
System.out.print("中序遍历:");
infixOrder(root);
System.out.println();
}
// 中序遍历的递归实现———左子树———》根节点——》右子树
private void infixOrder(BSTNode<T> node){
if(node != null){
infixOrder(node.left);
System.out.print(node.data + " ");
infixOrder(node.right );
}
}
@Override
// 后序遍历
public void postOrder() {
System.out.print("后序遍历:");
postOrder(root);
System.out.println();
}
// 后序遍历的递归实现———左子树———》右子树——》根节点
private void postOrder(BSTNode<T> node){
if(node != null){
postOrder(node.left);
postOrder(node.right );
System.out.print(node.data + " ");
}
}
@Override
/*
* 层序遍历:
* 利用队列的特性来实现,该容器必须告诉我们下一个要访问的节点是谁,层次遍历的规则是兄弟优先,
* 从左往右,因此在访问时,必须先将当前正在访问的节点的左右孩子依次放入容器,并且先进入的先访问
*/
public void levelOrder() {
System.out.print("层序遍历:");
BSTNode<T> node = root;
LinkedList<BSTNode<T>> list = new LinkedList<>();
list.add(node);
while(list.isEmpty()){
node = list.poll();// 遍历并移除list的头元素
System.out.print(node.data + " ");
if(node.left != null){
list.offer(node.left);// 左孩子添加到list的尾部
}
if(node.right != null){
list.offer(node.right);// 右孩子添加到list的尾部
}
}
System.out.println();
}7、删除算法的设计
二叉树的删除操作比较复杂,因为涉及到了多种情况(设要删除的节点为 current,其父节点为 parent):
(1)如果要删除的节点 current 恰好是叶节点,那么它可以立即被删除。如下图:

(2)如果要删除的节点 current 只有一个孩子,则应该调整要删除节点的父节点(parent.left 或 parent.right)指向被删除节点的孩子(current.left 或 current.right)。如下图:
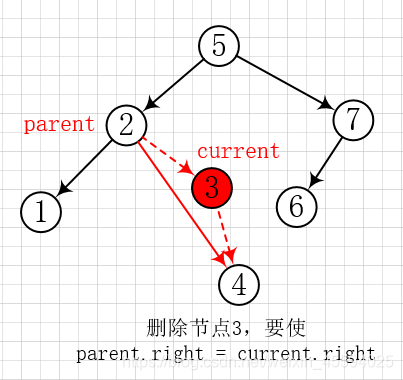
(3)如果要删除的节点 current 拥有两个孩子,则删除策略是用 current 的右子树的最小的数据替代要删除节点的数据,并递归删除用于替换的节点(此时该结点已为空)。(注意:真正要删除的节点是用于替换的那个节点)
采用这种策略的原因是右子树的最小节点的数据替换要被删除的节点后依然可以维持二叉搜索树的结构和特性(因为右子树的最小节点比右子树其它节点的数据小,比左子树所有节点的数据大),并且右子树的最小节点不可能有左孩子,删除起来也相对简单。如下图:
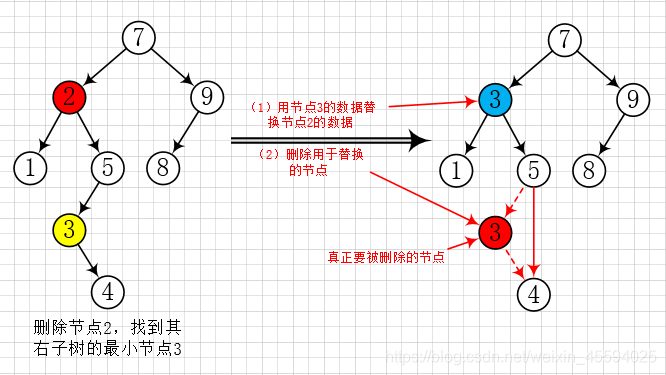
删除算法的实现(递归):
@Override
// 删除数据————递归实现
public void remove(T data) {
if(data == null){
System.out.println("要删除的数据不能为空!");
return;
}
root = remove(data, root);
}
/*
* 删除数据的递归实现,有三种情况(首先要找到要删除数据所在的节点):
* 1、删除叶节点
* 2、删除拥有一个孩子的节点(可能是左孩子也可能是右孩子)
* 3、删除拥有两个孩子的节点
*/
private BSTNode<T> remove(T data, BSTNode<T> node){
// 要删除的元素不存在,递归结束的条件
if(node == null){
return node;
}
int result = data.compareTo(node.data);
if(result < 0){// 向左递归删除
node.left = remove(data, node.left);
}else if(result > 0){// 向右递归删除
node.right = remove(data, node.right);
}else{// result = 0表示找到要删除数据所在的节点
if(node.left != null && node.right != null){// 要删除的节点有两个孩子
// (1)找到右子树中最小节点的元素并替换要删除的元素
node.data = findMin(node.right).data;
// (2)移除用于替换的节点
node.right = remove(node.data, node.right);
}else{
// 删除只有一个孩子和删除叶节点的情况
node = (node.left == null) ? node.right : node.left;
}
}
return node;
}删除算法的实现(非递归):
// 删除数据————非递归实现
public void removeUnrecure(T data){
if(data == null){
System.out.println("要删除的数据不能为空!");
return;
}
BSTNode<T> current = root;// 记录要删除的节点
BSTNode<T> parent = root;// 记录要删除的节点的父节点
boolean isLeft = true;// 判断是左孩子还是右孩子
// 1、查找要删除数据所在的节点
while(data.compareTo(current.data) != 0){
parent = current;
int result = data.compareTo(current.data);
if(result < 0){
isLeft = true;
current = current.left;
}else if(result > 0){
isLeft = false;
current = current.right;
}
// 没找到,返回
if(current == null){
return;
}
}
// 2、删除数据
if(current.left == null && current.right == null){// 删除叶节点
if(current == root){
root = null;
}else if(isLeft){
current.left = null;
}else{
current.right = null;
}
}else if(current.left == null){// 删除只有右孩子的节点
if(current == root){
root = current.right;
}else if(isLeft){// current是parent的左孩子
parent.left = current.right;
}else{// current是parent的右孩子
parent.right = current.right;
}
}else if(current.right == null){// 删除只有左孩子的节点
if(current == root){
root = current.left;
}else if(isLeft){// current是parent的左孩子
parent.left = current.left;
}else{// current是parent的右孩子
parent.right = current.left;
}
}else{// 删除有两个孩子的节点
// 找到当前要删除节点current的右子树中的最小值元素
BSTNode<T> successor = findSuccessor(current);
if(current == root){
root = successor;
}else if(isLeft){// current是parent的左孩子
parent.left = successor;
}else{// current是parent的右孩子
parent.right = successor;
}
// successor的left指向要删除节点的左孩子
successor.left = current.left;
}
}
// 查找要删除节点右子树的最小节点,用于替换要删除的节点数据,命名为中继节点,方法的参数为要删除的节点
private BSTNode<T> findSuccessor(BSTNode<T> deleteNode){
BSTNode<T> successor = deleteNode;
BSTNode<T> successorParent = deleteNode;
BSTNode<T> tempNode = deleteNode.right;
// 查找要删除节点的右子树中的最小节点,结果放在successor中
while(tempNode != null){
successorParent = successor;
successor = tempNode;
tempNode = tempNode.left;
}
/*
* 删除:
* (1)如果要删除节点的右孩子是successor,直接将successor返回remove()进行删除;
* (2)如果要删除节点的右孩子不是successor,删除操作为:
* successor的父节点的left指向successor的右孩子;
* successor替换要删除的节点,successor的right指向要删除节点的右孩子;
* successor的left和parent在remove()中处理
*/
if(successor != deleteNode.right){
successorParent.left = successor.right;
successor.right = deleteNode.right;
}
return successor;
}8、二叉树的构建与实现
已知二叉树的一种遍历顺序,不能唯一确定一棵二叉树。这是因为,前序遍历和后序遍历反映的是双亲与孩子节点之间的关系,而中序遍历反映的则是兄弟节点之间的关系。可以通过前序遍历和中序遍历序列或者后序遍历和中序遍历序列唯一确定一棵二叉树,而前序遍历和后序遍历反映的都是双亲与孩子节点的关系,所以无法唯一确定一棵二叉树。
1、由前序遍历和中序遍历序列构建二叉树
已知前序遍历序列 preList=ABDGCEFH 和中序遍历序列 infixList=DGBAECHF,确定二叉树的过程图示如下:

从图中我们可以发现,整个构建过程都是在不断递归,即将整棵树简化为子树进行分析。设数组 preList 和 infixList 分别表示一个二叉树的前序和中序遍历序列,两个序列的长度都为 n,则二叉树的构建过程如下:
(1)由前序遍历序列可知,二叉树的根节点为 preList[0],设中序遍历序列中根节点的位置为 i(0≤i≤n),则有 preList[0]=infixList[i]。
(2)再由中序遍历序列可知,infixList[i] 之前的元素为根节点的左子树,infixList[i] 之后的元素为根节点的右子树。
因此,根节点的左子树有 i 个节点,子序列如下:
- 左子树的前序遍历序列:preList[1] , … , preList[i]
- 左子树的中序遍历序列:infixList[0] ,… , infixList[i-1]
根节点的右子树有 n-i-1 个节点,子序列如下:
- 右子树的前序遍历序列:preList[i+1] , … , preList[n-1]
- 右子树的中序遍历序列:infixList[i+1] , … , infixList[n-1]
(3)循环步骤(1)、(2),即可确定二叉树。
代码如下:
// 用前序遍历序列和中序遍历序列构建二叉树,返回值为根节点
public BSTNode<T> createBSTByPreInfix(T[] preList, T[] infixList,
int preStart, int preEnd, int infixStart, int infixEnd){
// (1)前序遍历序列的第一个元素是根节点(root)
BSTNode<T> node = new BSTNode<>(preList[preStart]);
// 若数组中只有一个元素,只用构建一个根节点
if(preStart == preEnd){
return node;
}
// (2)确定根节点在中序遍历序列中的位置
int i = 0;
for (i = infixStart; i <= infixEnd; i++) {
if(preList[preStart].compareTo(infixList[i]) == 0){
break;
}
}
// (3)递归构建左子树
int leftLength = i - infixStart;// 左子树的长度
if(leftLength > 0){
// 左子树的前序遍历序列:preList[1], ... , preList[i]
// 左子树的中序遍历序列:infixList[0], ... , infixList[i - 1]
node.left = createBSTByPreInfix(preList, infixList, preStart + 1,
preStart + leftLength, infixStart, i - 1);
}
// (4)递归构建右子树
int rightLength = infixEnd - i;// 右子树的长度
if(rightLength > 0){
// 右子树的前序遍历序列:preList[i + 1], ... , preList[n - 1]
// 右子树的中序遍历序列:infixList[i + 1], ... , infixList[n - 1]
node.right = createBSTByPreInfix(preList, infixList,
preStart + leftLength + 1, preEnd, i + 1, infixEnd);
}
return node;
}2、由后序遍历和中序遍历序列构建二叉树
根据后序遍历序列和中序遍历序列,我们也可以唯一确定一棵二叉树。设后序遍历序列为GDBEHFCA,中序遍历序列为 DGBAECHF,确定二叉树的过程图示如下:
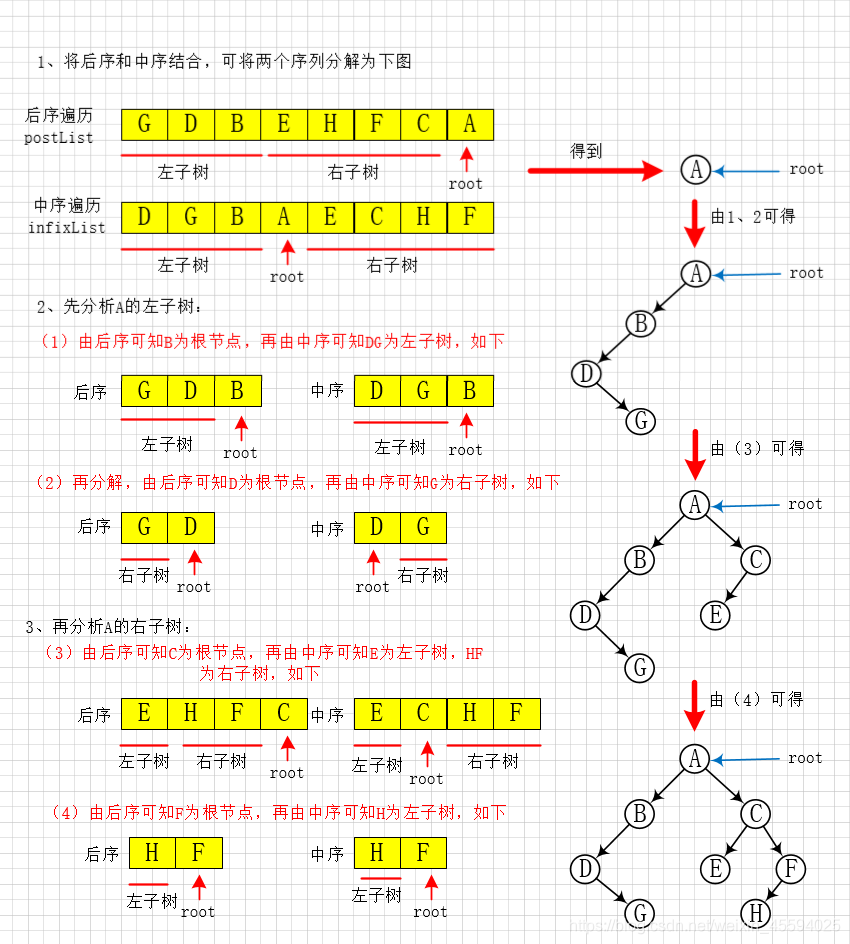
设数组 postList 和 infixList 分别表示一个二叉树的后序和中序遍历序列,两个序列的长度都为 n,则二叉树的构建过程如下:
(1)由后序遍历序列可知,二叉树的根节点为 postList[n-1],设中序遍历序列中根节点的位置为 i(0≤i≤n),则有 postList[n-1]=infixList[i] 。
(2)再由中序遍历序列可知,infixList[i] 之前的元素为根节点的左子树,infixList[i] 之后的元素为根节点的右子树。
因此,根节点的左子树有 i 个节点,子序列如下:
- 左子树的后序遍历序列:postList[0] , … , postList[i - 1]
- 左子树的中序遍历序列:infixList[0] , … , infixList[i - 1]
根节点的右子树有 n-i-1 个节点,子序列如下:
- 右子树的后序遍历序列:postList[i] , … , postList[n - 2]
- 右子树的中序遍历序列:infixList[i + 1] , … , infixList[n - 1]
(3)循环步骤(1)、(2),即可确定二叉树。
代码如下:
// 用后序遍历序列和中序遍历序列构建二叉树,返回值为根节点
public BSTNode<T> createBSTByPostInfix(T[] postList, T[] infixList,
int postStart, int postEnd, int infixStart, int infixEnd){
// (1)后序遍历序列的最后一个元素是根节点
BSTNode<T> node = new BSTNode<>(postList[postEnd]);
// 若数组中只有一个元素,只用构建一个根节点
if(postStart == postEnd){
return node;
}
// (2)确定根节点在中序遍历序列中的位置
int i = 0;
for(i = infixStart; i <= infixEnd; i++){
if(postList[postEnd].compareTo(infixList[i]) == 0){
break;
}
}
// 递归构建左子树
int leftLength = i - infixStart;// 左子树的长度
if(leftLength > 0){
// 左子树的后序遍历序列:postList[0] , ... , postList[i - 1]
// 左子树的中序遍历序列:infixList[0] , ... , infixList[i - 1]
node.left = createBSTByPostInfix(postList, infixList, postStart,
postStart + leftLength - 1, infixStart, i - 1);
}
// 递归构建右子树
int rightLength = infixEnd - i;// 右子树的长度
if(rightLength > 0){
// 右子树的后序遍历序列:postList[i] , ... , postList[n - 2]
// 右子树的中序遍历序列:infixList[i + 1] , ... , infixList[n - 1]
node.right = createBSTByPostInfix(postList, infixList,
postStart + leftLength, postEnd - 1, i + 1, infixEnd);
}
return node;
}9、测试代码
public class BSTree<T extends Comparable> implements BSTADT<T>{
private BSTNode<T> root;// 根节点
// 创建一棵空树
public BSTree(){
root = null;
}
@Override
// 判空
public boolean isEmpty() {
return root == null;
}
public static void main(String[] args) {
BSTree<Integer> tree = new BSTree<Integer>();
// 二叉树创建测试
Integer[] preList = { 7, 2, 1, 5, 3, 4, 9, 8 };
Integer[] infixList = { 1, 2, 3, 4, 5, 7, 8, 9 };
Integer[] postList = { 1, 4, 3, 5, 2, 8, 9, 7 };
int preStart = 0;
int preEnd = preList.length - 1;
int infixStart = 0;
int infixEnd = infixList.length - 1;
// 由前序和中序遍历序列创建二叉树测试
tree.root = tree.createBSTByPreInfix(preList, infixList, preStart,
preEnd, infixStart, infixEnd);
tree.postOrder();
int postStart = 0;
int postEnd = postList.length - 1;
// 由前序和中序遍历序列创建二叉树测试
tree.root = tree.createBSTByPostInfix(postList, infixList, postStart,
postEnd, infixStart, infixEnd);
tree.preOrder();
System.out.println(tree.findMin());
System.out.println(tree.findMax());
System.out.println(tree.findNode(4).data);
tree.remove(3);
tree.preOrder();
tree.infixOrder();
tree.postOrder();
}
}测试结果:
后序遍历:1 4 3 5 2 8 9 7
前序遍历:7 2 1 5 3 4 9 8
1
9
4
前序遍历:7 2 1 5 4 9 8
中序遍历:1 2 4 5 7 8 9
后序遍历:1 4 5 2 8 9 7
