动态规划（二）暴力递归的优化之路——数字三角形最大路径和

题目描述

在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可，不必给出具体路径。
三角形的行数大于1小于等于100，数字为 0 - 99

输入格式：

5      //表示三角形的行数    接下来输入三角形
7
3   8
8   1   0
2   7   4   4
4   5   2   6   5

要求输出最大和

分析

从顶点开始，求最大和。每个点都有两种选择，左下还是右下，左下和右下哪个大不知道，我们可以把下面两个点看做是新的三角形，分别求出左下三角形和右下三角形的最大路径和，那么只需选择其中较大的即可加到当前顶点即可。这是一个递归过程。

f(int[] arr,int i,int j){
  return arr[i][j]+max(f(arr,i+1,j),f(arr,i+1,j+1));
}

这份伪代码未考虑递归的出口，出口就在最后一行，因为这个时候i和j都没有办法再增加，这时该顶点相当于没有继续往下走的走法，加号后面的部分略去即可。

递归代码

  /**
   * 
   * @param triangle
   *          数字三角形
   * @param i
   *          起点行号
   * @param j
   *          起点列号
   * @return 计算出的最大和
   */
  public static int maxSumUsingRecursive(int[][] triangle, int i, int j) {
    int rowIndex = triangle.length;
    if (i == rowIndex - 1) {
      return triangle[i][j];
    } else {
      return triangle[i][j]
          + Math.max(maxSumUsingRecursive(triangle, i + 1, j),
              maxSumUsingRecursive(triangle, i + 1, j + 1));
    }
  }

对于如上这段递归的代码，当我提交到POJ时，会显示如下结果：

对的，代码运行超时了，为什么会超时呢？答案很简单，因为我们重复计算了。每个顶点左下和右下是想象的两个三角形，这两个三角形有重叠。当我们在进行递归时，计算机帮我们计算的过程如下图：

优化1：记忆型递归

就拿第三行数字1来说，当我们计算从第2行的数字3开始的MaxSum时会计算出从1开始的MaxSum，当我们计算从第二行的数字8开始的MaxSum的时候又会计算一次从1开始的MaxSum，也就是说有重复计算。这样就浪费了大量的时间。也就是说如果采用递规的方法，深度遍历每条路径，存在大量重复计算。则时间复杂度为 2的n次方,对于 n = 100 行，肯定超时。

接下来，我们就要考虑如何进行改进，改进的思路是：考察递归中变化且可以表示递归过程的参数，本例中是两个，代表行号和列号。我们可以把计算过的(i,j)位置的结果缓存起来，下次直接拿来使用。

有两个参数，缓存数组也就是二维的。

根据这个思路，我们就可以将上面的代码进行改进，使之成为记忆递归型的动态规划程序：

  /**
   * 记忆型递归
   * @param triangle
   * @param i
   * @param j
   * @return
   */
  public static int maxSumUsingMemory(int[][] triangle, int i, int j, int[][] map) {
    int rowIndex = triangle.length;
    int value = triangle[i][j];
    if (i == rowIndex - 1) {
    } else {
      //缓存有值，便不递归
      int v1 = map[i + 1][j];
      if (v1 == 0) {
        v1 = maxSumUsingMemory(triangle, i + 1, j,map);
      }
      //缓存有值，便不递归
      int v2 = map[i + 1][j+1];
      if (v2 == 0) {
        v2 = maxSumUsingMemory(triangle, i + 1, j+1,map);
      }
      value = value
          + Math.max(v1, v2);
    }
    //放入缓存
    map[i][j]=value;
    return value;
  }

时间复杂度为N²，空间复杂度为N²。

递推

接下来观察在存放map缓存值时，一个具体的值是通过哪些位置的值求出的。本例中得出i，j位置的最大值需要先计算i + 1, j位置和i + 1, j+1位置。

那么动态规划就是精确定义计算顺序，先求出被依赖的位置。鉴于i最多到数组的最后一行，我们可以从最后一行开始计算，然后计算倒数第二行，以此类推。让我们一步一步来完成这个过程。
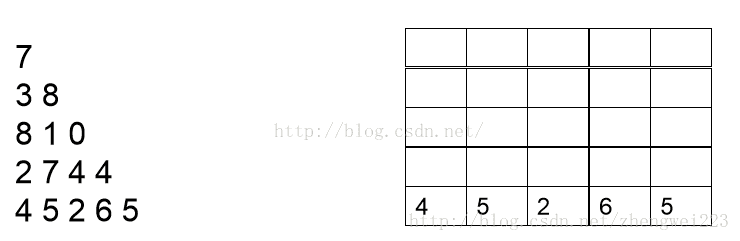
我们首先需要计算的是最后一行，因此可以把最后一行直接写出，如下图：

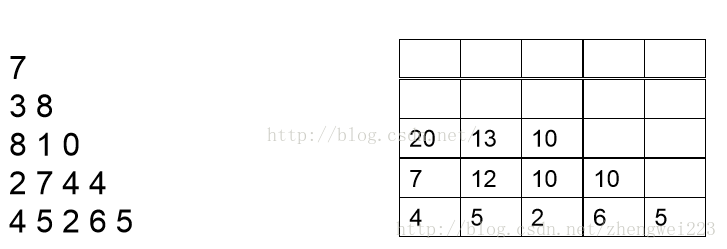
现在开始分析倒数第二行的每一个数，现分析数字2，2可以和最后一行4相加，也可以和最后一行的5相加，但是很显然和5相加要更大一点，结果为7，我们此时就可以将7保存起来，然后分析数字7，7可以和最后一行的5相加，也可以和最后一行的2相加，很显然和5相加更大，结果为12，因此我们将12保存起来。以此类推。。我们可以得到下面这张图：

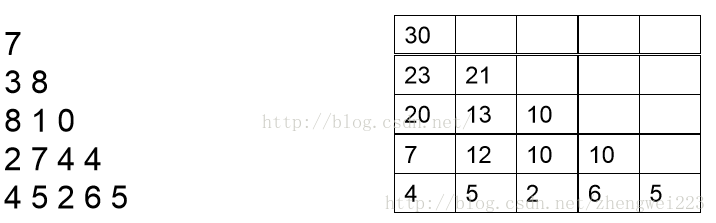
然后按同样的道理分析倒数第三行和倒数第四行，最后分析第一行，我们可以依次得到如下结果：

显然，我们可以采用二维动态规划表，但对于不需要精确路径的题目，我们可以压缩空间，使用一维数组反复利用即可，具体见代码：

  public static int maxSumUsingDp(int[][] triangle, int i, int j) {
    int rowCount = triangle.length;
    int columnCount = triangle[rowCount-1].length;
    int[] states = new int[columnCount];
    for (int k = 0; k < columnCount; k++) {
      states[k] = triangle[rowCount-1][k];
    }
    for (int row = rowCount-2; row >= 0; row--) {
      for (int col = 0; col < triangle[row].length; col++) {
        states[col] = triangle[row][col]+Math.max(states[col], states[col+1]);
      }
    }
    return states[0];
  }

总结

接下来，我们就进行一下总结：

递归到动规的一般转化方法：

递归函数有n个变化的参数，就定义一个n维的数组，数组大小是参数的取值范围，数组的下标代表参数取值的组合，称为状态，元素的值是该状态的值。

如果这些状态会被反复计算，就可以建立一个辅助数组来存储计算过的值，在需要某状态的值时，先查辅助数组，这样可以减少计算次数。

作为递归的逆过程，考虑辅助数组的缓存值的形成。递归是层层依赖，动规则是定义计算顺序先计算被依赖的值。从边界值开始， 逐步填充数组。

背包问题是2维数组，物品个数*背包重量

钢条问题是2维数组，切割方式*长度

本例问题是二维数组，i*j

这些问题都可以遵循递归-记忆型递归-动态规划的优化之路。