机器学习基础（一）：支持向量机原理

一、前言

支持向量机（Support Vectore Machine，SVM）学习问题可以表示为凸优化问题，能够在小样本训练量的情况下，使用有效地算法求解线性及非线性问题的全局最优解。支持向量机在求解非线性分类问题时，利用核技巧将非线性问题从低维空间向高维空间映射，然后采取线性分类问题的方式去解决。在非线性问题上的优异表现及较高的鲁棒性，使得支持向量机成功应用于语音识别、人脸识别、图像处理等领域。

二、基础

1.概念

支持向量机以间隔最大化为目标，采取硬间隔最大化（Hard margin）与软间隔最大化（Soft margin）的模型，寻找一个超平面对样本进行分割。支持向量机三个核心要点为间隔、对偶、核技巧。
1）训练样本线性可分时，采用硬间隔最大化训练线性可分支持向量机；
2）训练样本近似线性可分时，采用软间隔最大化训练线性支持向量机；
3）训练样本非线性时，基于核技巧，采用硬间隔最大化或软间隔最大化训练非线性支持向量机。

在样本空间中，划分超平面可通过如下线性方程来描述：
$\omega^\tau x_i+b=0$

其中 $w$为法向量，决定了超平面的方向， $b$为位移量，决定了超平面与原点的距离。

假设超平面能将训练样本正确地分类，即对于训练样本 $(xi,yi)$，满足以下公式：
$\left\{\begin{array}{l}\omega^\tau x_i+b>0,y_i=+1\\\omega^\tau x_i+b<0,y_i=-1\end{array}\right.$
其中， $y_i=+1$ 表示样本为正样本， $y_i=-1$表示样本为负样本。

2.函数间隔与几何间隔

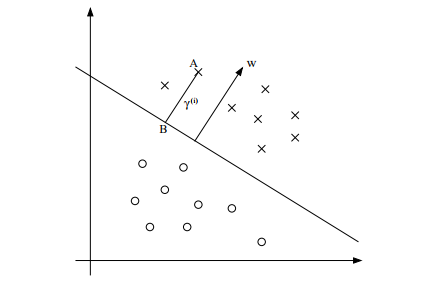
由超平面的公式可得知超平面 $(\omega,b)$关于样本 $(x_i,y_i)$的函数间隔为：
${\widehat\gamma}_i=y_i\left(\omega^\tau x_i+b\right)$

如果成比例地改变 $\omega$和 $b$，超平面没有改变，函数间隔却有所变化。函数间隔可以表示分类预测的正确性及确信度，但是不足以选择分离超平面，因此引出超平面 $(\omega,b)$关于样本 $(x_i,y_i)$的几何间隔，即样本点至超平面的距离：
${\gamma}_i=y_i\left(\frac{\omega^\tau}{\left\|\omega\right\|}x_i+\frac b{\left\|\omega\right\|}\right)$

即使超平面参数 $\omega$和 $b$成比例地改变，几何间隔也不会变化。

三、硬间隔最大化

1.间隔最大化

下面考虑如何求得一个几何间隔最大的分离超平面，即最大间隔分离超平面。该问题可以表示为下面的约束最优化问题：
$\left\{\begin{array}{l}\underset{\omega,b}{max}\;\;\;\gamma\\s.t.\;\;\;\;y_i\left(\frac{\omega^\tau}{\left\|\omega\right\|}x_i+\frac b{\left\|\omega\right\|}\right)\geq\gamma,\;\;\;\;\;i=1,2,...,N\end{array}\right.$

该优化问题可改写为：
$\left\{\begin{array}{l}\underset{\omega,b}{max}\;\;\;{\textstyle\frac{\widehat\gamma}{\left\|\omega\right\|}}\\s.t.\;\;\;\;y_i\left(\omega^\tau x_i+b\right)\geq\gamma,\;\;\;\;\;i=1,2,...,N\end{array}\right.$

由于函数间隔 $\widehat\gamma$可随着 $\omega$和 $b$等比例缩放，它的取值不影响最优化问题的求解，因此取 $\widehat\gamma=1$，注意到求最大化 $\frac1{\left\|\omega\right\|}$和最小化 $\frac12\left\|\omega\right\|^2$是等价的，于是得到下面的线性可分支持向量机学习的最优化问题：
$\left\{\begin{array}{l}\underset{\omega,b}{min}\;\;\;{\textstyle\frac12\left\|\omega\right\|^2}\\s.t.\;\;\;\;y_i\left(\omega^\tau x_i+b\right)\geq1,\;\;\;\;\;i=1,2,...,N\end{array}\right.$

这是一个凸二次规划问题（QP问题）及原问题，即可对问题进行求解。

由最优化问题的约束条件得到下面对于训练样本 $(xi,yi)$满足的公式，也是我们常见的约束条件：
$\left\{\begin{array}{l}\omega^\tau x_i+b\geq1,y_i=+1\\\omega^\tau x_i+b\leq1,y_i=-1\end{array}\right.$

2.对偶算法

我们要求解的是最小化问题，可以构造一个可行解区域内与原目标函数完全一致的函数，而在可行解区域外的数值非常大，甚至是无穷大，那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。因此基于拉格朗日乘子法将约束条件放到目标函数中，将有约束的优化问题转换为无约束问题。然后利用凸优化问题的强对偶性，对问题再进行一次转换，最终实现问题的求解。也正是基于对偶算法，SVM才能应用核函数去解决非线性的问题。

1）构造拉格朗日目标函数

拉格朗日目标函数
$L(\omega,b,\alpha)=\frac12\left\|\omega\right\|^2+\sum_{i=1}^N\alpha_i\left[1-y_i\left(\omega^\tau x_i+b\right)\right]$

其中 $\alpha_i$是拉格朗日乘子， $\alpha_i\geq0$。原问题即可转化为新的目标函数：
$\underset{\omega,b}{min}\;\;\underset{\alpha_i\geq0}{max}\;\;L(\omega,b,\alpha)$

2）强对偶性

基于凸优化问题具有强对偶性的特点，使用拉格朗日函数对偶性，将最小和最大的位置交换一下，形成新的优化目标函数：
$\underset{\alpha_i\geq0}{max}\;\;\underset{\omega,b}{min}\;\;L(\omega,b,\alpha)$

3）求解

求 $L(\omega,b,\alpha)$关于 $\omega$和 $b$的极小值，我们分别对 $\omega$和 $b$偏导数，令其等于0，即：
$\frac{\partial L}{\partial\omega}=0\Rightarrow\omega^\ast=\sum_{i=1}^Na_iy_ix_i\\\frac{\partial L}{\partial b}=0\Rightarrow\sum_{i=1}^Na_iy_i=0$

将结果带入 $L(\omega,b,\alpha)$，可得：
$\underset{w,b}{min}L\left(\omega,b,a\right)=-\frac12\sum_{i=1}^N\sum_{j=1}^Na_ia_jy_iy_jx_i^Tx_j+\sum_{i=1}^Na_i$

因此原问题经过强对偶转化后得到的目标函数为：
$\underset a{max}-\frac12\sum_{i=1}^N\sum_{j=1}^Na_ia_jy_iy_jx_i^Tx_j+\sum_{i=1}^Na_i\\s.t.\;\;a_i\geq0,\;i=1,2,...,n\\\;\;\;\;\;\;\;\sum_{i=1}^Na_iy_i=0$

该问题可直接求解 $\alpha$，也可以使用高效的序列最小优化（SMO）算法求解 $\alpha$，然后求解 $\omega$和 $b$。其中 $\omega$的公式已经求出，而 $b$可基于以下的KKT条件进行推导求解。

3.KKT条件

一个最优化模型能够表示成下列的标准形式：
$\left\{\begin{array}{l}min\;f\left(x\right)\\s.t.\;\;g_j\left(x\right)\leq0,\;j=1,2,...,m\\\;\;\;\;\;\;\;h_k\left(x\right)=0,\;k=1,2,...,l\end{array}\right.$

该优化模型需满足以下KKT（Karush-Kuhn-Tucker）条件：
1）条件一：经拉格朗日函数转化得到的目标函数 $L(\omega,b,\alpha)$对x求导为零：
2）条件二： $\alpha\cdot g_j\left(x\right)=0$；
3）条件三： $h_k\left(x\right)=0$ 。

对于经过强对偶转换后的优化问题满足：
$$\left{\begin{array}{l}\frac{\partial L}{\partial x}=0\\alpha_i\left[1-y_i\left(\omega^\tau x_i+b\right)\right]=0\1-y_i\left(\omega^\tau x_i+b\right)\leq0\\alpha_i\geq0\end{array}\right.\$$

根据支持向量机的特点，存在使得 $\alpha_i\geq0$的位于间隔边界上的样本 $(x_i,y_i)$，因此有：
$1-y_k\left(\omega^\tau x_k+b\right)=0\Rightarrow y_k\left(\omega^\tau x_k+b\right)=1\\\Rightarrow\omega^\tau x_k+b=y_k\Rightarrow b^\ast=y_k-\omega^\tau x_k$
带入 $\omega^\ast=\sum_{i=1}^Na_iy_ix_i$有：
$\left\{\begin{array}{l}\omega^\ast=\sum_{i=1}^Na_iy_ix_i\\b^\ast=y_k-\sum_{i=1}^Na_iy_ix_i^Tx_k\end{array}\right.$
然后就能求解出对偶问题的求解 $\omega$和 $b$。

四、软间隔最大化

1.间隔最大化

对于近似线性可分的问题，软间隔最大化允许存在一点点错误，因此在目标函数在硬间隔最大化的基础上增加损失函数。
求解 $\underset{\omega,b}{min}\;\;\;{\textstyle\frac12\left\|\omega\right\|^2}$的问题变为 $\underset{\omega,b}{min}\;\;\;{\textstyle\frac12\left\|\omega\right\|^2+loss}$的问题。

2.合页损失函数

期望 $y_i\left(\omega^\tau x_i+b\right)\geq1$时， $loss$为0； $y_i\left(\omega^\tau x_i+b\right)<1$时允许 $loss$存在，定义 $loss=1-y_i\left(\omega^\tau x_i+b\right)$。则合页损失函数（Hinge loss）表达式为：
$L=max\{0,1-y\left(\omega^\tau x+b\right)\}$

因此，期望求解的目标函数为：
$\underset{\omega,b}{min}\;\;\;{\textstyle\frac12\left\|\omega\right\|^2}+C\sum_{i=1}^Nmax\{0,1-y_i\left(\omega^\tau x_i+b\right)\}$

引入 $\zeta_i=1-y_i\left(\omega^\tau x_i+b\right),\;\zeta_i\geq0$，软间隔最大化的最优化问题可表示为：
$\left\{\begin{array}{l}\underset{\omega,b}{min}\;\;\;{\textstyle\frac12\left\|\omega\right\|^2}+C\sum_{i=1}^N\varsigma_i\\s.t.\;\;\;\;y_i\left(\omega^\tau x_i+b\right)\geq1-\varsigma_i,\;\;\varsigma_i\;\geq0\end{array}\right.$

五、总结

本文介绍了支持向量机的基本概念，然后以函数间隔及几何间隔为基础推导出硬间隔和软间隔最大化的原问题。以采取硬间隔最大化的线性可分支持向量机为主线，从原问题推导出对偶问题，并基于KKT条件对超平面参数进行求解。

参考资料
[1]:机器学习-白板推导系列(六)-支持向量机SVM
[2]:支持向量机——线性可分支持向量机
[3]:支持向量机原理篇之手撕线性SVM
[4]:合页损失函数的理解