3月10日 QR分解求非齐次线性，SVD分解求齐次线性最小二乘

0.0 看到一个讨论：跨学科不同思考角度

最小二乘准确来说是损失函数，梯度下降是优化方法。
线性最小二乘的超定方程通常可以通过一步解法、SVD分解来求解；
非线性的最小二乘可以通过牛顿高斯迭代、LM算法、梯度下降求解。

1.0 齐次线性方程组的解、SVD、线性最小二乘法

链接：https://blog.csdn.net/DSbatigol/article/details/9625211

1.1 齐次线性方程组

AX=0
在非齐次方程组中，A到底有没有解析解，由增广矩阵来判断：
(r(A | b) =r(A | 0)=r(A) )

r(A)=未知数个数n（约束较强）
1.A是方阵
由克莱姆法则可知：
如果A是n*n的方阵而且r（A）=n，那么该方程组有唯一的零解。
2.A不是方阵，A是m×n的(m>n)
由另一个定理：齐次线性方程解空间维数 = n - r(A) 可知，该解空间维数为0, 也就是说该解空间只含有零向量。

1.1.1.2 r(A)<未知数个数n（约束不够）
这里A是不是方阵已经无所谓了，也没有什么法则可以用，就只分成一种情况。
由齐次线性方程组解空间维数 = n - r(A) >0，所以该齐次线性方程组有非零解，而且不唯一（自由度为 n - r(A))。

1.1.2 非齐次线性方程组

AX=b

在非齐次方程组中，A到底有没有解析解，可以由增广矩阵来判断：
r(A)<r(A | b) 方程组无解；
r(A)=r(A | b) =n，方程组有唯一解；
r(A)=r(A | b) <n，方程组无穷解；
r(A)>r(A | b) 不可能，因为增广矩阵的秩大于等于系数矩阵的秩（在矩阵中加入一列，其秩只可能增大，不可能变小）。

1.2 SVD

扫描二维码关注公众号，回复： 10025788 查看本文章

1.2.1 在matlab的用法：

1. [V D] =eig(A’*A);D为A’*A的特征值对角矩阵，V为对应的特征向量。找到最小特征值对应的V中的特征向量即为最小二乘解。
2. 使用SVD分解矩阵A，[U S V] = svd(A); U 由 A*A’的特征向量组成，V 由 A’*A的特征向量组成，因此，奇异值矩阵S中最小的奇异值对应的V中的奇异向量即为最小二乘解。

1.2.2 MATLAB中a./b与a/b的区别以及左除和右除

a/b相当于a乘b的逆
a./b是a的每个元素与b的每个元素对应相除
A\B : 表示inv(A)B 解Ax=B
B/A:表示Binv(A) 解xA=B

• 应用举例：对于超定方程（非齐次线性方程的一种）的最小二乘解的情况。A*X =b。在matlab中使用一个左除命令（matlab：A\b）就可以得到最小二乘意义下的解。这个解没有模制的限制，就是实际的解。

1.3线性最小二乘法——齐次/非齐次

1.4 非齐次线性最小二乘：采用Vertical distance，竖直距离

直线拟合。这里(ATA)-1被称为A的伪逆。因为根据可逆性质，可逆矩阵一定为方阵，而这里A并不是为方阵。所以称为A的伪逆。

非齐次线性方程组不同情况下的解：欠定、适定、超定。

当 A的秩等于r 小于n，因此 在之前的例子 n是2 ，2列 ，因此 如果秩小于2 ，那么我们只有一个点 ，因此 ，该问题的答案是 取A得逆 ， 然后 将所有可能的线性解加上A的零空间 因此此问题有许多的答案

当A的秩等于n时 在之前的线性拟合的例子中 A的秩为2 （这）说明了A的许多不同行 不同点 但是 他们确实拟合于同一直线 而确切的答案是 仅仅是A的逆乘以b

当A的秩大于n，通过伪逆来求解 在MATLAB中这非常简单 就是A\b 而其为我们计算了伪逆

1.4.1 超定方程组非齐次线性最小二乘解

https://www.cnblogs.com/monoSLAM/p/5252917.html

举例： ${a_1}{x_1}+{a_2}{x_2}+{a_3}{x_3}=b$，其中 $({a_1},{a_2},{a_3},b)$为测量已知量， $({x_1},{x_2},{x_3})$为待求量。
那么只需要三组 $({a_1},{a_2},{a_3},b)$就可以求出 $({x_1},{x_2},{x_3})$。实际情况是某次实验不止测了三组数据——超定方程组，需要采用最小二乘。

a，如何转化为最小二乘形式：
例子：y = ax+b，已知（x,y）求（a,b）？
标准化：

带入测量数据：

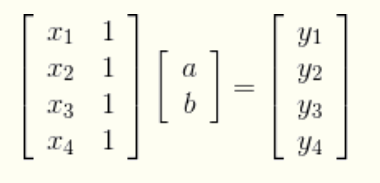
例1： $y=ax+b{x^2}$，已知 $(x,{x^2},y)$，求 $（a,b）$？
转化为标准形式：

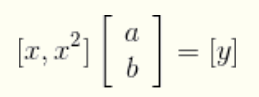
带入测量数据：

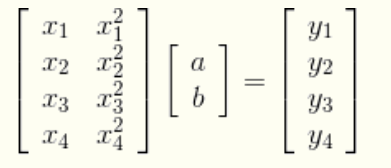
例2：

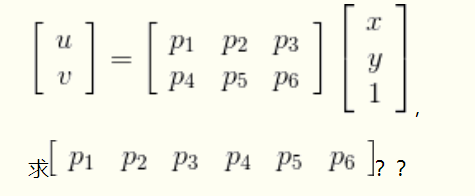
转化为标准形式：

带入测量数据：

总结：对于线性表达式，通过适当的变型即可。

在例1中，通过选取x和x^2为基实现了线性化。
对于非线性表达式，可以通过合适的基、变型，有时候也可以转化为标准形式，如例1、例2。

b， 标准形式下最小二乘的求解：
对于（1）式，最小二乘的求解，相当于求解正规方程：
${A^T}AX={A^T}B$

标准形式下最小二乘解为：
$X={\left({{A^T}A}\right)^{-1}}{A^T}B$

图源：https://blog.csdn.net/u013802188/article/details/40181601

理论上，有正规方程组可以得到线性最小二乘问题的精确解，但是由于正规方程组会出现条件数平方效应（叉积矩阵的条件数是原矩阵条件数的平方），所以往往得不到所期待的效果。https://blog.csdn.net/LCCFlccf/article/details/84875534

用QR分解求非齐次线性最小二乘法的最优闭式解

参考：https://blog.csdn.net/LCCFlccf/article/details/84875534
参考：https://blog.csdn.net/qq_29721419/article/details/69676770

QR分解法是目前求一般矩阵全部特征值的最有效并广泛应用的方法，一般矩阵先经过正交相似变化成为Hessenberg矩阵，然后再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法，与此正规正交矩阵的通用符号Q有关。可以巧妙的绕过了条件数被平方的操作

1.5齐次线性最小二乘，采用：Perpendicular distance 垂直距离

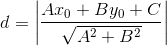
a、齐次线性最小二乘的标准形式：

AX = 0

其中A为测量数据构成的矩阵与向量，X为待求参数向量。

这里主要针对方程数多于未知元素的情形–超定方程组。

b、齐次方程组的最小二乘解的约束

因平凡解 X = 0不是我们感兴趣的解，因此我们主要是寻求该方程组的非零解。

注意，如果 X 是这个方程组的解，那么对于任何标量k，使得kX也是解，因此可以建立一个合理的约束：||X||=1的解：

齐次最小二乘相当于求解：
$min||AX|| 且 ||X||=1$
或者求解:
$min\frac{||AX||^2}{||X||}$

c、齐次方程组的最小二乘解——SVD分解得到“解”
通过前面a、b两部分的说明，此时问题的标准形式为：求使||AX||最小化并满足||X|| = 1时的X。其结论为：
$A^TA$最小特征值对应的特征向量即为待求解

SVD分解——齐次线性最小二乘

对A矩阵SVD分解:
$A=UDV^T$
那么问题变成：
$min||UDV^TX|| 且 ||X||=1$

由于：
$min||UDV^TX|| = min||DV^TX||$
即U矩阵不影响范数。

同时
$||X||=||V^TX||$
和U矩阵一样，V矩阵不影响范数。

则有：
$min||DV^TX|| 且 ||V^TX||=1$

令 ||y|| = 1，
$min||Dy|| 且 ||y||=1$

由SVD分解的规则可知，D是对角元素按降序排列的一个对角矩阵，因此该问题的解是：
$y=(0,0,0...0,1)^T$
它具有一个非零元素1并在最后的位置上。

$X=||V^Ty|| 就是V的最后一列。$

齐次下的直线拟合。注意最后方程组的解是V的最后一列。但SVD分解直接中得到的是VT，因此对应也就是VT的最后一行。

只有通过矩阵A计算奇异值U D V的转置 行向量之间相互正交

取VT的最后一行 或者V的最后一列
那便是我们用来最小化ax等于0的向量

齐次线性方程组不同情况下的解：欠定、适定、超定。

1.5.2 带约束方程组的最小二乘解

$min||AX|| 且 ||X||=1 且||CX=0||(公式一)$

求解算法总结：

a、通过对C进行SVD分解，求出 $C=UDV^T$ 。（如果C的行数少于列数，则在C矩阵的后面添加若干行0从而扩展成方阵）
b、如果对角矩阵D有r个非零对角元素，此时C的秩为 r 且C的行空间由 $V^T$的前 r 行生成。
c、C的行空间的正交补 ${C^\bot}$由余下的行生成，记 ${C^\bot}$为V的消去前 r 列得到的矩阵
d、则 $C{C^\bot}=0$，对比 $CX=0$，可以得到：
X的解由 ${C^\bot}$的列生成，把所有满足这一条件的 X 记为： $X={C^\bot}{X'}$。

由于 ${C^\bot}$的列具有正交性，因此： $||X||=||{C^\bot}{X'}||=||{X'}||$

此时，公式一 变成：

$\min||A{C^\bot}{X'}|| 且|{X'}||=1$

1.6 非线性最小二乘

非线性的最小二乘可以通过牛顿高斯迭代、LM算法、梯度下降求解。
参考：https://blog.csdn.net/tina_ttl/article/details/56833251
参考：https://www.jianshu.com/p/bf6ec56e26bd