3月20 Bundle Adjustment光束平差法概述

• 主要是参考 https://www.coursera.org/learn/robotics-perception/home/welcome 第4周里头的内容。
• 文献 “SBA: A Software Package for Generic Sparse Bundle Adjustment”， MATLAB R2016a自带的bundleAdjustment函数中都参考了这篇文献。

通常在每个基于feature的3D场景重建算法中都要用到Bundle Adjustment，作为每个基于特征的多视重建视觉算法的最后一步，它是基于3D结构和视角参数（即相机位置，朝向，固有标定和径向畸变）的优化问题，用来获得最佳的三维结构和运动（如相机矩阵）参数估计。提供初始估计，BA同时精化运动和结构参数，通过最小化观测和预测的图像点之间的投影误差。

https://www.bbsmax.com/A/E35pbvjYzv/

robotics-perception

重投影误差&调整优化的变量

一切都从两个基本问题出发：我在哪？某个点在3D坐标系的位置是什么？

由于估计的投影矩阵P有误差，进而导致投影回到像平面的点m和我们观测的m~点坐标有差异，这个差异e可以理解为重投影误差，也就是我们需要尽可能减小的。

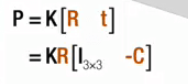
这里C是相机光心在世界坐标系中的坐标，X为该点在世界坐标系中的坐标，R为相机姿态。这三个橙色的字母就是我们需要调整优化的变量。

对于某个点，重投影误差可以如上图所示。x_、y是我们在影像上的观测坐标，u、v、w则是根据估计的相机位姿(重投影)算出来的该点坐标。这个式子中最复杂的也就是后半部分，也正是因为它导致了整个式子的非线性。更具体来说u、v、w的计算是非线性的，而u/w、v/w又是非线性的。为了后续方便，不妨将u、v、w写成关于R、C、X的函数形式，如第二行。进一步，旋转R可以参数化表达为四元数，可以写成第三行。以非线性最小二乘的形式可以看成b-f(R,C,X)的形式，如第四行。

标准的非线性最小二乘问题

一个标准的非线性最小二乘问题如上图所示，主要分为两步。首先计算误差函数的导数，并让其为0。第二步是对函数进行泰勒展开。这里Δx的式子叫做normal equation，通过求解这个式子就可以获得Δx进而可以不断迭代，是非常重要的式子。可以看到normal equation包含两个内容，一个是雅可比矩阵J，一个是负的error function。

某种程度上来说，求解normal equation就是求解雅可比矩阵J，求解出了雅可比矩阵J就可以得到normal equation，得到normal equation就可以得到Δx进而不断迭代。这里的J是雅可比矩阵，是一个m行n列的矩阵。对于每一个自变量x都有一列与其对应，对于每一个约束，都有一列与其对应。对于第i列，其元素是各个f对xi的偏导，对于第j行，每个元素是fj对于每个自变量的偏导。更直白地说，雅可比矩阵的行数代表观测个数，列数表示每次观测的变量的个数。

重投影误差的f(x)

回到我们的重投影误差问题。正如刚刚说的雅可比矩阵的求法，是要对f(x)求偏导的，因此需要写出f(x)明确的形式。在这里f(x)是由u、v、w组成的，进一步将其写成关于自变量R、C、X的形式，便于后续求偏导。

雅可比矩阵J

有了f(x)，下一步的关键问题就是雅可比矩阵J该怎么求。正如上面提到的雅可比矩阵的特性，雅可比矩阵的每一列与我们正在搜寻的未知变量有关，每一列表示对一个变量的偏导，列数等于变量个数，而f(x)又是关于R、C、X的变量，所以不妨将雅可比矩阵J拆分成R、C、X三部分。同时别忘了我们用四元数表示R，这样根据求导的链式法则就可以获得J的三部分q、C、X，q是四元数，包含4个变量，C和X都是三维坐标，包含3个变量，因此J总共包含4+3+3=10列。而我们在影像上的观测是x_、y，有两个变量，因此J的行数为2。

因此我们可以依次获得各部分的矩阵，最后组成一个完整的雅可比矩阵J。对于一个点，可以获得一个2行10列的雅可比矩阵。而对于n个点，可以以此类推获得2n行10列的大的矩阵。

多帧的情况

但上面所说针对的是一个影像中的一个点的情况，对于多帧的情况就会有所不同。可以按照上图中的形式拼接多个不同帧的雅可比矩阵。因为各帧之间的观测并不会互相干扰，因此空白部分全部为0。对于某个在两帧中都观测到的点，每一帧中的雅可比矩阵是2行17列，拼起来就是4行17列的大的矩阵。

BA的过程

简单的框架

1.特征匹配

2.RANSAC

3. 本征矩阵E矩阵计算

4. 相对平移变换

5. 三角化

6. 新相机

7. BA

中不同的三维点和相机参数相互之间影响较小，呈现一种稀疏的块结构（如图）。

用途

三维重建的最后一步是光束平差，又称bundle adjustment

整个 bundle adjustment 的目标是重投影误差最小，所以可以分为两个部分：

1，将某个误差函数的值最小化。这是一个最优化问题，用的是L-M算法。

2，将重投影误差的误差函数的具体表达式写出来，套到上面的L-M算法里头去。

输入：

• 给出从不同视角拍摄的，描述同一个场景的一系列图片，
• 基于3D结构和视角参数（即相机位置，朝向，固有标定和径向畸变）

过程

bundle adjustment可以根据所有点在图像中的投影作为标准，这个公式的意义就是最小化n个点在两幅图上投影的误差：

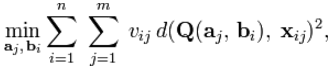
$n$个3D点在 $m$个view（拍摄场景）中;
向量 $X_{ij}$： $img_j$上的第 $i$个点projection（坐标）这个是实际点坐标 ;
值 $v_{ij}$：如果点 $i$在 $img_j$上有映射，则 $v_{ij}=1; else v_{ij}=0$; 可见，BundleAdjustment可以容忍特征点的丢失。
每个 $img_j$由向量 $a_j$参数化 ; 每个3D点由 $b_i$参数化
$Q(a_i,b_j)$:点 $i$在 $img_j$上的predicted projection 这个是理想点坐标
$d（x,y）$:向量 $x,y$的欧式距离

输出：

• 场景结构的3D点坐标
• 相对运动参数
• 相机的光学参数
• 最佳的三维结构和运动（如相机矩阵）参数估计。

目的

减少观测图像的点和参考图像（预测图像）的点之间位置投影变换（再投影）误差。

这最小化误差算法使用的是最小二乘算法，目前使用最为成功是Levenberg-Marquardt, 它具有易于实现，对大范围的初始估计能够快速收敛的优点。

data = load('sfmGlobe');

%%Refine the camera poses and points.

[xyzRefinedPoints,refinedPoses] = ...
    bundleAdjustment(data.xyzPoints,data.pointTracks,data.cameraPoses,data.intrinsics);



%% Display the refined camera poses and 3-D world points.
pcshow(xyzRefinedPoints,'VerticalAxis','y','VerticalAxisDir',...
    'down','MarkerSize',45);
hold on
%plotCamera(refinedPoses,'Size',0.1);
hold off
grid on

稀疏光束法平差SBA利用这种稀疏的特性

一个基于Levenberg-Marquardt(LM)算法的通用稀疏光束法平差SBA利用这种稀疏的特性，使用LM算法的简化的稀疏变量来降低计算的复杂度。

Sba是通用的，因为它保证了用户对于相机和三维结构的描述参数的定义的完全控制。

因此，它事实上可以支持任何多视重建问题的显示和参数化。

比如任意投影相机，部分的或完全标定的相机，由固定的三维点进行外方位元素（即姿态）的估计，精化本征参数，等等。

用户要想在这类问题中使用sba，只需要提供合适的程序对这些问题和参数来计算估计的图像投影和他们的函数行列式（Jacobian）。sba包含了检查用户提供的函数行列式的一致性的程序。

那些光束平差的工具，比如SBA、SSBA之类的虽然好，然而例子和教程都不够多且不够详细，让初学者难以上手。要传入的参数虽然有解释，然而却也不是十分清楚其含义，具体要怎么生成，生成为什么形式。

Matlab bundleAdjustment函数使用方法

函数说明

Matlab 在2016b版本后新加了bundleAdjustment函数，用于SLAM优化。不过该函数官网教程比较少，说的也较粗略。

使用方法
[xyzRefinedPoints,refinedPoses] = bundleAdjustment(xyzPoints,pointTracks,cameraPoses,intrinsics)

xyzPoints ：指的是三维点在世界坐标系中的坐标，采用N3的矩阵结构存储；
pointTracks ：指的图像点的坐标，注意此处要以（col, row）的方式表达，采用N2的矩阵结构存储；
cameraPoses ：指的世界坐标系在相机坐标系中的表示，此处包含的内容较多，需要采用table的数据结构存储，ViewId, Orientation, and Location一定要写对，不然会报错；
intrinsics ：相机的内参；

链接：https://blog.csdn.net/kangzhaobing123/article/details/103384110

附录 LM

% opti_LM_test2
% 测试了 数值分析 Timothy Sauer 中 4.4节中的 4.19例
clear all;clc;close all;
 
x1 = -1; y1 = 0;
x2 = 1; y2 = 1/2;
x3 = 1; y3 = -1/2;
 
R1 = 1; R2 = 1/2; R3 = 1/2;
%
syms x y;
r1 = sqrt( (x-x1)^2 + (y-y1)^2 )-R1;
r2 = sqrt( (x-x2)^2 + (y-y2)^2 )-R2;
r3 = sqrt( (x-x3)^2 + (y-y3)^2 )-R3;
 
r = ...
    [r1;
     r2;
     r3]
%
f = r
clear r1 r2 r3 R1 R2 R3 x1 x2 x3 y1 y2 y3 x y r;
%%
S = transpose(f)*f
f_var = symvar(f)
 
t_init = [0 0]    %  初始值，要给出
u = 2
v = 1.5
beta = 0.4
eps = 1.0e-6
tol = 1
%%
x = t_init
 
jacobian_f = jacobian(f,f_var)
%%
while tol>eps
    fxk = double(subs(f,f_var,x));
    Sxk = double(subs(S,f_var,x));  % step2: 计算 fxk Sxk
     
    delta_fxk = double(subs(jacobian_f,f_var,x));  % step3: 计算 delta_fxk
     
    delta_Sxk = transpose(delta_fxk)*fxk;   % step4: 计算 delta_Sxk
 
    while 1
        % step5: 计算Q，并解方程(Q+uI)delta_x = -delta_Sxk
        Q = transpose(delta_fxk)*delta_fxk;
        dx = -(Q+u*eye(size(Q)))\delta_Sxk;
         
        x1 = x + dx'; % 注意转置
         
        fxk = double(subs(f,f_var,x1));
        Sxk_new = double(subs(S,f_var,x1));
         
        tol = norm(dx);   % step6: 计算中止条件 norm(dx)<eps 是否满足，不满足转step 7
        if tol<=eps
            break;
        end
 
        % step7:
        if Sxk_new < Sxk+beta*transpose(delta_Sxk)*dx
            u = u/v;
            break;
        else
            u = u*v;
            continue;
        end
    end
     
    x = x1;
end
%%
format short;
opti_var_value = x1
minf = double(subs(S,f_var,opti_var_value))