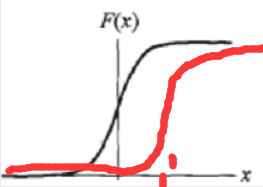
1.逻辑斯谛分布函数(logistic distribution): u为位置参数,y>0为形状参数---------->u控制下图对称中心点的X坐标值,y控制在中心附近增长速度的快慢。例如u=1,y=2的函数图像为红色曲线所示
F
(
X
)
=
P
(
X
<
=
x
)
=
1
1
+
e
−
(
x
−
u
)
/
y
F(X)=P(X<=x)=\frac{1}{1+e^{-(x-u)/y}}
F ( X ) = P ( X < = x ) = 1 + e − ( x − u ) / y 1
sigmoid函数满足逻辑斯谛分布,其位置参数u为0,形状参数y为1
2.逻辑斯谛概率密度函数:
f
(
x
)
=
F
,
(
x
)
=
e
−
(
x
−
u
)
/
y
y
(
1
+
e
−
(
x
−
u
)
/
y
)
2
f(x)=F^,(x)=\frac{e^{-(x-u)/y}}{y(1+e^{-(x-u)/y})^2}
f ( x ) = F , ( x ) = y ( 1 + e − ( x − u ) / y ) 2 e − ( x − u ) / y
二项逻辑斯谛回归模型(binomial logistic regression model)是一种分类模型,由条件概率分布P(Y|X)表示,这里举例都是随机变量Y=1或0
P
(
Y
=
1
∣
x
)
=
e
x
p
(
w
x
+
b
)
1
+
e
x
p
(
w
x
+
b
)
P(Y=1|x)=\frac{exp(wx+b)}{1+exp(wx+b)}
P ( Y = 1 ∣ x ) = 1 + e x p ( w x + b ) e x p ( w x + b )
P
(
Y
=
0
∣
x
)
=
1
1
+
e
x
p
(
w
x
+
b
)
P(Y=0|x)=\frac{1}{1+exp(wx+b)}
P ( Y = 0 ∣ x ) = 1 + e x p ( w x + b ) 1
p
1
−
p
\frac{p}{1-p}
1 − p p
l
o
g
i
t
(
p
)
=
l
o
g
p
1
−
p
logit(p)=log\frac{p}{1-p}
l o g i t ( p ) = l o g 1 − p p
l
o
g
i
t
(
P
(
Y
=
1
∣
x
)
1
−
P
(
Y
=
1
∣
x
)
)
=
l
o
g
(
e
x
p
(
w
x
+
b
)
)
=
w
x
+
b
logit(\frac{P(Y=1|x)}{1-P(Y=1|x)})=log(exp(wx+b))=wx+b
l o g i t ( 1 − P ( Y = 1 ∣ x ) P ( Y = 1 ∣ x ) ) = l o g ( e x p ( w x + b ) ) = w x + b 线性函数 ,输出Y的对数几率是有输入x的线性函数表示的模型,也就是再一次印证了逻辑斯谛回归模型是属于对数线性模型 .
对数线性模型:当一个概率函数P(Y|X)加上logit函数也就是logP(Y|X)=wx就称为该模型为对数线性模型。
换一个角度看,在输入x进行分类的线性函数w.x乃至于复杂的F(x)函数,其值域为实数,通过逻辑斯谛回归模型可以将w.x转换为概率,这时线性函数值接近正无穷,概率值就接近1,函数值接近负无穷,概率值就接近0,这样的模型就是逻辑斯谛回归模型(sigmod模型是特殊的逻辑斯谛回归模型)
P
(
Y
=
m
∣
x
)
=
e
x
p
(
w
x
+
b
)
1
+
e
x
p
(
w
x
+
b
)
P(Y=m|x)=\frac{exp(wx+b)}{1+exp(wx+b)}
P ( Y = m ∣ x ) = 1 + e x p ( w x + b ) e x p ( w x + b )
1.常见的参数估计方法:
本书中给出了通过极大似然估计(MLE)来进行参数估计
1.极大似然估计:在结果发生时,原因 为 概率最大的原因A。例如:一个程序员和一个哲学家 各写了一行字,当你看到Hello,World 时,那么你就会估计是程序员写的。
2.极大似然函数:
∏
i
=
1
N
P
(
x
i
;
θ
)
p
s
:
所
有
结
果
集
概
率
积
\prod_{i=1}^NP(x_i;\theta) ps:所有结果集概率积
∏ i = 1 N P ( x i ; θ ) p s : 所 有 结 果 集 概 率 积
对于给定的数据集T={(x1,y1),(x2,y2),(x3,y3),…(xn,yn)},其中xi属于R,yi属于0,1
P
(
Y
=
1
∣
x
)
=
π
(
x
)
,
P
(
Y
=
0
∣
x
)
=
1
−
π
(
x
)
P(Y=1|x)=\pi(x),P(Y=0|x)=1-\pi(x)
P ( Y = 1 ∣ x ) = π ( x ) , P ( Y = 0 ∣ x ) = 1 − π ( x )
∏
i
=
1
N
[
π
(
x
i
)
]
y
i
[
1
−
π
(
x
)
]
1
−
y
i
\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x)]^{1-y_i}
i = 1 ∏ N [ π ( x i ) ] y i [ 1 − π ( x ) ] 1 − y i
L
(
w
)
=
l
o
g
∏
i
=
1
N
[
π
(
x
i
)
]
y
i
[
1
−
π
(
x
)
]
1
−
y
i
=
∑
i
=
1
N
y
i
l
o
g
π
i
+
(
1
−
y
i
)
l
o
g
(
1
−
π
i
)
=
∑
i
=
1
N
y
i
l
o
g
π
i
1
−
π
i
+
l
o
g
(
1
−
π
i
)
=
∑
i
=
1
N
y
i
(
w
.
x
i
)
−
l
o
g
(
1
+
e
x
p
(
x
.
x
i
)
)
L(w)=log\prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x)]^{1-y_i}=\sum_{i=1}^Ny_ilog\pi_i+(1-y_i)log(1-\pi_i)=\sum_{i=1}^Ny_ilog\frac{\pi_i}{1-\pi_i}+log(1-\pi_i)=\sum_{i=1}^Ny_i(w.x_i)-log(1+exp(x.x_i))
L ( w ) = l o g i = 1 ∏ N [ π ( x i ) ] y i [ 1 − π ( x ) ] 1 − y i = i = 1 ∑ N y i l o g π i + ( 1 − y i ) l o g ( 1 − π i ) = i = 1 ∑ N y i l o g 1 − π i π i + l o g ( 1 − π i ) = i = 1 ∑ N y i ( w . x i ) − l o g ( 1 + e x p ( x . x i ) )
w
‾
\overline w
w
P
(
Y
=
1
∣
x
)
=
e
x
p
(
w
‾
x
+
b
)
1
+
e
x
p
(
w
‾
x
+
b
)
P(Y=1|x)=\frac{exp(\overline wx+b)}{1+exp(\overline wx+b)}
P ( Y = 1 ∣ x ) = 1 + e x p ( w x + b ) e x p ( w x + b )
P
(
Y
=
0
∣
x
)
=
1
1
+
e
x
p
(
w
‾
x
+
b
)
P(Y=0|x)=\frac{1}{1+exp(\overline wx+b)}
P ( Y = 0 ∣ x ) = 1 + e x p ( w x + b ) 1
1.假设离散型随机变量Y的取值集合是{1,2,… ,K},那么多项逻辑斯谛回归模型是
P
(
Y
=
k
∣
x
)
=
e
x
p
(
w
k
.
x
)
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
P(Y=k | x)=\frac{exp(w_k.x)}{\sum_{k=1}^{K}exp(w_k.x)}
P ( Y = k ∣ x ) = ∑ k = 1 K e x p ( w k . x ) e x p ( w k . x )
P
(
Y
=
K
∣
x
)
=
e
x
p
(
w
K
.
x
)
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
P(Y=K | x)=\frac{exp(w_K.x)}{\sum_{k=1}^{K}exp(w_k.x)}
P ( Y = K ∣ x ) = ∑ k = 1 K e x p ( w k . x ) e x p ( w K . x ) 2.多项参数模型估计类推为----->
P
(
Y
=
1
∣
x
)
=
e
x
p
(
w
1
.
x
)
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
,
.
.
.
,
P
(
Y
=
K
∣
x
)
=
e
x
p
(
w
K
.
x
)
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
P(Y=1|x)=\frac{exp(w_1.x)}{\sum_{k=1}^{K}exp(w_k.x)},... ,P(Y=K|x)=\frac{exp(w_K.x)}{\sum_{k=1}^{K}exp(w_k.x)}
P ( Y = 1 ∣ x ) = ∑ k = 1 K e x p ( w k . x ) e x p ( w 1 . x ) , . . . , P ( Y = K ∣ x ) = ∑ k = 1 K e x p ( w k . x ) e x p ( w K . x ) 3.多项极大似然估计函数为,
I
(
y
i
=
k
)
I(y_i=k)
I ( y i = k )
∏
k
=
1
K
∏
i
=
1
N
e
x
p
(
w
k
.
x
)
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
I
(
y
i
=
k
)
\prod_{k=1}^K\prod_{i=1}^N\frac{exp(w_k.x)}{\sum_{k=1}^{K}exp(w_k.x)}^{I(y_i=k)}
k = 1 ∏ K i = 1 ∏ N ∑ k = 1 K e x p ( w k . x ) e x p ( w k . x ) I ( y i = k ) 4.对数似然函数为------->
L
(
w
)
=
l
o
g
∏
k
=
1
K
∏
i
=
1
N
e
x
p
(
w
k
.
x
)
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
I
(
y
i
=
k
)
=
∑
k
=
1
K
∑
i
=
1
N
I
(
y
i
=
k
)
×
[
(
w
k
.
x
)
−
l
o
g
∑
k
=
1
K
e
x
p
(
w
k
.
x
)
]
L(w)=log\prod_{k=1}^K\prod_{i=1}^N\frac{exp(w_k.x)}{\sum_{k=1}^{K}exp(w_k.x)}^{I(y_i=k)}=\sum_{k=1}^K\sum_{i=1}^N{I(y_i=k)}\times [(w_k.x)-log\sum_{k=1}^{K}exp(w_k.x)]
L ( w ) = l o g k = 1 ∏ K i = 1 ∏ N ∑ k = 1 K e x p ( w k . x ) e x p ( w k . x ) I ( y i = k ) = k = 1 ∑ K i = 1 ∑ N I ( y i = k ) × [ ( w k . x ) − l o g k = 1 ∑ K e x p ( w k . x ) ] 接下来求L(w)的最大值,得到最优参数
w
1
w_1
w 1
w
2
w_2
w 2
w
K
w_K
w K
5.总结:多项逻辑斯谛回归参数
w
i
w_i
w i
1.最大熵原理:在所有学习概率模型中,熵最大的模型是最好的模型:
H
(
p
)
=
−
∑
i
=
1
n
p
(
x
)
l
o
g
p
(
x
)
H(p)=-\sum_{i=1}^np(x)log p(x)
H ( p ) = − i = 1 ∑ n p ( x ) l o g p ( x )
eg:世界末日的时候,当我知道你为人类做出巨大贡献时,可以提高你转移的概率,当身份没有区别的时候等可能性是最好的方案(最容易令人信服),最大熵模型就是这个思路
2.书中给出一个栗子:假设随机变量X有5个取值{A,B,C,D,E},要估计取各个值的概率P(A),P(B),P( C ),P(D),P(E) 满足这个约束条件的概率分布有很多,如果没有其他信息的约束,则认为分布中各个值概率是相等的 当能从其他知识中获得一些约束条件,继续按照约束条件进行估计,这样的概率模型学习方法正式遵循了最大熵原理。
给定一个数据集T={(x1,y1),(x2,y2),(x3,y3),…(xn,yn)},首先给出了联合分布P(x,y)的经验分布和边缘分布P(x)的经验分布
P
‾
(
X
=
x
,
Y
=
y
)
=
v
(
X
=
x
,
Y
=
y
)
N
\overline P(X=x,Y=y)=\frac{v(X=x,Y=y)}{N}
P ( X = x , Y = y ) = N v ( X = x , Y = y )
P
‾
(
X
=
x
)
=
v
(
X
=
x
)
N
\overline P(X=x)=\frac{v(X=x)}{N}
P ( X = x ) = N v ( X = x )
f
(
x
,
y
)
=
1
,
x
与
y
满
足
某
一
事
实
0
,
否
则
f(x,y)=\frac{1,x与y满足某一事实}{0,否则}
f ( x , y ) = 0 , 否 则 1 , x 与 y 满 足 某 一 事 实
E
P
‾
(
f
)
=
∑
x
,
y
P
‾
(
x
,
y
)
f
(
x
,
y
)
E_{\overline P}(f)=\sum_{x,y}\overline P(x,y)f(x,y)
E P ( f ) = x , y ∑ P ( x , y ) f ( x , y )
E
P
(
f
)
=
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
f
(
x
,
y
)
,
因
为
P
‾
(
x
)
P
(
y
∣
x
)
=
P
(
x
,
y
)
E_{ P}(f)=\sum_{x,y}\overline P(x)P(y|x)f(x,y),因为\overline P(x)P(y|x)=P(x,y)
E P ( f ) = x , y ∑ P ( x ) P ( y ∣ x ) f ( x , y ) , 因 为 P ( x ) P ( y ∣ x ) = P ( x , y )
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
f
(
x
,
y
)
=
=
∑
x
,
y
P
‾
(
x
,
y
)
f
(
x
,
y
)
\sum_{x,y}\overline P(x)P(y|x)f(x,y)==\sum_{x,y}\overline P(x,y)f(x,y)
x , y ∑ P ( x ) P ( y ∣ x ) f ( x , y ) = = x , y ∑ P ( x , y ) f ( x , y ) (学习的目的就是求出在给出的X条件下Y的概率 )为:
H
(
P
)
=
−
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
l
o
g
P
(
y
∣
x
)
H(P)=-\sum_{x,y}\overline P(x)P(y|x)logP(y|x)
H ( P ) = − x , y ∑ P ( x ) P ( y ∣ x ) l o g P ( y ∣ x )
m
a
x
H
(
P
)
=
−
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
l
o
g
P
(
y
∣
x
)
s
.
t
.
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
f
(
x
,
y
)
=
=
∑
x
,
y
P
‾
(
x
,
y
)
f
(
x
,
y
)
∑
y
P
(
y
∣
x
)
=
1
max H(P)=-\sum_{x,y}\overline P(x)P(y|x)logP(y|x) \\ s.t.\sum_{x,y}\overline P(x)P(y|x)f(x,y)==\sum_{x,y}\overline P(x,y)f(x,y)\\\sum_yP(y|x)=1
m a x H ( P ) = − x , y ∑ P ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) s . t . x , y ∑ P ( x ) P ( y ∣ x ) f ( x , y ) = = x , y ∑ P ( x , y ) f ( x , y ) y ∑ P ( y ∣ x ) = 1 1.按照习惯转换为最小化问题
m
i
n
H
(
P
)
=
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
l
o
g
P
(
y
∣
x
)
s
.
t
.
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
f
(
x
,
y
)
=
=
∑
x
,
y
P
‾
(
x
,
y
)
f
(
x
,
y
)
∑
y
P
(
y
∣
x
)
=
1
min H(P)=\sum_{x,y}\overline P(x)P(y|x)logP(y|x) \\ s.t.\sum_{x,y}\overline P(x)P(y|x)f(x,y)==\sum_{x,y}\overline P(x,y)f(x,y)\\\sum_yP(y|x)=1
m i n H ( P ) = x , y ∑ P ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) s . t . x , y ∑ P ( x ) P ( y ∣ x ) f ( x , y ) = = x , y ∑ P ( x , y ) f ( x , y ) y ∑ P ( y ∣ x ) = 1 2.将约束最优化问题转为无约束最优化的对偶问题,首先引进拉格朗日乘子
w
0
w_0
w 0
w
1
w_1
w 1
w
n
w_n
w n
L
(
P
,
W
)
=
−
H
(
P
)
+
w
0
[
1
−
∑
P
(
y
∣
x
)
]
+
∑
i
=
1
n
w
i
(
E
P
‾
(
f
i
)
−
E
p
(
f
i
)
)
=
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
l
o
g
P
(
y
∣
x
)
+
w
0
[
1
−
∑
P
(
y
∣
x
)
]
+
∑
i
=
1
n
[
∑
x
,
y
P
‾
(
x
)
P
(
y
∣
x
)
f
(
x
,
y
)
−
∑
x
,
y
P
‾
(
x
,
y
)
f
(
x
,
y
)
]
L(P,W)=-H(P)+w_0[1-\sum P(y|x)]+\sum_{i=1}^n w_i(E_{\overline P}(f_i)-E_p(f_i))=\sum_{x,y}\overline P(x)P(y|x)logP(y|x) +w_0[1-\sum P(y|x)]+\sum_{i=1}^n [\sum_{x,y}\overline P(x)P(y|x)f(x,y)-\sum_{x,y}\overline P(x,y)f(x,y)]
L ( P , W ) = − H ( P ) + w 0 [ 1 − ∑ P ( y ∣ x ) ] + i = 1 ∑ n w i ( E P ( f i ) − E p ( f i ) ) = x , y ∑ P ( x ) P ( y ∣ x ) l o g P ( y ∣ x ) + w 0 [ 1 − ∑ P ( y ∣ x ) ] + i = 1 ∑ n [ x , y ∑ P ( x ) P ( y ∣ x ) f ( x , y ) − x , y ∑ P ( x , y ) f ( x , y ) ] 3.最优化原始问题为
m
i
n
P
∣
m
a
x
w
L
(
P
,
W
)
min_P |max_wL(P,W)
m i n P ∣ m a x w L ( P , W )
m
a
x
w
∣
m
i
n
P
L
(
P
,
W
)
max_w |min_P L(P,W)
m a x w ∣ m i n P L ( P , W ) 拉格朗日对偶问题—解决最优化约束问题