オリジナルリンクします。https://blog.csdn.net/abel_liujinquan/article/details/89435686z
作者ます。https://blog.csdn.net/Abel_Liujinquan
1、バイナリツリーの概念
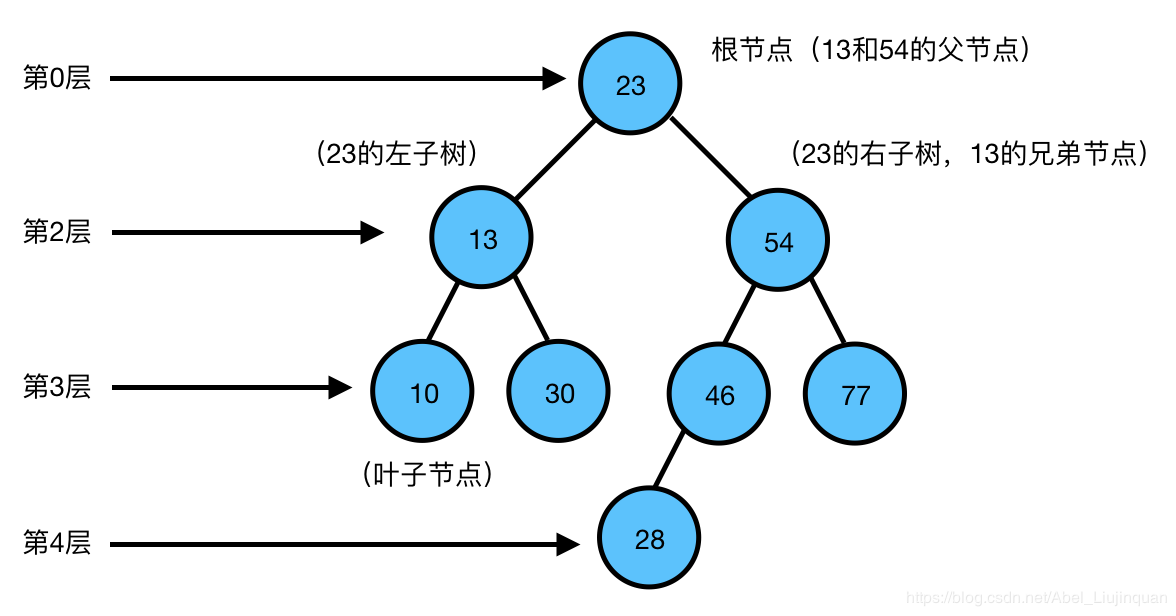
二分木:各ノードは最大2つの分岐ツリー構造(2未満の分岐度)を有し、ツリーは空であってもよいです。
ルート:ツリーの最上位ノードはルートノードと呼ばれています。
左と右のサブツリー:左のブランチ内のノードは、左の部分木と呼ばれ、右のブランチは、右部分木と呼ばれています。
子供について:ルートノードの左と右の枝内のノードは、左と右の子と呼ばれます。
兄弟ノード:互いに兄弟の同じ親ノードとノード。
次数ノード:ノードはサブツリーの数を有しています。
リーフノード:子を持たないノードは葉ノードと呼ばれています。
内部ノード:非リーフノードが内部ノードと呼ばれます。
ルートレベル:ルートノードから始まる定義された、第一層の根、第二層はノードまで、子のルートであるため、カウント。
ツリーの深さ、高さ:深さまたは高さの二分木と呼ばれる二分木におけるノードの最大レベル。
2、バイナリ分類
1)、完全なバイナリツリー
バイナリツリーで、最後の1を除いて、それがいっぱいになって、完全または最後の層である、または複数のノードの連続権利の欠如は、完全2分木になります。図示のように:

2)完全二分木
Kの深さ、及びある2K + 1-1 2 ^ {K + 1} -12
バイナリK + 1-1ノードは完全なバイナリツリーになります。図示のように:
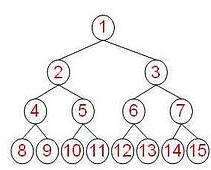
3)、二分探索木(バイナリ検索ツリー)
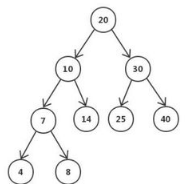
また、バイナリ検索ツリー、バイナリツリー分類として知られ、左の部分木は空のツリーノードである、またはすべて満たすことができるノード<ノードと<ノードの右サブツリーは、ノードが示すように、存在しない値に等しいです。

4)、平衡二分木(平衡二分木)
構造的にバランスのバイナリ検索ツリーは、図に示されるように、すなわち、リーフノードは、操作を見つけて削除するには、1の深さは、完成O(LOGN)に挿入することができる超えていない構造の一般的なバランスバイナリツリーはAVL、赤色を有します黒の木。
5)、AVL木
高バランスツリーは、自己均衡バイナリ検索ツリー第一の発明、任意のノード1の二人の息子サブツリー間の最大高低差であり、知られており、付加および欠失は、ツリーのバランスを再調整するために回転以上する必要があるかもしれませんツリー、図に示されている木。
元平衡(非AVL木):

平衡化後(AVL木):

6)、赤黒木(赤黒木)
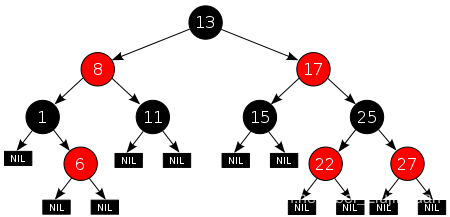
是一种自平衡二叉查找树,又称为“对称二叉B树”,除了满足所有二叉查找树的要求之外还需要满足以下要求:
(1)节点是红色或者是黑色的
(2)跟节点是黑色的
(3)每个叶子节点都是黑色的(叶子是NIL节点)
(4)每个红色节点必须有两个黑色节点(从叶子到根节点的所有简单路径上不可能有两个连续的红色节点)
(5)从任一节点到其每个叶子的所有简单路径都饱和相同数目的节点
注:
NIL节点就是空节点,二叉树中庸NIL节点代替NULL
简单路径:指顶点序列中顶点不重复出现的路径
3、二叉树的性质
性质1:在非空二叉树的第i层上最多有2^i−1 个节点。
性质2:深度为K的二叉树最多有2^k-1个节点。
性质3:对于任意一棵二叉树,如果度为0的节点个数为n0,度为2的节点个数为n2,则n0 = n2 + 1。
性质4:具有n个节点的完全二叉树的深度k=⌊log2n⌋+1。
性质5:对于含n个节点的完全二叉树中编号为i(1≤ \leq≤i≤ \leq≤n)的节点:
- 如果i=1,则i节点是这可完全二叉树的根,没有双亲,否则其双亲的编号为⌊i/2⌋。
- 如果2i>n,则i节点没有左孩子,否则其左孩子的编号为2i。
- 如果2i+1>n,则i节点没有右孩子,否则其有孩子的编号为2i+1。