1.決め手
1.1アルゴリズムの選択ポリシー
問題の1.2サイズ
1.3プログラミング言語
コンパイラ1.4によって生成されたマシンコードの品質
スピード1.5のコンピュータ実行可能な命令
2.その他の影響要素
3.問題のスケール(時間複雑さ)
3.1定義
「ワークロードを実行して、」特定のアルゴリズムのサイズは、(通常、整数nとして表される)唯一の問題の規模に依存し、またはそれは、問題の大きさの関数であること。
問題のサイズnが大きくなるにつれて、成長及びFの同一のアルゴリズム実行時間(n)は成長率が、場合として記録することができる:T(N)= O( F(N))、 (N)Tとしても知られていますアルゴリズムの(漸近)時間の複雑さのために。
アルゴリズムは、制御構造(シーケンシャル、分岐およびループ3種類)であり、そして本来の動作(操作の固有のデータタイプを参照)の設定、時間を実行すると、両方の複合効果に依存します。
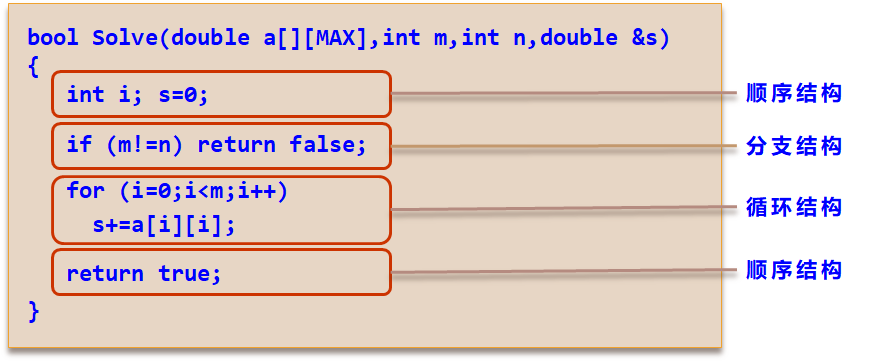
3.2時間推定アルゴリズムの複雑さ
(時間計算)
3.2.1定義
主要な問題を操作を選択するためのアルゴリズムの基本的な動作から検討され、回数は、アルゴリズムにおける基本的な動作は、繰り返し時間基準を実行しているの尺度として実行されます。
「基本的な操作は、」操作が実行時間やアルゴリズムに比例した回数を繰り返していることを意味します。
=Σアルゴリズム本来の動作(I)の実行時間は、元の動作(I)実行時間の実行回数を×
詳細なアルゴリズムの実行時間と回数が実行され、元に比例します
= +オリジナルアルゴリズム演算制御構造(操作の固有のデータ型)
1 2つの行列乗算 EG1 2つの行列の乗算 ボイドのMult(INTA []、int型 B []、INT&{C []) // 2次元メモリマトリクスアレイ素子を、Cであり、そしてBの生成物 のための(I = 1 ; I <= N; ++ I){ ため(Jは= 1。 ; J <= N-; ++ J){ C [I、J] = 0 ; のための(K = 。1 ; K <= N; ++ K) C [I、J] + = A [I、K] * B [K、J]; } } }基本的な操作:乗算時間複雑:O(N ^ 3。)
2 [ソート

3バブルソート

4次再帰関数ファクト(n)は、時間複雑度分析有する int型 FACT(INT N-){ IF - (<= N 1)リターン(1)、(1 ) 他の リターン(N * FACT(N- 1))を;(2 ) } 溶液:う事実(n)の時間T(n)を実行する複雑な関数であり、 関数ステートメント(1実行時間)がO(1 )、 ステートメント(2)実行時間: T(N- 1)+ O(1 ) 前記O(1 )基本的な動作時間として、 このように:T(N) = O(1)+ T(N- 1。) = O(1)入出力+(1)+ T(N- 2 ) = ... =(N- 1)* O(1)T +(1 ) = O、N- *(1 ) = Oは、(N-)であります事実(n)の時間計算量はO(n)です。
アルゴリズムの時間計算の一般的なステップの3.2.2分析

3.2.3プログレッシブシンボル
N問題アルゴリズムのサイズ、通常、大きなn個のOと成長し、アルゴリズムの実行時間との関係を示し、大Ω及びΘ三個のプログレッシブシンボルとします。
3.2.3.1ランダウの記号
定義
定義1(ランダウの記号)、F(N)= O(G(N))(として読み取る "F(n)はgである(n)が大きいOである")場合にのみ、通常の量のCの存在およびN0場合、そのよう場合n≥n0時間は、(N)≤cg(N)F、すなわち、G(n)はF(n)が上限です。
3N + 2 = O(n)は 、 ≧2、3N +2≤4nため。
10n2 + 4N + 2 = O( N4)、 時間ので≧2、10n2 + 4N +2≤10n4。
上限の速度を記述するために使用ランダウの記号は、入力サイズがNである場合、G(n)の成長として、それはアルゴリズムを消費する最大時間は、と言うことであるせいぜい速くF(n)は成長を表します。下位に結合し、より価値のある結果、従って、10Nへ2 + 4N + 2、O(N 2 Oより)(N- 4)の値。
常に最も貴重なG(n)を用いて、大きな時間表記Oとアルゴリズムは、呼び出さ表す場合、「上限コンパクト」または「上部本当にタイト結合。」
一般的には、場合![]() があり
があり![]()
時間の複雑さのいくつかの種類との関係
説明:
ちょうどその成長を見つけるために、正確基本動作実行時間(または周波数文)を算出することが困難である場合、またはn個のオーダーの1 最悪、最良である具体2とすることができるアルゴリズムの時間複雑(また、最悪としても知られる)、平均3つのケースが論じ。
特に明記しない限り、時間に通常の最悪の場合の複雑さを参照してください。
![]()
例
1 2つの行列乗算
EG1 2つの行列の乗算
ボイドのMult(INTA []、B []、INTおよびInt C []){
// 2次元メモリマトリクスアレイ素子、cは、aとbであります生成物
のための(I = 1; I <= N; ++ I){
ため(Jは= 1; J <= N-; ++ J){ C [I、J] = 0 ; (K = 1 ; K <= N; ++ K)C [I、J] + = A [I、K] * B [K、J];}}}基本的な操作:乗算時間複雑:O(N ^ 3)
2 [ソート

3バブルソート

4有如下递归函数fact(n),分析其时间复杂度
int fact(int n){
if(n<=1) return(1); (1)
else return(n*fact(n-1)); (2)
}
解:设fact(n)的运行时间复杂函数是T(n),
该函数中语句(1)的运行时间是O(1),
语句(2)的运行时间为:T(n-1)+O(1), 其中O(1)为基本运算时间, 因此: T(n) = O(1)+T(n-1) = O(1)+O(1)+T(n-2) = …… = (n-1)*O(1)+T(1) = n*O(1) = O(n)则fact(n)的时间复杂度为O(n)。
3.2.3.2 大Ω符号
定义2(大Ω符号),f(n)= Ω(g(n))(读作“f(n)是g(n)的大Ω”)当且仅当存在正常量c和nθ,使当n≥n0时,f(n)≥cg(n),即g(n)为f(n)的下界。
如3n+2=Ω(n),因为当n≥1时,3n+2≥3n。
10n2+4n+2=Ω(n2),因为当n≥1时,10n2+4n+2≥n2。
大Ω符号用来描述增长率的下界,表示f(n)的增长最少像g(n) 增长的那样快,也就是说,当输入规模为n时,算法消耗时间的最小值。
与大O符号对称,这个下界的阶越高,结果就越有价值,所以,对于10n2+4n+2,Ω(n2)比Ω(n) 有价值。一个算法的时间用大Ω符号表示时,总是采用最有价值的g(n)表示,称之为“紧凑下界”或“紧确下界”。
一般地,如果![]() ,有
,有![]() 。
。
3.2.3.3大Θ符号
定义3(大Θ符号),f(n)= Θ(g(n))(读作“f(n)是g(n)的大Θ”)当且仅当存在正常量c1、c2和n0,使当n≥n0时,有c1g(n)≤f(n)≤c2g(n),即g(n)与f(n)的同阶。
如3n+2=Θ (n),10n2+4n+2=Θ(n2)。
一般地,如果![]() ,有f(n)=Θ(nm)。
,有f(n)=Θ(nm)。
大Θ符号比大O符号和大Ω符号都精确,f(n)=Θ(g(n),当且仅当g(n)既是f(n)的上界又是f(n)的下界。
3.2.3.4关系
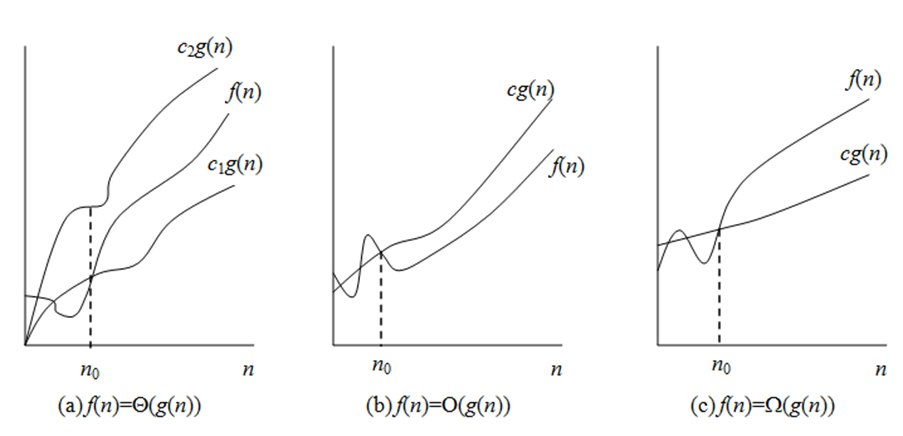
3.3算法的最好、最坏和平均情况
设一个算法的输入规模为n,Dn是所有输入的集合,任一输入I∈Dn,P(I)是I出现的概率,有ΣP(I) =1,T(I)是算法在输入I下所执行的基本语句次数,则该算法的平均执行时间为:A(n)=![]() 。
。
也就是说算法的平均情况是指用各种特定输入下的基本语句执行次数的带权平均值。
算法的最好情况为:G(n)=![]() ,是指算法在所有输入I下所执行基本语句的最少次数。
,是指算法在所有输入I下所执行基本语句的最少次数。
算法的最坏情况为:W(n)=![]() ,是指算法在所有输入I下所执行基本语句的最大次数。
,是指算法在所有输入I下所执行基本语句的最大次数。
4.算法选用的策略
4.3非递归算法的时间复杂度分析
对于非递归算法,分析其时间复杂度相对比较简单,关键是求出代表算法执行时间的表达式。
通常是算法中基本语句的执行次数,是一个关于问题规模n的表达式,然后用渐进符号来表示这个表达式即得到算法的时间复杂度。
4.2递归算法的时间复杂度分析
递归算法是采用一种分而治之的方法,把一个“大问题”分解为若干个相似的“小问题”来求解。
对递归算法时间复杂度的分析,关键是根据递归过程建立递推关系式,然后求解这个递推关系式,得到一个表示算法执行时间的表达式,最后用渐进符号来表示这个表达式即得到算法的时间复杂度。