Enlace original: https://ai.plainenglish.io/graph-convolutional-networks-gcn-baf337d5cb6b

En esta publicación, vamos a echar un vistazo de cerca a una de las conocidas redes neuronales de Graph llamada GCN. Primero, obtendremos la intuición para ver cómo funciona, luego profundizaremos en las matemáticas detrás de esto.

¿Por qué gráficos?

Ejemplos de gráficos. (Imagen de [1])

Tareas en gráficos

Clasificación de nodos: predecir un tipo de un nodo dado
Predicción de enlaces: predecir si dos nodos están enlazados
Detección de comunidades: identifique grupos de nodos densamente vinculados
Similitud de red: qué tan similares son dos (sub)redes

Ciclo de vida del aprendizaje automático

En el gráfico, tenemos las características de los nodos (los datos de los nodos) y la estructura del gráfico (cómo se conectan los nodos).

Para el primero, podemos obtener fácilmente los datos de cada nodo. Pero cuando se trata de la estructura, no es trivial extraer información útil de ella. Por ejemplo, si 2 nodos están cerca uno del otro, ¿debemos tratarlos de manera diferente a otros pares? ¿Qué hay de los nodos de alto y bajo grado? De hecho, cada tarea específica puede consumir mucho tiempo y esfuerzo solo para la ingeniería de funciones, es decir, para destilar la estructura en nuestras funciones.

Ingeniería de características en grafos. (Imagen de [1])

Sería mucho mejor obtener de alguna manera tanto las características del nodo como la estructura como entrada, y dejar que la máquina descubra qué información es útil por sí misma.

Es por eso que necesitamos el Aprendizaje de Representación Gráfica.

Queremos que el gráfico pueda aprender la "ingeniería de características" por sí mismo. (Imagen de [1])

Redes convolucionales gráficas (GCN)

Artículo: Clasificación semisupervisada con redes convolucionales gráficas (2017) [3]

GCN es un tipo de red neuronal convolucional que puede trabajar directamente en gráficos y aprovechar su información estructural.

resuelve el problema de clasificar nodos (como documentos) en un gráfico (como una red de citas), donde las etiquetas solo están disponibles para un pequeño subconjunto de nodos (aprendizaje semisupervisado).

Ejemplo de aprendizaje semisupervisado en gráficos. Algunos nodos no tienen etiquetas (nodos desconocidos).

Ideas principales

Como sugiere el nombre "Convolucional", la idea fue de Imágenes y luego llevada a Gráficos. Sin embargo, cuando las Imágenes tienen una estructura fija, los Gráficos son mucho más complejos.

Idea de convolución de imágenes a gráficos. (Imagen de [1])

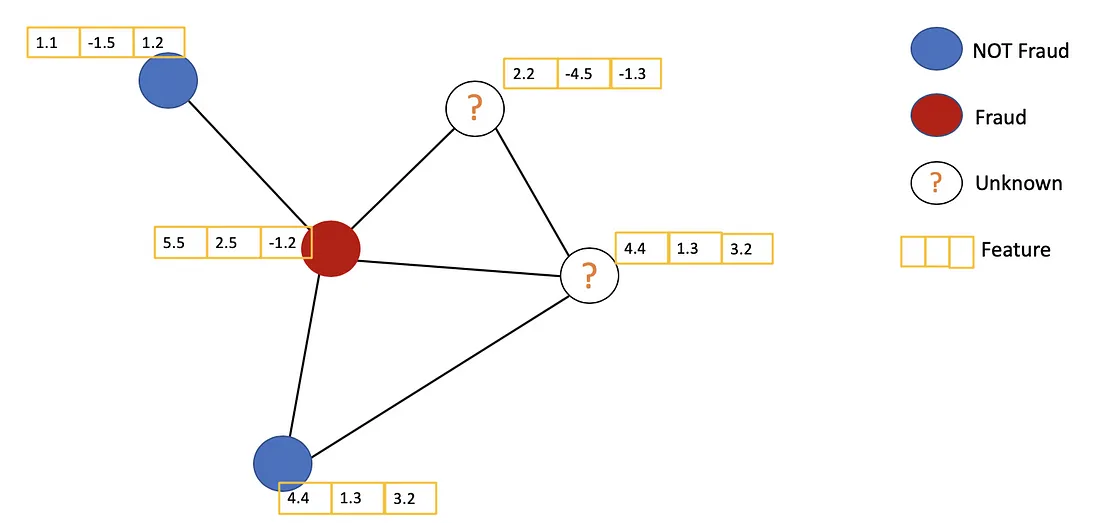
La idea general de GCN : para cada nodo, obtenemos la información de características de todos sus vecinos y, por supuesto, la característica de sí mismo. Supongamos que usamos la función promedio(). Haremos lo mismo para todos los nodos. Finalmente, alimentamos estos valores promedio en una red neuronal.

En la siguiente figura, tenemos un ejemplo simple con una red de citas. Cada nodo representa un trabajo de investigación, mientras que los bordes son las citas. Aquí tenemos un paso previo al proceso. En lugar de utilizar los documentos sin procesar como funciones, convertimos los documentos en vectores (utilizando la incrustación de PNL, por ejemplo, tf–idf, Doc2Vec).

Consideremos el nodo naranja. En primer lugar, obtenemos todos los valores de las características de sus vecinos, incluido él mismo, y luego tomamos el promedio. El resultado se pasará a través de una red neuronal para devolver un vector resultante.

La idea principal de GCN. Considere el nodo naranja en el medio. Primero, tomamos el promedio de todos sus vecinos, incluido él mismo. Después de eso, el valor promedio se pasa a través de una red neuronal. Tenga en cuenta que, en GCN, simplemente usamos una capa completamente conectada. En este ejemplo, obtenemos vectores de 2 dimensiones como salida (2 nodos en la capa completamente conectada).

En la práctica, podemos usar funciones agregadas más sofisticadas en lugar de la función promedio. También podemos apilar más capas una encima de la otra para obtener una GCN más profunda. La salida de una capa se tratará como la entrada de la siguiente capa.

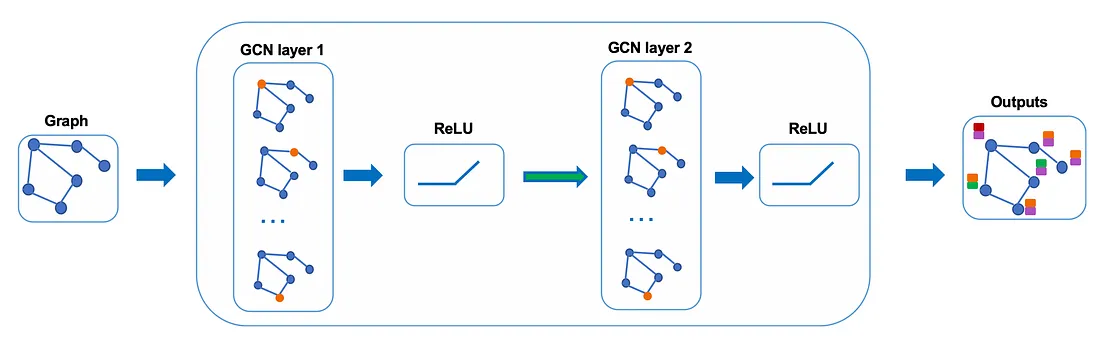
Ejemplo de GCN de 2 capas: la salida de la primera capa es la entrada de la segunda capa.
Echemos un vistazo más de cerca a las matemáticas para ver cómo funciona realmente.

La intuición y las matemáticas detrás

Primero, necesitamos algunas notaciones:

Dado un grafo no dirigido $GRAMO = (V, E)$ con $N$ nodos $v_i \in V$ , aristas $(v_i, v_j) \in E$ , una matriz de adyacencia $\in R^{N×N}$ (binario o ponderado), matriz de grados $D_{ii} = \sum_j Α_{ij}$ y matriz de vectores de características $\in R^{N×C}$ (N son #nodos, C son las #dimensiones de un vector de características).

Consideremos un gráfico G como se muestra a continuación.

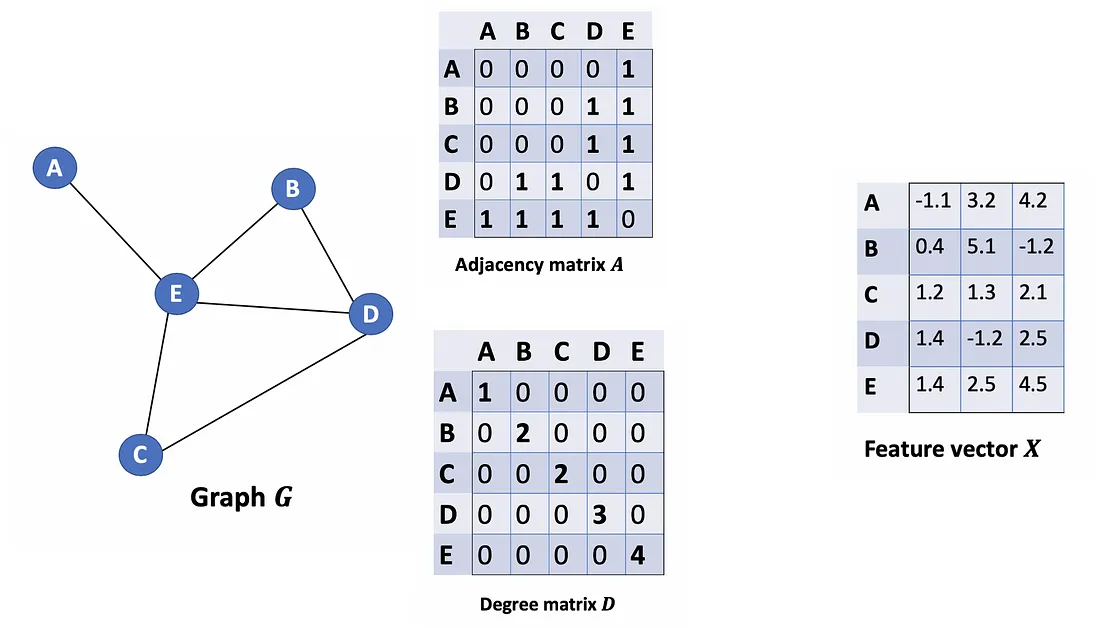
Del gráfico G, tenemos una matriz de adyacencia A y una matriz de Grado D. También tenemos una matriz de características X.

¿Cómo podemos obtener todos los valores de características de los vecinos para cada nodo? La solución está en la multiplicación de A y X.

Eche un vistazo a la primera fila de la matriz de adyacencia, vemos que el nodo A tiene una conexión con E. La primera fila de la matriz resultante es el vector de características de E, al que se conecta A (Figura siguiente). De manera similar, la segunda fila de la matriz resultante es la suma de los vectores de características de D y E. Al hacer esto, podemos obtener la suma de los vectores de todos los vecinos.

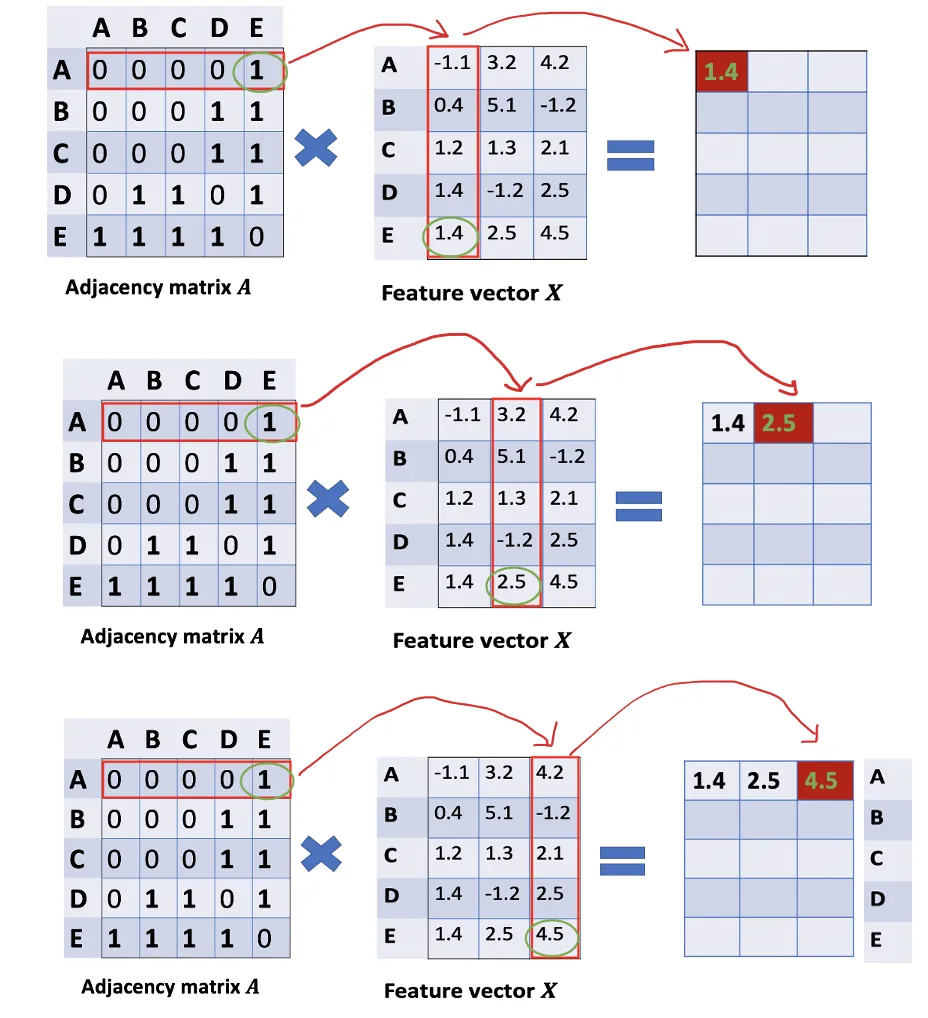
Calcule la primera fila de la "matriz vectorial de suma" AX

Todavía hay algunas cosas que necesitan mejorar aquí.

Echamos de menos la característica del nodo en sí. Por ejemplo, la primera fila de la matriz de resultados también debe contener características del nodo A.
En lugar de la función sum(), necesitamos tomar el promedio, o incluso mejor, el promedio ponderado de los vectores de características de los vecinos. ¿Por qué no usamos la función sum()? La razón es que cuando se usa la función sum(), es probable que los nodos de grado alto tengan vectores v enormes, mientras que los nodos de grado bajo tienden a tener vectores agregados pequeños, lo que más tarde puede provocar la explosión o la desaparición de gradientes (p. ej., cuando se usa sigmoide ). Además, las redes neuronales parecen ser sensibles a la escala de los datos de entrada. Por lo tanto, necesitamos normalizar estos vectores para deshacernos de los posibles problemas.

En el problema (1), podemos solucionarlo agregando una matriz de identidad I a A para obtener una nueva matriz de adyacencia Ã.

$\tilde{A}=A+\lambda I_N$

Elija lambda = 1 (la característica del nodo en sí es tan importante como sus vecinos), tenemos Ã = A + I. Tenga en cuenta que podemos tratar a lambda como un parámetro entrenable, pero por ahora, solo asigne la lambda a 1, y incluso en el documento, lambda simplemente se asigna a 1.

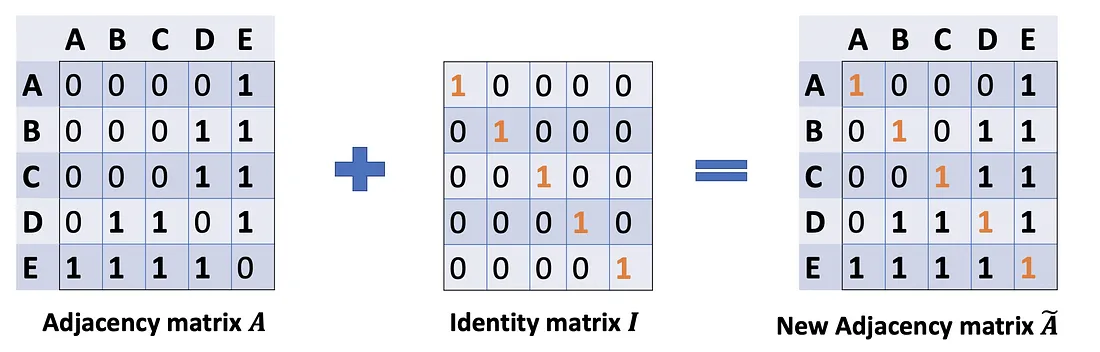
Al agregar un autobucle a cada nodo, tenemos la nueva matriz de adyacencia.

Problema (2): Para el escalado de matrices, generalmente multiplicamos la matriz por una matriz diagonal. En este caso, queremos tomar el promedio de la función de suma, o matemáticamente, escalar la matriz vectorial de suma ÃX de acuerdo con los grados del nodo. El presentimiento nos dice que nuestra matriz diagonal utilizada para escalar aquí es algo relacionado con la matriz de Grado D̃ (¿Por qué D̃, no D? Porque estamos considerando la matriz de Grado D̃ de la nueva matriz de adyacencia Ã, ya no A).

El problema ahora es cómo queremos escalar/normalizar los vectores de suma. En otras palabras:

¿Cómo pasamos la información de los vecinos a un nodo específico?

Comenzaríamos con nuestro viejo amigo promedio. En este caso, entra en juego D̃ inversa (es decir, D̃^{-1}). Básicamente, cada elemento en D̃ inversa es el recíproco de su término correspondiente de la matriz diagonal D̃.

Por ejemplo, el nodo A tiene un grado de 2, entonces multiplicamos los vectores de suma del nodo A por 1/2, mientras que el nodo E tiene un grado de 5, debemos multiplicar el vector de suma de E por 1/5, y así sucesivamente. .

Por lo tanto, al multiplicar D̃ inversa y X, podemos obtener el promedio de los vectores de características de todos los vecinos (incluido él mismo).

Hasta ahora, todo bien. Pero puede preguntar ¿Qué tal el promedio ponderado ()? Intuitivamente, debería ser mejor si tratamos los nodos de alto y bajo grado de manera diferente.

Echemos un vistazo más profundo al enfoque de promedio () que acabamos de mencionar. De la propiedad asociativa de la multiplicación de matrices, para cualesquiera tres matrices $\mathrm{A}$ , $\mathrm{B}$ y $\mathrm{C}$ ,( $\mathrm{A} B) \mathrm{C}=A(B \mathrm{C}$ . Más bien $\tilde{D}^{-1}(\tilde{A} X)$ , consideramos $\left(\tilde{D}^{-1} \tilde{A}\right) X$ , entonces $\tilde{D}^{-1}$ también puede verse como el factor de escala de $\tilde{A}$ . Desde esta perspectiva, cada fila i de $\tilde{A}$ será escalado por $\tilde{D}_{ii}$ (La siguiente figura). Nótese que $\tilde{A}$ es una matriz simétrica, significa que la fila i tiene el mismo valor que la columna i. Si escalamos cada fila i por $\tilde{D}_{ii}$ , intuitivamente, tenemos la sensación de que deberíamos hacer lo mismo para su columna correspondiente también.

Matemáticamente, estamos escalando $\tilde{A}_{ij}$ solo por $\tilde{D}_{ii}$ . Estamos ignorando el índice j. Entonces, ¿qué pasaría cuando escalamos $\tilde{A}_{ij}$ por ambos $\tilde{D}_{ii}$ y $\tilde{D}_{jj}$ ?

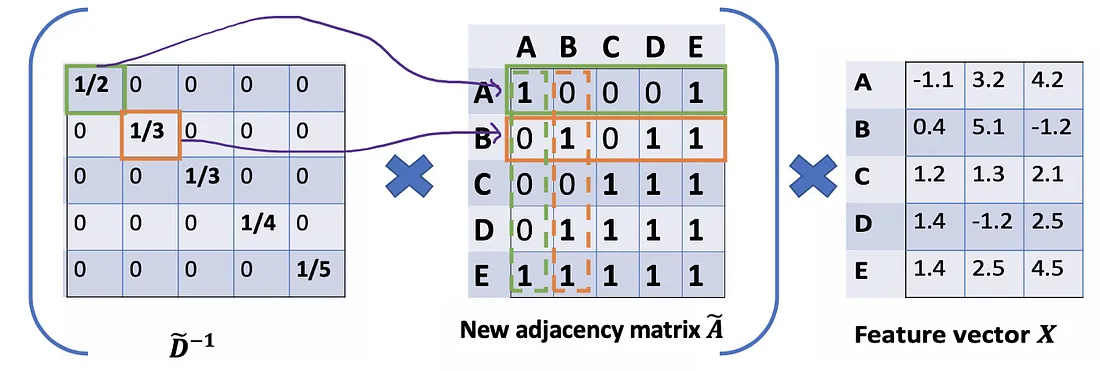
Solo estamos escalando por filas pero ignorando sus columnas correspondientes (cuadros de guiones)

Probamos una nueva estrategia de escalado: en lugar de usar $\tilde{D}^{-1}\tilde{A}X$ , usamos $\tilde{D}^{-1}\tilde{A}\tilde{D}^{-1}X$ . $_$

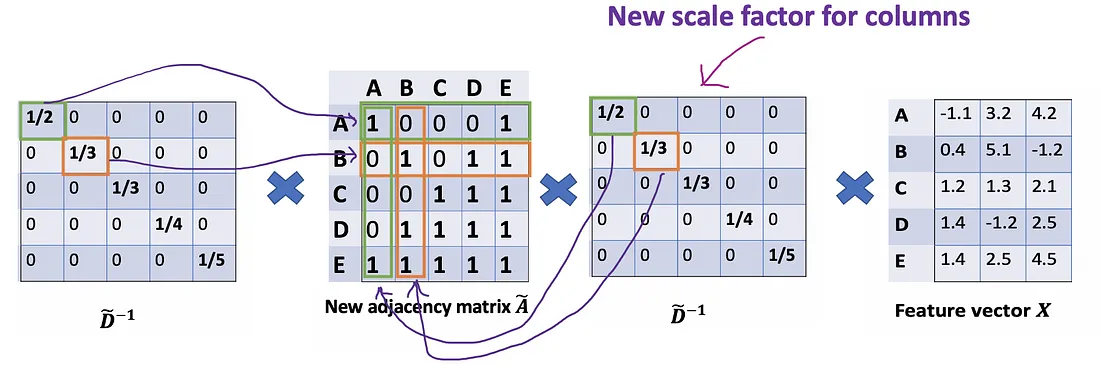
Agregue un nuevo escalador para columnas.

El nuevo escalador nos da el promedio "ponderado". Lo que estamos haciendo aquí es poner más peso en los nodos que tienen bajo grado y reducir el impacto de los nodos de alto grado. La idea de este promedio ponderado es que asumimos que los nodos de grado bajo tendrían un impacto mayor en sus vecinos, mientras que los nodos de grado alto generan impactos menores ya que dispersan su influencia en demasiados vecinos.

Al agregar características en el nodo B, asignamos el peso más alto para el nodo B en sí (grado de 3) y el peso más bajo para el nodo E (grado de 5)

Una nota menor más : cuando se usan dos escaladores ( $\tilde{D}_{ii}$ y $\tilde{D}_{jj}$ ), en realidad normalizamos dos veces , una vez para la fila como antes y otra vez para la columna. Tendría sentido si reequilibramos modificando $\tilde{D}_{ii}\tilde{D}_{jj}$ a $\sqrt {\tilde{D}_{ii}\tilde{D}_{jj}}$ ; En otras palabras, en lugar de usar $\tilde{D}^{-1}$ , usamos $\tilde{D}^{-1/2}$ . Entonces, modificamos aún más la fórmula a $\tilde{D}^{-1/2}\tilde{A}\tilde{D} ^{-1/2}X$ ,que se usa exactamente en el artículo.

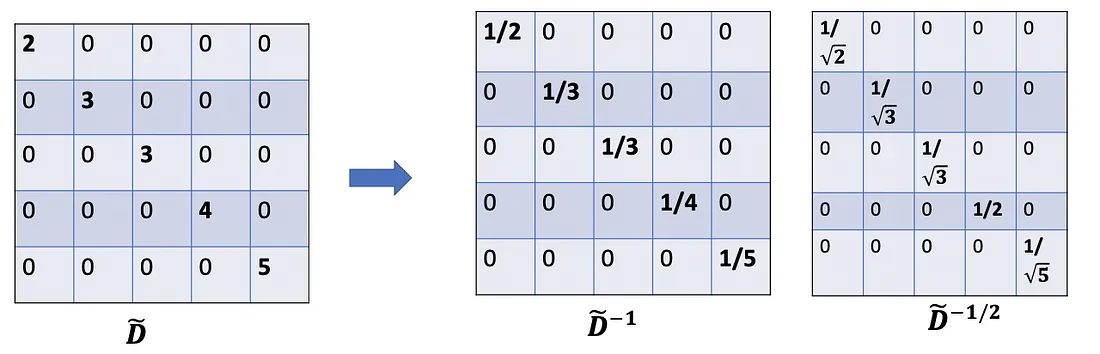
Debido a que normalizamos dos veces, cambiamos "-1" a "-1/2"

Resumen rápido hasta ahora :

$\tilde{A}X$ : suma de los vectores de características de todos los vecinos, incluido él mismo.
$\tilde{D}^{-1}\tilde{A}X{:}$ promedio de los vectores de características de todos los vecinos (incluido él mismo). La matriz de adyacencia se escala por filas.
$\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}X$ : promedio de los vectores de características de todos los vecinos (incluido él mismo). La matriz de adyacencia se escala tanto por filas como por columnas. Al hacer esto, obtenemos el promedio ponderado que prefiere los nodos de bajo grado.

Bien, ahora pongamos las cosas juntas .

Llamemos $\hat{A}=\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{- 1/2}$ solo para una vista clara. Con GCN de 2 capas, tenemos la forma de nuestro modo de avance como se muestra a continuación.

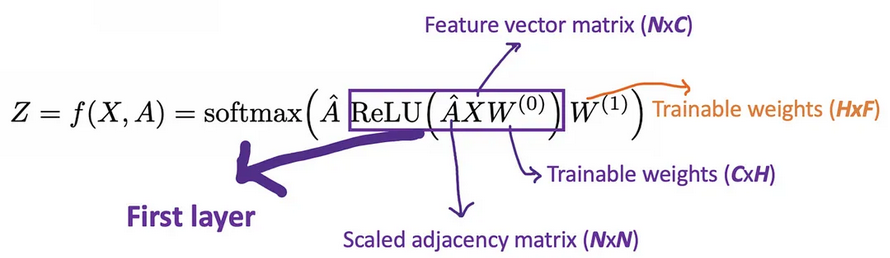
Recuerde que N es # nodos, C es # dimensiones de vectores de características. También tenemos His # nodos en la capa oculta y Fis las dimensiones de los vectores resultantes.

Por ejemplo, tenemos un problema de clasificación múltiple con 10 clases, F se establecerá en 10. Después de tener los vectores de 10 dimensiones en la capa 2, pasamos estos vectores a través de una función softmax para la predicción.

La función de pérdida se calcula simplemente por el error de entropía cruzada sobre todos los ejemplos etiquetados, donde Y_{l} es el conjunto de índices de nodo que tienen etiquetas.

$\mathcal{L}=-\sum_{l\in\mathcal{Y}_L}\sum_{f=1}^FY_{lf}\ en Z_{lf}$

El número de capas

El significado de #capas

El número de capas es la distancia más lejana que pueden viajar las entidades de nodo. Por ejemplo, con GCN de 1 capa, cada nodo solo puede obtener la información de sus vecinos. El proceso de recopilación de información se lleva a cabo de forma independiente, al mismo tiempo para todos los nodos.

Al apilar otra capa sobre la primera, repetimos el proceso de recopilación de información, pero esta vez, los vecinos ya tienen información sobre sus propios vecinos (del paso anterior). Hace que el número de capas sea el número máximo de saltos que cada nodo puede recorrer. Entonces, depende de qué tan lejos creamos que un nodo debe obtener información de las redes, podemos configurar un número adecuado para #capas. Pero de nuevo, en el gráfico, normalmente no queremos ir demasiado lejos. Con 6 o 7 saltos, casi obtenemos el gráfico completo, lo que hace que la agregación sea menos significativa.

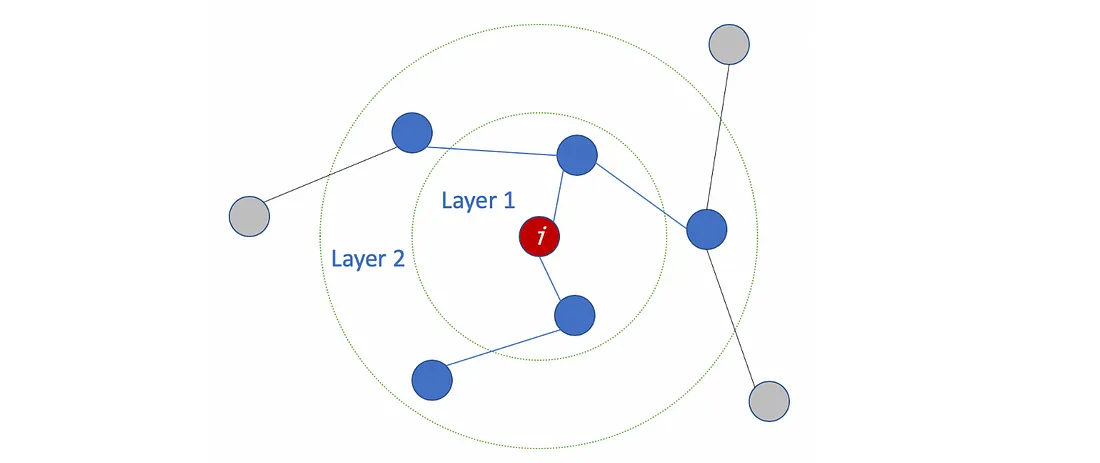
Ejemplo: proceso de recopilación de información con 2 capas del nodo de destino i

¿Cuántas capas debemos apilar el GCN?

En el documento, los autores también realizaron algunos experimentos con GCN superficiales y profundos. De la siguiente figura, vemos que los mejores resultados se obtienen con un modelo de 2 o 3 capas. Además, con un GCN profundo (más de 7 capas), tiende a tener malos rendimientos (línea azul discontinua). Una solución es utilizar las conexiones residuales entre capas ocultas (línea morada).

Rendimiento sobre #capas. Imagen del periódico [3]

Llevar notas a casa

Los GCN se utilizan para el aprendizaje semisupervisado en el gráfico.
Los GCN utilizan funciones de nodo y la estructura para el entrenamiento.
La idea principal de la GCN es tomar el promedio ponderado de las características de los nodos de todos los vecinos (incluido él mismo): los nodos de menor grado obtienen pesos más grandes. Luego, pasamos los vectores de características resultantes a través de una red neuronal para el entrenamiento.
Podemos apilar más capas para hacer que los GCN sean más profundos. Considere conexiones residuales para GCN profundos. Normalmente, optamos por GCN de 2 o 3 capas.
Nota matemática: cuando vea una matriz diagonal, piense en la escala de la matriz.
Una demostración de GCN con la biblioteca StellarGraph aquí [5]. La biblioteca también proporciona muchos otros algoritmos GNN. Además, DGL [7] es otra buena biblioteca para GNN. Si bien StellarGraph nos ayuda a configurar el modelo fácilmente, DGL tiene como objetivo proporcionar una estructura más flexible que resulta útil al personalizar nuestros modelos.

Nota de los autores del artículo.

Actualmente, el marco se limita a gráficos no dirigidos (ponderados o no ponderados). Sin embargo, es posible manejar tanto los bordes dirigidos como las entidades de borde representando el gráfico dirigido original como un gráfico bipartito no dirigido con nodos adicionales que representan bordes en el gráfico original.

En el documento, los autores presentan el proceso desde una perspectiva espectral, mientras que en esta publicación retrocedemos desde la fórmula de GCN para comprender cómo maneja el gráfico de entrada desde un punto de vista espacial.

¿Que sigue?

Con GCN, parece que podemos hacer uso tanto de las características del nodo como de la estructura del gráfico. Sin embargo, ¿qué pasa si los bordes tienen diferentes tipos? ¿Deberíamos tratar cada relación de manera diferente? ¿Cómo agregar vecinos en este caso? ( R-GCN )

Desde otra perspectiva, ¿cómo podemos mejorar aún más el modelo GCN? ¿El uso de pesos fijos que prefieren nodos de bajo grado es lo suficientemente bueno? ¿Hay alguna manera de que podamos dejar que el modelo aprenda los pesos automáticamente por sí mismo ( Graph Attention Networks )? ¿Cómo podemos lidiar con gráficos grandes que no pueden caber en la memoria a la vez, o usar agregadores más complejos ( GraphSAGE )?

En la próxima publicación sobre el tema de los gráficos, veremos algunos métodos GNN más sofisticados.

¿Cómo lidiar con diferentes relaciones en los bordes (hermano, amigo,….)?

REFERENCIAS

[1] Excelentes diapositivas sobre Graph Representation Learning de Jure Leskovec (Curso de Stanford — cs224w): http://web.stanford.edu/class/cs224w/slides/07-noderepr.pdf

[2] Redes convolucionales de gráficos de video (GCN) simplificadas: https://www.youtube.com/watch?v=2KRAOZIULzw

[3] Clasificación semisupervisada con redes convolucionales gráficas (2017): https://arxiv.org/pdf/1609.02907.pdf

[4] Código fuente de GCN: https://github.com/tkipf/gcn

[5] Demostración con la biblioteca StellarGraph: https://stellargraph.readthedocs.io/en/stable/demos/node-classification/gcn-node-classification.html

[6] Una encuesta completa sobre redes neuronales gráficas (2019): https://arxiv.org/pdf/1901.00596.pdf

[7] Biblioteca DGL: https://docs.dgl.ai/guide/graph.html

【Reimpresión】Graph Convolucional Networks (GCN)