1. What fractal
Fractal, having the morphological characteristic of filling space with non-integer dimensions. It is usually defined as "a rough or fragmented geometric shape that can be divided into several parts, and each part is (at least approximately) the reduced shape of the whole", that is, it has the property of self-similarity. A more formal definition is: a collection in which the part and the whole are similar in some way. Fractal properties include self-similarity, scale invariance, fractal dimensionality and so on. Fractal (Fractal) is a word, Mandelbrot (derived from the Latin adjective fractus, the corresponding Latin verb is frangere ("broken", "to produce random fragments"), and the English fraction ("fragments", " Score") and fragment ("fragment") have the same root. Before the mid-1970s, Mundbro had been using the word fractional in English to express his fractal thought, so he took the head of the Latin word and the tail of the English word) The created word (fract+al=fractal) originally meant to be irregular, broken, and fractional.
The translation of Mandelbrot in the Chinese literature has not been uniform. Mandelbrot was approved by the National Science and Technology Terms Approval Committee in 2019 and approved by the Mandelbrot set [collection] (Mandelbrot set). Translated into Mandelbrot, Mandelbrot, etc., the Chinese name used by Mandelbrot himself is "Benhua Mandelbrot" (see Figure 1). Mandelbrot (1924-2010) French original Benoît B. Mandelbrot, English name Benoit B. Mandelbrot.

Figure 1 Benoît B.Mandelbrot and his Chinese signature
In 1973, Mandelbrot first proposed the idea of fractal dimension and fractal when he was lecturing at the Collège de France. Fractal theory is a very popular and active new theory and new subject in today's world. The concept of fractal was first proposed by the American mathematician Mundbro. In 1967, he published a famous paper entitled "How long is the coastline of Britain?" (How long is the coastline of Britain) in the American authoritative "Science" magazine. As a curve, the coastline is characterized by extremely irregular, extremely rough, and presents extremely meandering and complex changes. In fact, forms with self-similarity widely exist in nature, such as: continuous mountains and rivers, floating clouds, rock fractures, the trajectory of Brownian particles, tree crowns, cauliflower, cerebral cortex..., Mundbro put Shapes whose parts resemble the whole in some way are called fractals. As shown in Fig. 2, Roman cauliflower, any upper small flower (partial) on it is still a very similar shape of the whole vegetable (overall) after being enlarged.


(a) Whole cauliflower (b) Local enlargement
Figure 2 Roman cauliflower, discovered in Italy in the 16th century
In 1975, Mandelbrot founded fractal geometry. On this basis, the science of studying fractal properties and its applications is formed, which is called fractal theory.
Closed fractal graphics have the characteristics of finite area and infinite perimeter.
2. What is recursion and recursive algorithm
1. Recursion
An object is said to be recursive if it partially consists of itself, or defines itself. Recursion is encountered not only in mathematics, but also in daily life (as shown in Figure 3).

Figure 3 Recursion diagram in daily life ( two parallel plane mirrors produce infinite images)
2. Recursive Algorithm
An algorithm that calls itself directly or indirectly is called a recursive algorithm. A function that calls a function itself is called a recursive function.
A recursive algorithm in computer science refers to a method of solving a problem by repeatedly decomposing it into subproblems of the same kind. Recursive methods can be used to solve many computer science problems, so it is a very important concept in computer science.
3. Python draws fractal graphs
In Python, a recursive algorithm (recursive function) can be used to draw a fractal diagram using turtle (sea turtle).
1. Koch curve
The construction process of the Koch curve is mainly divided into three steps: (1) Given an initial figure—a line segment; (2) Replace the middle 1/3 length of this line segment with a bottomless equilateral triangle of this length ( See Fig. 4 (b)); (3) constantly replace the 1/3 length in the middle of each segment line segment with a bottomless equilateral triangle of this length according to the method of the second step. Going on indefinitely like this, the Koch curve (as shown in Figure 4) can be constructed finally. The straight line segment is called the 0th-order Koch curve, after one replacement, it is called the 1st-order Koch curve, and each straight line segment of the 1st-order Koch curve is replaced once again, then it is called the 2nd-order Koch curve. Add 1, in Figure 4 (a) is a straight line (0th order), (b) is a 1st order curve, (c) is a 2nd order curve, (d) is a 3rd order curve, (e) is a 4th order curve, (f ) is a curve of degree 5. Obviously this is a recursive process.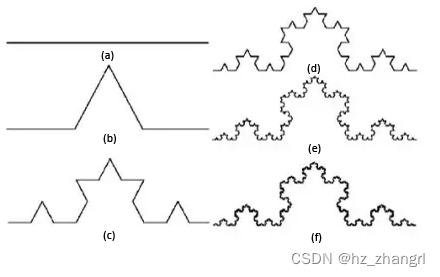
Figure 4 Koch curve _
2. Draw the Koch curve with Python
It can be seen from Figure 4(b) that if the length of the straight line in Figure 4(a) is l, then turn left 0° (equal to no turning) and draw a l/3 long straight line forward, turn left 60° and draw a l/3 long straight line forward , turn right 120 ° (i.e. turn left -120 °) and draw a 1/3 long straight line forward, turn left 60 ° and draw a 1/3 long straight line forward. It can be seen from Figure 4(c) that if the length of the straight line in Figure 4(b) is l, then the above-mentioned drawing rules can be repeated for drawing. This is a recursive problem. Each straight line is completed with 4 actions of turning left + drawing a straight line of a specified length forward, each drawing with 1/3 of the previous length until the 0th order.
Python uses turtle to draw the Koch curve program code as follows:

The running results are shown in Figure 5.
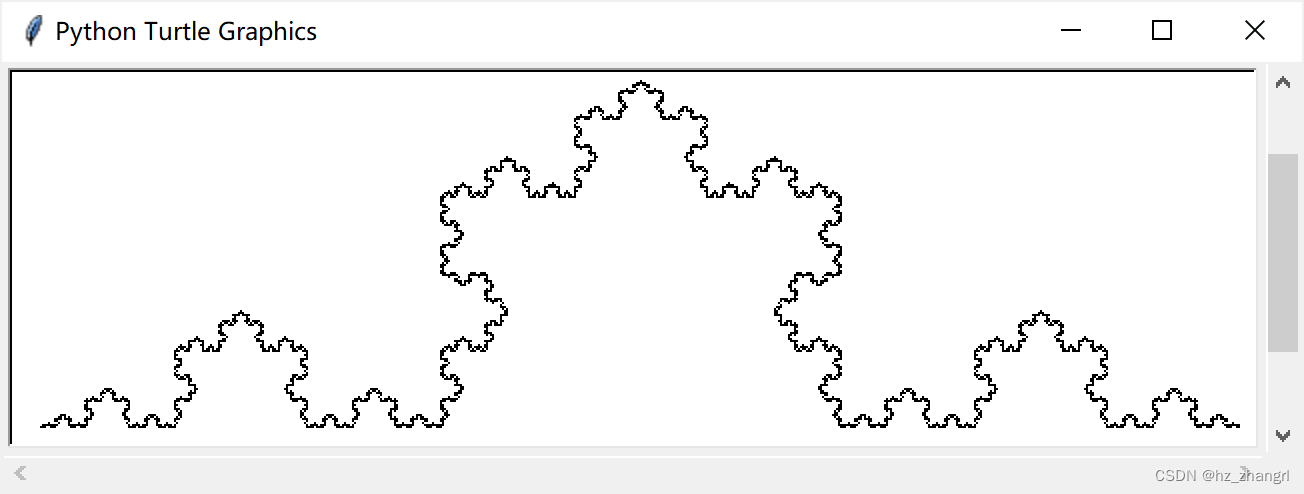
Figure 5 6th order Koch curve
3. Koch snowflakes
As shown in Figure 6(a), an equilateral triangle whose side length is l, takes one-third of the middle of each side, and then connects it with a completely similar shape but whose side length is one-third the triangle without the base, The result is a hexagon (Fig. 6(b)). Take each side of the hexagon and do the same transformation, that is, connect a smaller triangle with the base removed in the middle third (Fig. 6(c)), and repeat until infinity. The edges become more finely zigzag, and the shape approaches an idealized snowflake (Fig. 6(d)).
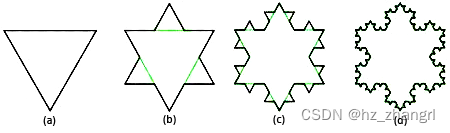
Figure 6 Schematic diagram of Koch snowflake generation
4. Drawing Koch Snowflakes with Python
As shown in Figure 6(a), an equilateral triangle with a downward side length l, each side is drawn according to the Koch curve, that is, each of the three sides is drawn once according to the Koch curve, and a Koch snowflake can be obtained.
Python uses turtle to draw Koch snowflake program code as follows:

The running result is shown in Figure 7.

Figure 7 4th order Koch snowflake
5. Fractal binary tree
If you draw a line segment upward, draw a shorter line to the left and right at the end point, draw a shorter line to the left and right at the end point, and so on, you can draw a binary tree. The first line is the trunk, and the others are branches, which terminate when the length of the line (branch) shortens to a certain length. This is also a typical recursive algorithm.
Python uses turtle to draw fractal binary tree program code as follows:
'''绘制分形二叉树'''
import turtle as tl
def draw_branches(tree_length,tree_angle):
'''绘制分形二叉树递归函数'''
if tree_length >= 5: # 树枝长小于5则结束
tl.forward(tree_length) # 往前画树杆、树枝
tl.right(tree_angle) # 往右转(先画右侧树枝)
draw_branches(tree_length * 0.75,tree_angle) # 画下一枝,树枝长降25%
tl.left(2 * tree_angle) # 转向画左,画左侧树枝
draw_branches(tree_length * 0.75,tree_angle) # 画下一枝,树枝长降25%
if tree_length <= 10: # 树枝长小于10,可以当作树叶
tl.pencolor('green') # 树叶部分为绿色
else:
tl.pencolor('brown') # 树干部分为棕色
tl.rt(tree_angle) # 回正到上一枝方向
tl.backward(tree_length) # 然后往回画,回溯到上一层继续画
if __name__ == '__main__':
tl.up()
tl.speed(0)
tl.lt(90) # 因为树是往上的,所以先把方向向上
tl.bk(200) # 把起点放到树干底部
tl.pd()
tl.pencolor('brown') # 树干部分为棕色
tree_length = 100 # 设置树干的初始长度为100
tree_angle = 20 # 树枝分叉角度40°,左右各20°
draw_branches(tree_length,tree_angle) # 启动绘图
tl.exitonclick() # 点击退出绘图窗口
The running result is shown in Figure 8. Due to the self-similarity of fractals, this binary tree is completely symmetrical. When drawing, a line thickness is used, and the trunk looks too thin, not quite like a tree.
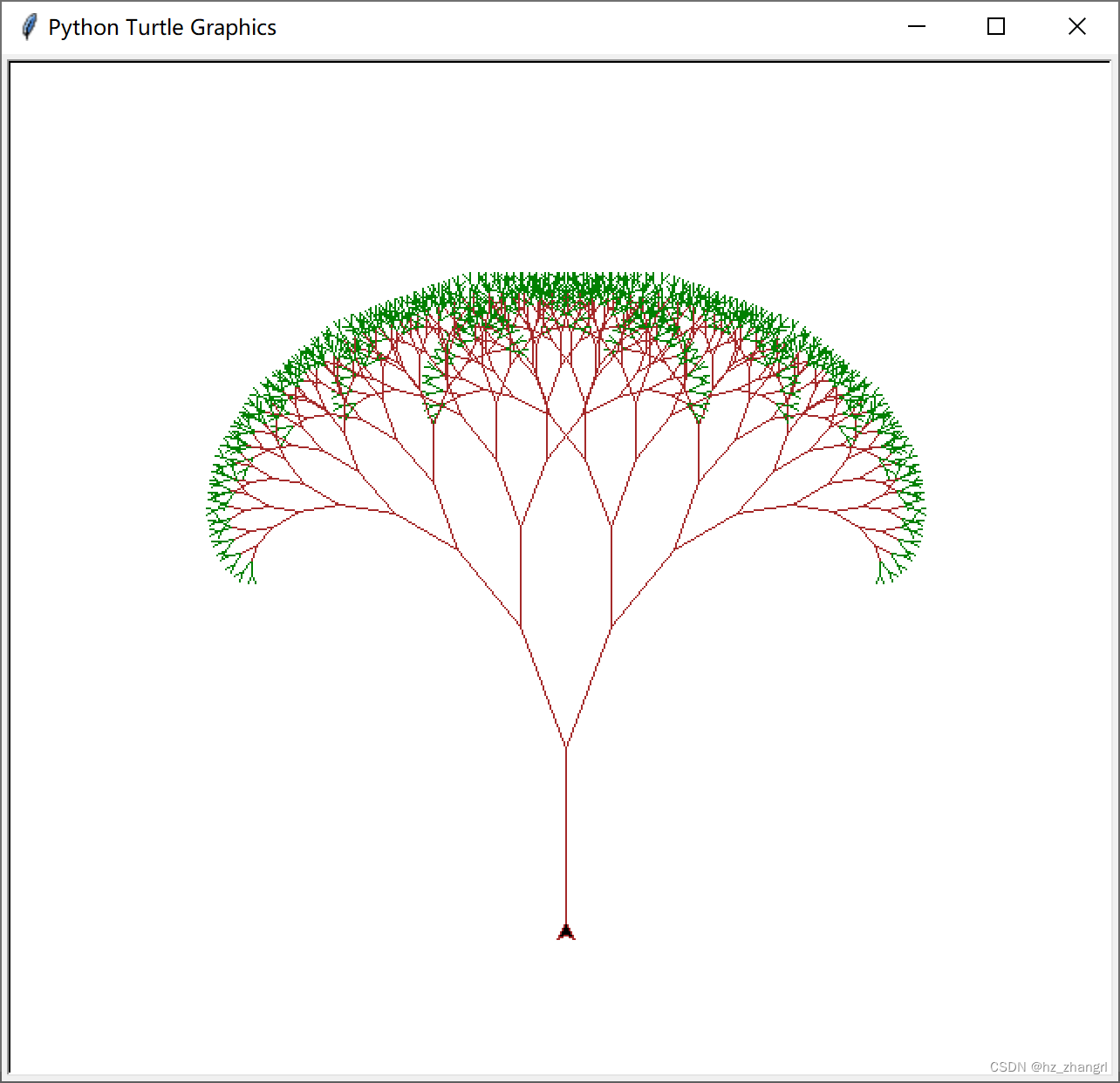
Figure 8 Simple fractal binary tree
6. Fractal binary tree with trunk and branch thickness change
If on the basis of drawing a fractal binary tree, let the trunk and branches become thinner in proportion (also available in arithmetic difference), and thicken the brush when drawing the last line near the end, the last leaves (leaf nodes) will be smaller than the branches Thick and more like leaves, then more like a tree.
Python uses turtle to draw the fractal binary tree program code of trunk and branch thickness change as follows:
'''绘制树干树枝放粗细变化的分形二叉树'''
import turtle as tl
def draw_branches(tree_length, tree_size, tree_angle):
'''
绘制树干树枝放粗细变化的分形二叉树递归函数
'''
tl.pensize(tree_size)
if tree_length >= 5: # 树枝长小于5则结束
tl.forward(tree_length) # 往前画树杆、树枝
tl.right(tree_angle) # 往右转(先画右侧树枝)
# 画右下一枝,树枝长降25%,粗细降15%
draw_branches(tree_length * 0.75, tree_size * 0.85, tree_angle)
tl.left(2 * tree_angle) # 往左转(再画左侧树枝)
# 画左下一枝,树枝长降25%,粗细降15%
draw_branches(tree_length * 0.75, tree_size * 0.85, tree_angle)
if tree_length <= 10: # 树枝长小于10,可以当作树叶 tl.pencolor('green')
tl.pencolor('green') # 树叶部分为绿色
if tree_length <= 7: # 树尖端部分
tl.pensize(3) # 让树叶宽一点
else:
tl.pensize(tree_size) # 非树叶原粗细
else:
tl.pencolor('brown') # 树干部分为棕色
tl.rt(tree_angle) # 回正到上一枝方向
tl.backward(tree_length) # 然后往回画,回溯到上一层继续画
if __name__ == '__main__':
tl.penup()
tl.speed(0)
tl.left(90) # 因为树是往上的,所以先把方向转上
tl.backward(200) # 把起点放到底部
tl.pendown()
tl.pencolor('brown') # 树干部分为棕色
tree_length = 100 # 设置的树干最长为100
tree_size = 6 # 设置的最粗树干为6
tree_angle = 20 # 树枝分叉角度40°,左右20°
draw_branches(tree_length, tree_size, tree_angle) # 启动绘图
tl.exitonclick() # 点击退出绘图窗口The running result is shown in Figure 9. Due to the self-similarity of fractals, the tree is completely symmetrical and relatively rigid, but it is more like a tree than Figure 8.
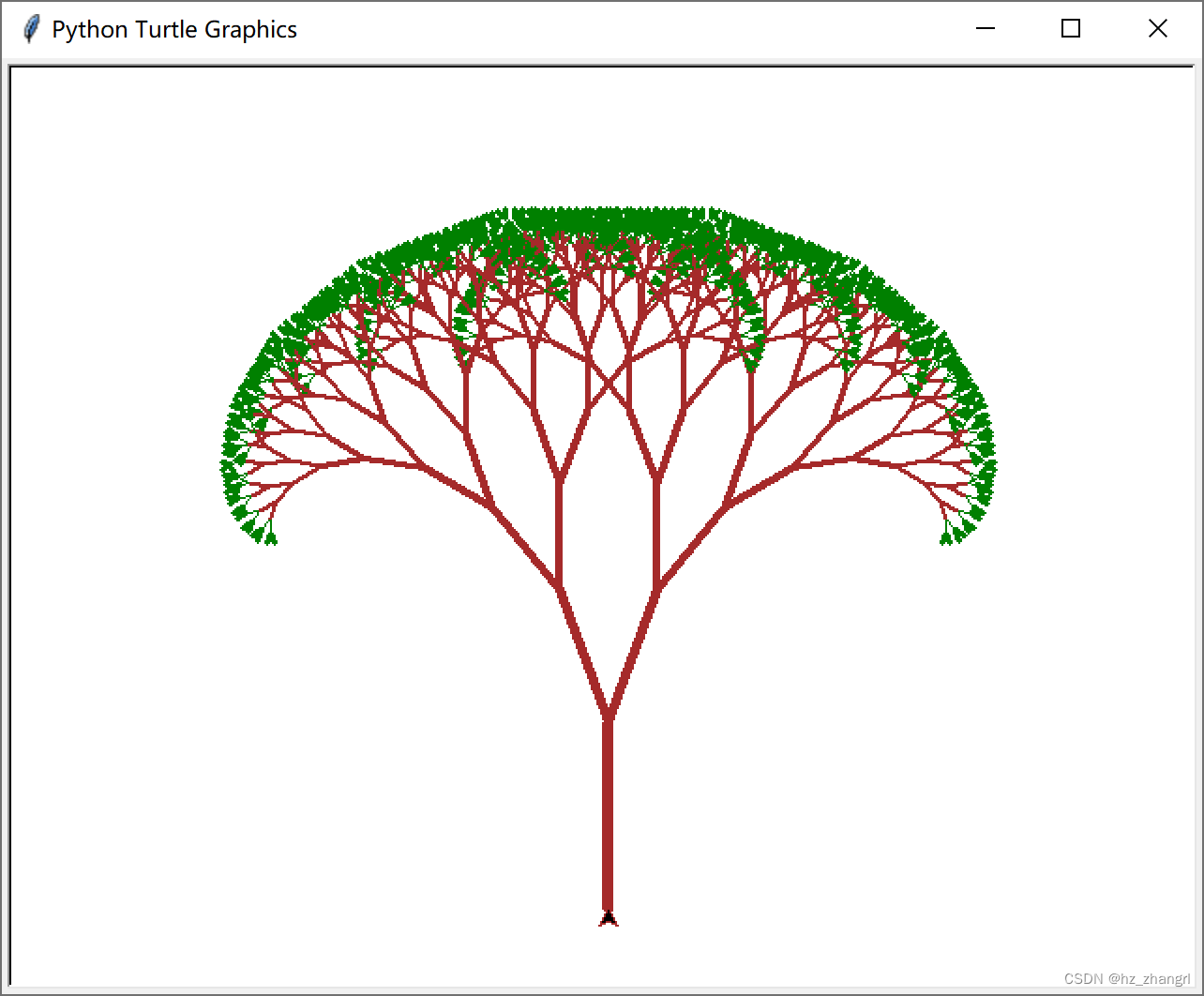
Figure 9 Fractal binary tree with trunk and branch thickness changes
If random number perturbation is added to the length of the trunk and branches, and the angle between branches is also added to the random number perturbation, it will be more like a natural tree, because the space is too long to be discussed in the next article.