算法笔记——3动态规划

动态规划

动态规划自下而上解决问题，每个子问题都必须求解。

动态规划的两个特性：

1、子问题不相互独立。
2、具有最优子结构性。

典型问题：

1、矩阵连乘

给定n个矩阵｛A1,A2,…,An｝，其中，Ai与Ai+1是可乘的，(i=1,2 ,…,n-1)。用加括号的方法表示矩阵连乘的次序，不同的计算次序计算量（乘法次数）是不同的，找出一种加括号的方法，使得矩阵连乘的次数最小。

例如：
A1是A（5* 10）的方阵；
A2是A（10 * 100）的方阵；
A3是A（100 * 2）的方阵；

那么有两种加括号的方法：

1.（A1A2）A3；
2. A1（A2A3）；

第一种方法的计算量：5 * 10 * 100+5 * 100 * 2=6000；
第二种方法的计算量：10 * 100 * 2+5 * 10 * 2=2100；
可以看出不同计算方法计算量差别很大。



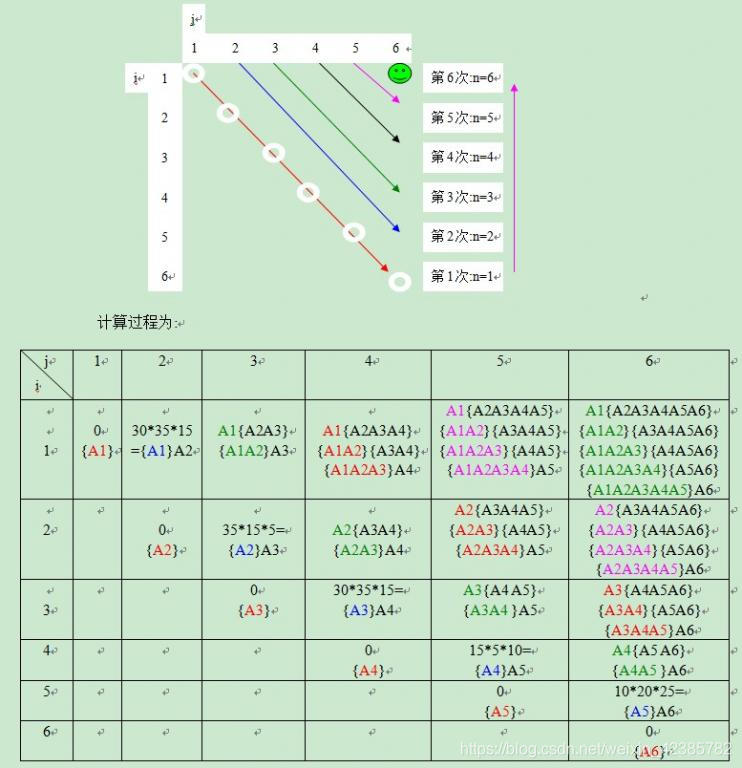
根据表格可得到最优值，但不知道最优解。
求最优解，需要开一个S[][]数组记录断点。
算法的时间复杂度为O（n的3次方）

2、最长公共子序列

给定两个字符串，求解这两个字符串的最长公共子序列（Longest Common Sequence）。比如字符串1：BDCABA；字符串2：ABCBDAB
则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

由一下三种情况：
1、C[I,J]=0
2、当前两个字符串的最后一个字符相同，则该 字符必在这两个字符串的相同公共子序列中。
3、若当前两个字符串的最后一个字符不同，则在C[I,J-1]和C[I-1,J]中选择一个最大的。

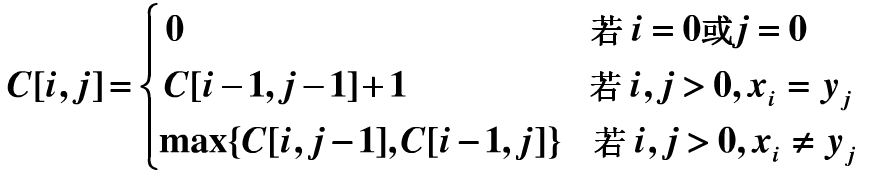
时间复杂度为 o(nm)

3、图像压缩

图像压缩的问题我们是这样理解的：大家都知道计算机的图像是用灰度值序列来表示的｛P1,P2…Pn｝,其中Pi表示像素点i的灰度值。而通常灰度值的范围是0~255，因此需要8位二进制数来表示一个像素。这个时候大家应该有了一些小的疑问：我能不能用更少的位数来表示灰度值？（因为有的灰度值并没有达到255这么大）所以我们引入了图像压缩算法来解决这个问题。

其中开头的声明长度为11
递推公式：


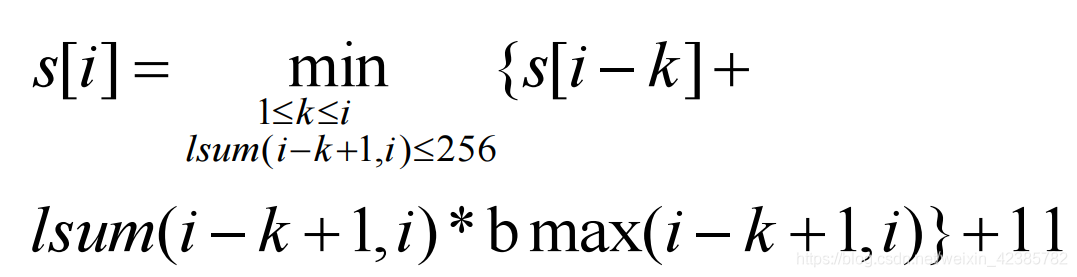
时间复杂度为O(n)

4、流水作业调度

n个作业{1，2，…，n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。流水作业调度问题要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少。

时间复杂度为（nlogn)

5、0-1背包

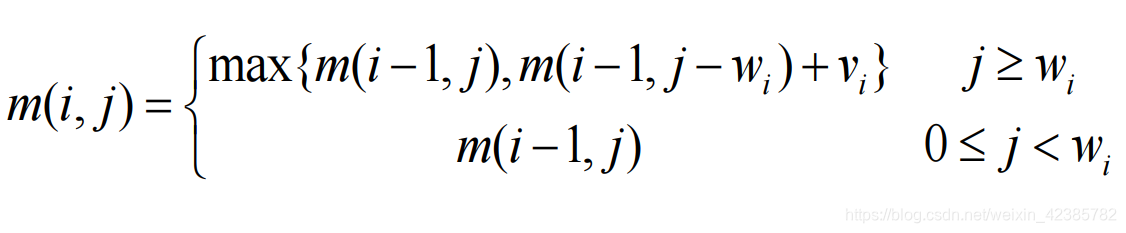
#include<iostream>
#include <iomanip>
using namespace std;
#include <algorithm>
int input[4][3] = { 1, 2, 12,
					2, 1, 10,
					3, 3, 20,
					4, 2, 15};
int w[5] = { 0 };		
int v[5] = { 0 };//价值			
int bagV = 15;					        
int dp[5][16] = { { 0 } };			       
int item[5];

//初始化
void start() 
{
	for (int i = 0;i <= 3;i++) 
	{
		v[i + 1] = input[i][2];
		w[i + 1] = input[i][1];
	}
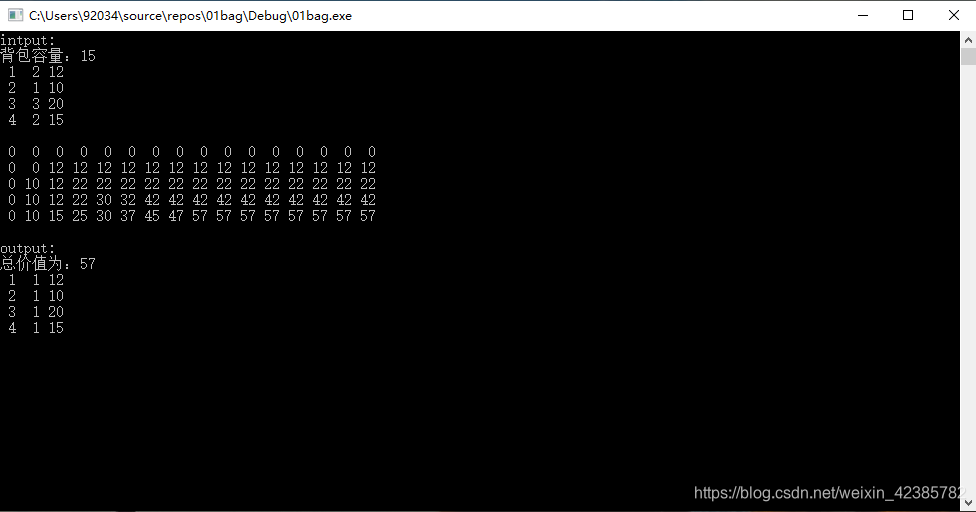
	cout << "intput:" << endl;
	cout << "背包容量：" << bagV << endl;
	for (int i = 0; i <= 3; i++) {			
		for (int j = 0; j <= 2; j++) {
			cout << setw(2) << input[i][j] << ' ';
		}
		cout << endl;
	}
	cout << endl;
}

//动态规划
void findMax() {				
	for (int i = 1; i <= 4; i++) {
		for (int j = 1; j <= bagV; j++) {
			if (j < w[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	}
}

//寻找最优解
void findWhat(int i, int j) {			
	if (i > 0) {
		if (dp[i][j] == dp[i - 1][j]) {
			item[i] = 0;
			findWhat(i - 1, j);
		}
		else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
			item[i] = 1;
			findWhat(i - 1, j - w[i]);
		}
	}
}

void print() {
	for (int i = 0; i < 5; i++) {			
		for (int j = 0; j < 16; j++) {
			cout <<setw(2)<<dp[i][j] << ' ';
		}
		cout << endl;
	}
	cout << endl;

	cout<<"output:"<<endl;

	cout <<"总价值为："<< dp[4][bagV] << endl;

	for (int i=0;i<=3;i++) 
	{
		input[i][1] = item[i+1];
	}

	for (int i = 0; i <=3; i++) {			
		for (int j = 0; j <=2; j++) {
			cout <<setw(2)<<input[i][j] << ' ';
		}
		cout << endl;
	}
	cout << endl;
}

int main()
{
	start();
	findMax();
	findWhat(4, bagV);
	print();
	getchar();
	return 0;
}

算法复杂度O（n2的n次方）