智能合约隐私保护技术之同态加密

1.同态加密简介

1.1.定义

同态加密(Homomorphic Encryption)是一种特殊的加密方法，允许对密文进行处理得到仍然是加密的结果。即对密文直接进行处理，跟对明文进行处理后再对处理结果加密，得到的结果相同。从抽象代数的角度讲，保持了同态性。

同态加密是基于数学难题的计算复杂性理论的密码学技术，它的概念可以简单的解释为：对经过同态加密的数据进行密文运算处理得到一个输出，这一输出解密结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。

同态加密可以保证实现处理者无法访问到数据自身的信息。如果定义一个运算符Δ，对加密算法E和解密算法D，满足：E(XΔY)=E(X)ΔE(Y)则意味着对于该运算满足同态性。

同态性来自代数领域，一般包括四种类型：加法同态、乘法同态、减法同态和除法同态。同时满足加法同态和乘法同态，则意味着是代数同态，称为全同态(Full Homomorphic)。同时满足四种同态性，则称为算数同态。

对于计算机操作来讲，实现了全同态意味着对于所有处理都可以实现同态性。只能实现部分特定操作的同态性，称为特定同态(Somewhat Homomorphic)。对于特定同态特性的算法，如RSA，Elgamal，Paillier、Pedersen Commitment等等。

1.2.作用

同态加密首先运用在云计算和大数据中。对于区块链技术，同态加密也是很好的互补。使用同态加密技术，运行在区块链上的智能合约可以处理密文，而无法获知真实数据，极大地提高了隐私安全性。

对于区块链网络用户来说，希望提交到区块链网络中的数据安全性能得以保证，尤其是重要敏感数据的安全性，应避免恶意的信息泄露和篡改。同态加密技术能够使用户的密文数据在区块链智能合约中密文运算，而非传统的明文运算。这样的优点是，用户将交易数据提交到区块链网络之前，可使用相应的加密算法对交易数据进行加密，数据以密文的形式存在，即使被攻击者获取，也不会泄露用户的任何隐私信息，同时密文运算结果与明文运算结果一致。

2.业界使用同态加密

华为区块链提供同态加密库，对用户的交易数据用其公钥进行加密保护，交易的时候都是密文运算，最终账本中加密保存，即使节点被攻破，获取到账本记录也无法解密。

趣链Hyperchain通过同态加密（采用Paillier同态加密算法）的加密思想实现区块中交易金额和账户余额的加密。其白皮书声称经过同态加密的交易验证时间约为10微秒，可以满足Hyperchain每秒上万笔交易的需求。

BCOS也采用了Paillier同态加密算法，并开源出了加法同态解说使用说明[1]，以及Paillier同态加密算法JAVA版实现[2]。当然还有其他产品，此处不再一一列举。

3.同态加密实现

3.1.Paillier加法同态加密算法

Paillier加密算法[3]是1999年Paillier发明的基于复合剩余类的困难问题的加法同态加密算法
（1）秘钥生成

• 随机选择两个大质数p和q满足 $gcd(pq, (p−1)(q−1))=1$。这个属性是保证两个质数长度相等。gcd即求两个数的最大公约数。
• 计算 $n=pq$和 $λ=lcm(p−1, q−1)$。lcm即求两个数的最小公倍数。
• 选择随机整数g， $g \in Z_{n^2}^*$，使得。此处定义 $L(x)=(x-1)/n$。
• 计算 $u={L(g^λmodn^2)}^{-1}modn$
• 公钥为(n, g)，私钥为(λ, μ)。

（2）加密

• 明文m，0≤m≤n。
• 选择随机数r，0<r<n， $g \in Z_{n^2}^*$，且 $gcd(r, n)=1$。
• 加密结果： $c=g^m*r^nmodn^2$

（3）解密
解密结果： $m={L(c^λmodn^2)}*u modn$

（4）同态属性

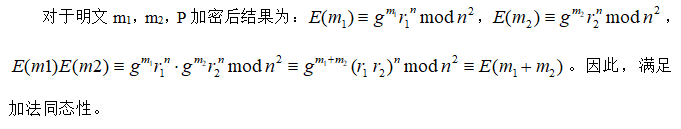
另外，对于任意的 $m_1，m_2 \in Z_n,k\in N$，Paillier密码体制还具有以下同态性质。

• $D(E(m)^{k}modn^2)=kmmodn$
• $D(E(m_1)g^{m_2}modn^2)=m_1+m_2modn$
• $D(E(m_1)^{m_2}modn^2)=m_1m_2modn$

（5）工程应用
Paillier算法既然是密文计算，必然会产生秘钥，因此工程应用时要提供秘钥管理机制，如秘钥创建、保存、颁发、撤销或销毁等。具体工程实现，可参考[2]，其中为提高计算速度，代码中使用了以下大数乘方取模优化（同余定理）：

• (A^E)%N = ((A%N)^E)%N
• (AB)%N = ((A%N)(B%N))%N
• (A +/- B) % C = (A % C +/- B % C) % C

3.2.ElGamal乘法同态加密算法

ELGamal密码是除了RSA之外最有代表性的公开密钥密码之一，它的安全性建立在离散对数问题的困难性之上，是一种公认安全的公钥密码。

离散对数问题
设p为素数，若存在一个正整数α，使得 $α、α^2、...、α^{p-1}$关于模p互不同余，则称α为模p的一个原根。于是有如下运算：

• α的幂乘运算： $y=α^x(mod p)$，1≤x≤p-1
• α的对数运算： $x=log_ay$，1≤y≤p-1

只要p足够大，求解离散对数问题时相当复杂的。离散对数问题具有较好的单向性。

(1)秘钥生成

• 随机地选择一个大素数p，且要求p-1有大素数因子，将p公开。
• 选择一个模p的原根α，并将α公开。
• 随机地选择一个整数d（1＜d＜p-1）作为私钥，并对d保密。
• 计算公钥 $y=α^d(mod p)$，并将y公开。

(2)加密

• 对于待加密明文M，随机地选取一个整数k（1＜k＜p-1）。

• 计算 $U=y^kmod p$、 $C_1=α^kmod p$、 $C_2=U*Mmod p$。

• 取 $(C_1,C_2)$作为密文。

(3)解密

(4)同态属性

4.引用

[1]https://github.com/bcosorg/bcos/blob/master/doc/manual/manual.md
[2]https://github.com/FISCO-BCOS/paillier-lib
[3]Paillier p. Public-key cryptosystems based on composite degree residuosity classes