五大常见算法策略之回溯策略

回溯策略

回溯是五大常用算法策略之一，它的核心思想其实就是将解空间看作是一棵树的结构，从树根到其中一个叶子节点的路径就是一个可能的解，根据约束条件，即可得到满足要求的解。求解问题时，发现到某个节点而不满足求解的条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。下面通过几个例子来讨论这个算法策略。

货郎问题

有一个推销员，要到n个城市推销商品，他要找出一个包含所有n个城市的具有最短路程的环路。（最后回到原来的城市），也就是说给一个无向带权图G<V,E>,用一个邻接矩阵来存储两城市之间的距离（即权值），要求一个最短的路径。

我们设置一组数据如下：4个城市，之间距离如下图所示，默认从0号城市出发

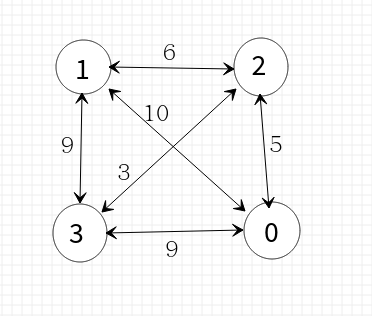
由此我们可以画出一棵解空间树：（只画了一部分，右边同理）

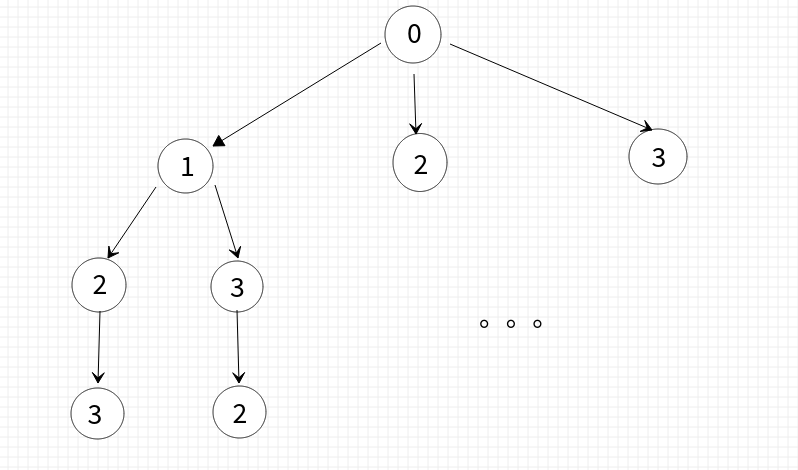
按照这个解空间树，对其进行深度优先搜索，通过比较即可得到最优结果（即最短路径）

package BackTrack;
//解法默认从第0个城市出发，减小了问题难度，主要目的在于理解回溯策略思想
public class Saleman {
    
    //货郎问题的回溯解法
    static int[][] map = {
            { 0,10,5,9},
            {10,0,6,9},
            { 5,6,0,3},
            { 9,9,3,0}
    };          //邻接矩阵
    
    public static final int N = 4;      //城市数量
    static int Min = 10000;             //记录最短的长度
    static int[] city = {1,0,0,0};      //默认第0个城市已经走过
    static int[] road = new int[N];     //路线，road[i] = j表示第i个城市是第j个经过的
    /**
     * 
     * @param city      保存城市是否被经过，0表示未被走过，1表示已经走过
     * @param j         上一层走的是第几个城市
     * @param len       此时在当前城市走过的距离总和
     * @param level     当前所在的层数，即第几个城市
     */
    public static void travel(int[] city, int j, int len, int level) {
        if(level == N - 1) {    //到达最后一个城市
            /*do something*/
            if(len+map[j][0] < Min) {
                Min = len + map[j][0];
                for (int i = 0; i < city.length; i++) {
                    road[i] = city[i];
                }
            }
            return;
        }
        for(int i = 0; i < N; i++) {
            if(city[i] == 0 && map[j][i] != 0) {    //第i个城市未被访问过，且上一层访问的城市并不是此城市
                city[i] = level+2;          //将此城市置为已访问
                travel(city, i, len+map[j][i], level+1);
                city[i] = 0;            //尝试完上一层的路径后，将城市又置为未访问，以免影响后面的尝试情况，避免了clone数组的情况，节省内存开销
            }
        }
        
    }
    
    public static void main(String[] args) {
        travel(city,0,0,0);
        System.out.println(Min);
        for (int i = 0; i < N; i++) {
            System.out.print(road[i]+" ");
        }
        System.out.println("1");
    }
}

八皇后问题

要在n*n的国际象棋棋盘中放n个皇后，使任意两个皇后都不能互相吃掉。规则：皇后能吃掉同一行、同一列、同一对角线的任意棋子。求所有的解。n=8是就是著名的八皇后问题了。

  用一个position数组表示皇后的摆放位置，position[i] = j表示第i行皇后放在第j列，我们从第一行开始，对每一列进行尝试摆放，如果可行则继续第二行，同理第二行继续对每一列进行尝试，如果发现某一行不管放在哪一列都不可行，说明上面某行的摆放是不可行的，则回溯到上面一行，从摆放的那一列接着往下尝试......

  这道题的解空间树非常庞大，第一层8个节点，然后往下每一个节点又有8个孩子（包含了所有可行和不可行解，但都要尝试过去），所以有8^8种可能解。

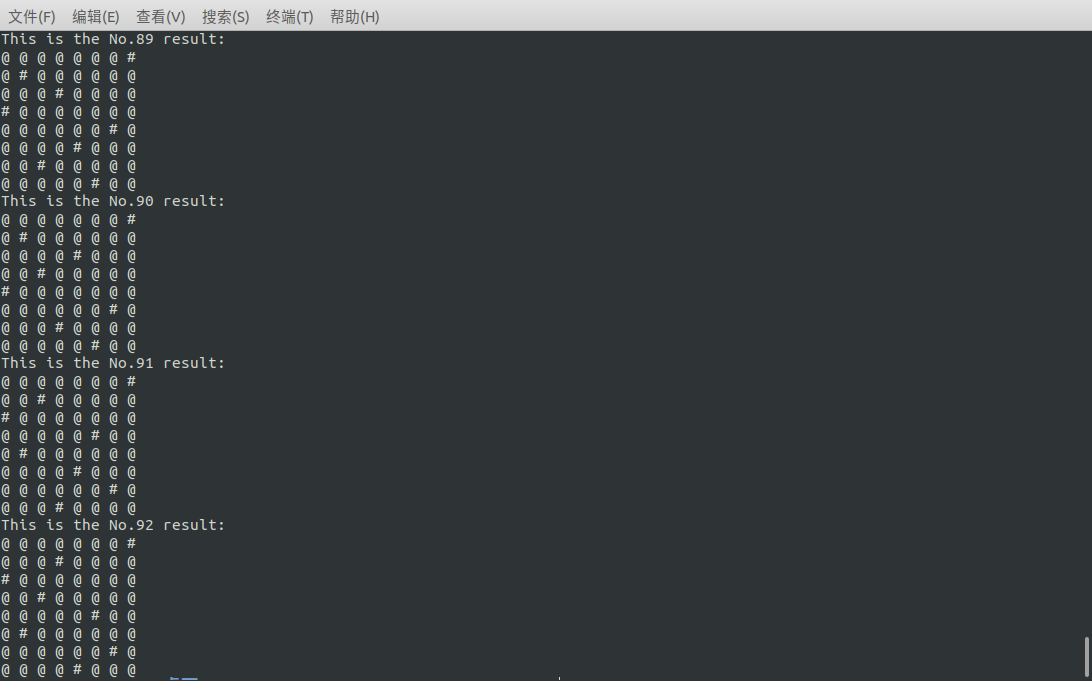
public class Empress {
    final static int N = 8;                   //皇后个数
    static int count = 0;                    //输出的结果个数
    static int[] postion = new int[N];      //保存每一行皇后摆放的位置，position[i] = j表示第i行皇后放在第j列

    /**
     * @param row   判断第row行摆放是否合理
     * @return      合理返回true，否则false
     */
    public static boolean IsOk(int row){
        for (int i = 0; i < row; i++) {     //和前面的每一行进行对比
            if(postion[i] == postion[row] || Math.abs(i-row) == Math.abs(postion[i] - postion[row])){
                //如果在同一列则postion[i] == postion[row]
                //如果在同一斜线上Math.abs(i-row) == Math.abs(postion[i] - postion[row])
                return false;
            }
        }
        return true;
    }

    public static void Print(){
        System.out.println("This is the No."+(++count)+" result:");
        for (int i = 0; i < N; i++) {           //i为行序号
            for (int j = 0; j < N; j++) {       //j为第i行皇后的列的序号
                if(postion[i] == j){    //不是皇后的拜访地址
                    System.out.print("# ");
                }else{
                    System.out.print("@ ");
                }
            }
            System.out.println();       //换行
        }
    }

    /**
     * @param row   尝试第row行皇后的摆放位置，找到可行位置就继续深度搜索下一行，否则在尝试完i的所有取值无果后回溯
     */
    public static void backtrack(int row){
        if(row == N){       //若已经等于N，则说明0~N-1已经赋值完毕，直接打印返回
            Print();
            return;
        }
        for (int i = 0; i < N; i++) {
            postion[row] = i;           //第row行皇后的位置在i处
            if(IsOk(row)){
                backtrack(row+1);
            }else{
                /**
                 * 如果第row行的皇后拜访在i(0-N)处可行，则继续向下深度搜索，否则就直接让这层递归函数出栈
                 * 此层函数出栈也就是当前结点不满足继续搜索的限制条件，即回溯到上一层，继续搜索上一层的下一个i值
                 */
            }
        }
    }

    public static void main(String[] args) {
        backtrack(0);
    }
}

0-1背包的回溯解法

给定n个重量为w1，w2，w3，...，wn，价值为v1，v2，v3，...，vn的物品和容量为C的背包，求这个物品中一个最有价值的子集，使得在满足背包的容量的前提下，包内的总价值最大。

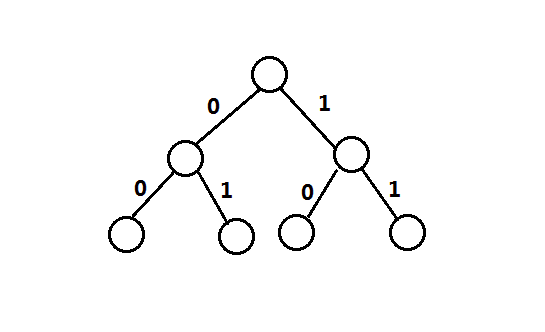
这个问题的解空间树是一棵决策树，每个节点都有两个孩子节点，分别对应了是否将这个物品装入背包的两种情况，0表示不装入，1表示装入，则我们可以画出3件物品的解空间树

package BackTrack;

import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;

public class Package {
    
    //0-1背包问题，回溯解法
    public static final int N = 5;      //物品数量
    static int[] values = {4,5,2,1,3};  //物品的价值
    static int[] weights = {3,5,1,2,2}; //物品的质量
    public static final int C = 8;      //背包的容量
    static int MAX = -1;                //记录最大的价值
    static int[] bag = {0,0,0,0,0};     //物品放置情况，bag[i] = 0表示第i个物品未被装入，等于1则表示已装入
    static List<int[]> list = new LinkedList<int[]>();  //保存最优的结果，可能有多个结果，所以用链表装
    
    public static boolean IsOk(int[] bag, int level) {  //判断当前背包是否超重
        int weight = 0;
        for (int i = 0; i <= level; i++) {  //计算当前背包中所有的物品的总质量
            if(bag[i] == 1) {   //bag[i] == 1表示这个物品已被装入背包
                weight += weights[i];
                if(weight > C)
                    return false;
            }
        }
        return true;
    }
    
    public static void MaxValue(int[] bag, int level) {
        if(level == N) {                //已经判断完最后一个物品
            //先计算当前总价值
            int value = 0;
            for (int i = 0; i < N; i++) {
                if(bag[i] == 1) {
                    value += values[i];
                }圆排列
            }
            if(value > MAX) {
                list.clear();       //发现更优的结果
                MAX = value;
                list.add(bag.clone());
            }else if (value == MAX) {   //其他放置情况的最优解
                list.add(bag.clone());
            }
            return;
        }
        for (int i = 0; i < 2; i++) {
            bag[level] = i;
            if(IsOk(bag, level)) {
                MaxValue(bag, level+1);
            }
        }
    }

    public static void main(String[] args) {
        MaxValue(bag, 0);
        System.out.println(MAX);
        Iterator<int[]> iter = list.iterator();
        while(iter.hasNext()) {
            int[] temp = iter.next();
            for (int i = 0; i < temp.length; i++) {
                System.out.print(temp[i]+" ");
            }
            System.out.println();
        }
    }
}

图的着色问题

  给定无向连通图G=(V, E)和m种不同的颜色，用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中相邻的两个顶点有不同的颜色?
  这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的两个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
  编程计算：给定图G=(V, E)和m种不同的颜色，找出所有不同的着色法。

形如下面这种情况：

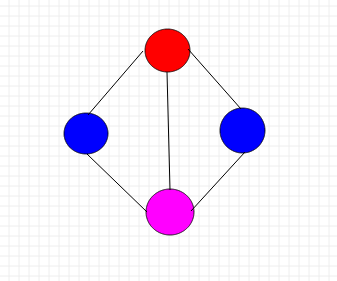
采用回溯策略，对每一个顶点用每一个颜色作尝试，按上图这个例子，3种颜色为这个4个顶点的图着色的解空间树（包括所有可能解和不可能解）有3^4个可能解。即m^n个可能解（m为颜色种数，n为节点个数）。

package BackTrack;

import java.util.Scanner;

public class Paint {

    static int[][] p_Maxtrix = new int[4][4];       //图的邻接矩阵
    static int Colornum = 3;                        //颜色数目
    static int[] result = {-1,-1,-1,-1};            //保存结果
    
    /**
     * @param index         当前顶点的下标
     * @param color         颜色的编号
     * @return                     染色方案是否可行
     */
    public static boolean IsOk(int index, int color) {      //判断是否可以染色
        for (int i = 0; i < p_Maxtrix.length; i++) {
            if(p_Maxtrix[index][i] == 1 && result[i] == color) {
                return false;
            }
        }
        return true;
    }
    
    public static void backtrack(int index) {
        if(index == p_Maxtrix.length) {         //完成最后一个顶点的着色，输出其中一种结果
            for (int i = 0; i < result.length; i++) {
                System.out.print(result[i]+" ");
            }
            System.out.println();
            return;
        }
        for (int i = 0; i < Colornum; i++) {    //对每一种颜色进行尝试
            result[index] = i;
            if(IsOk(index, i)) {
                backtrack(index+1);
            }
            result[index] = -1;
        }
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        for (int i = 0; i <p_Maxtrix.length ; i++) {
            for (int j = 0; j < p_Maxtrix.length; j++) {
                p_Maxtrix[i][j] = in.nextInt();
            }
        }
        backtrack(0);
    }
}

圆排列问题

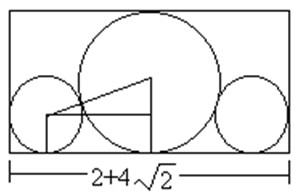
给定n个大小不等的圆c1,c2,…,cn，现要将这n个圆排进一个矩形框中，且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如，当n=3，且所给的3个圆的半径分别为1，1，2时，这3个圆的最小长度的圆排列如图所示。其最小长度为。

算法思路：将每个圆在每个位置上的所有可能作全排列，找出最短距离。

• swap函数：用于交换圆之间的顺序，将两个圆互换位置。

• center函数：计算第t个圆的圆心的坐标，用于给x数组赋值。

• compute函数：其实是在当将最后一个圆排列完成后的操作，计算出当前的排列的距离，与已知的最优解比较，若更优就更新最优解。

• backtrack函数：对每一种排列组合进行回溯尝试。

  参考博文：圆排列

package BackTrack;

public class Round {
    
    public static final int N = 3;          //圆的数目
    static double min = 1000;               //最短距离
    static double[] x = new double[N];      //每个圆的圆心
    static int[] r = {1,1,2};               //每个圆的半径
    static int[] best = new int[N];         //最优解
    
    //交换函数，交换某两个圆的位置
    public static void swap(int[] a, int x, int y) {
        int temp1 = a[x];
        int temp2 = a[y];
        a[x] = temp2;
        a[y] = temp1;位置
    }
    
    /**
     *  对为什么要使用循环做一解释：
     *      因为可能存在第x个圆，它太过于小，而导致其对第x-1和x+1，甚至其他的圆来说，第x个圆存在于不存在都是没影响的
     *      取x-1，和x+1来说：可能x太小，x+1与x-1相切，所以计算第x+1圆心坐标的时候，只能以x-1的圆心与它的圆心来计算
     *      所以要每次循环比较选择最大的那一个做半径
     *      可以参考https://blog.csdn.net/qq_37373250/article/details/81477394中的图
     */
    public static double center(int t) {
        double max = 0.0;               //默认第一个圆的圆心是0.0
        for(int i = 0; i < t; i++) {
            double temp = x[i]+2.0*Math.sqrt(r[i]*r[t]);    //计算得到“以第i个圆的半径和待计算圆的半径”得出的圆心
            //取最大值
            if(temp > max) {
                max = temp;
            }
        }
        return max;
    }
    
    /**
     * 针对为什么不能直接temp = x[N-1]+x[0]+r[N-1]+r[0]（直接用第一个圆到最后一个圆的圆心距离加上两圆半径）做一解释：
     *      为避免第一个圆太小，而第二个圆太大，而导致第二个圆的边界甚至超过了第一个圆的边界，最右边同理
     *      那也可以依次推出可能第三个，第四个...的边界超过了第一个圆的边界，右边同理，所以需要每一个都做一下比较
     *      但是可以放心，x是按圆当前排列顺序放置圆心坐标的
     */
    public static void compute() {          //计算按此排列得到的结果
        double low = 0, high = 0;           //分别表示最左边的边际，和最右边的边际
        for(int i = 0; i < N; i++) {
            if(x[i]-r[i] < low) {
                low = x[i]-r[i];
            }
            if(x[i]+r[i] > high) {
                high = x[i]+r[i];
            }
        }
        double temp = high - low;
        if(temp < min) {
            min = temp;
            for (int i = 0; i < N; i++) {
                best[i] = r[i];
            }
        }
    }
    
    public static void backtrack(int t) {
        if(t == N) {
            compute();
            //return;
        }
        for(int i = t; i < N; i++) {    //t之前的圆已经排好顺序了，可能不是最优解，但是一种可能解
            swap(r, t, i);
            double center_x = center(t);
            x[t] = center_x;
            backtrack(t+1);
            /*下面是使用了较为简陋的剪枝算法进行优化
              if(center_x+r[i] < min) {
                x[t] = center_x;
                backtrack(t+1);
            }             
             */
            swap(r, t, i);          //恢复交换之前的
        }
    }
    public static void main(String[] args) {
        backtrack(0);
        for (int i = 0; i < N; i++) {
            System.out.print(best[i]+" ");
        }
        System.out.println();
        System.out.println(min);

    }
}

连续邮资问题

假设国家发行了n种不同面值的邮票，并且规定每张信封上最多只允许贴m张邮票。连续邮资问题要求对于给定的n和m的值，给出邮票面值的最佳设计，在1张信封上可贴出从邮资1开始，增量为1的最大连续邮资区间。例如，当n=5和m=4时，面值为(1,3,11,15,32)的5种邮票可以贴出邮资的最大连续邮资区间是1到70。

解法思路：解决这个问题其实不光用到回溯，还用到了前面的动态规划策略。

• 首先要明确必须要有一张面值为1的邮票，否则连刚开始一元的邮资都无法贴出。
• 然后就是第x张邮票的面值必须介于第x-1张邮票的面值+1和前x-1张邮票所能贴出的最大邮资+1之间（闭区间）
• 明确前面两点后，回溯的方法就很简单了。每层都是在上一层的面值+1和上一层最大邮资+1之间对所有的可能进行尝试求解最优解。
• 最后就是dp求解每一层的最大邮资问题了。拆解来看，分为向下dp和向右dp，具体dp的理解方法可以参考这篇博文，一些细节问题在下面注释中写出来了。连续邮资问题

package BackTrack;

public class Postage {

    public static final int MAX_Postage = 300;  //最大邮资不应该超过这个值
    public static final int N = 6;                              //所用邮票张数
    public static final int M = 5;                              //所用面值种数        
    public static int[] best = new int[M+1];                    //存放最优解，即所有的面值best[0]不用于存储
    public static int[] x = new int[M+1];                       //当前解
    public static int MAX = 0;                                  //最大邮资
    public static int[][] dp = new int[M+1][MAX_Postage];       //用于动态规划保存第x[0]到x[cur]的最大邮资，dp[i][j] = k表示用i种面值的邮票表示j元最少需要k张
    //应该将dp数组初始化到dp[1][i] = i;      即让第一层都等于张数      
    
    
    public static int findMax(int cur) {        
        if(cur == 1) {          //第一层，只能用面值为1的，能表达出的最大邮资为N（张数）
            return N;
        }
        //向下dp
        int j = 1;      //指示列坐标
        while (dp[cur-1][j] != 0) {
            //此处dp的思路其实就是利用动态规划解决0-1背包问题时的思路，对新加入面值的邮票用与不用？用了用几张的问题？
            //不用时
            dp[cur][j] = dp[cur-1][j];
            //用的时候，用几张？
            for(int i = 1; i*x[cur] <= j; i++) {        //i表示面值张数
                int temp = dp[cur-1][j-i*x[cur]] + i;   //dp[cur-1][j-i*x[cur]]表示除了新加入的面值之外前面所有的面值共同表达j-i*x[cur]元所需张数
                dp[cur][j] = Math.min(temp, dp[cur][j]);        //取最小的张数
            }
            j++;
        }
        
        //向右dp
        while(true) {
            int temp = MAX_Postage;     
            for(int i = 1; i <= cur; i++) {
                /**
                 * 这里很妙，因为向右dp时每次都是向右一个一个推进，所以我们从x[]的第一种面值开始往上加，直到超过限制张数，那么如果x[]的
                 * 第二种面值刚好能将前面的多个第一种替换，那就替换更新张数
                 * 反正意思就是每一次for循环是对前面的较小面值的邮票是一个浓缩的过程
                 */
                temp = Math.min(dp[cur][j-x[i]]+1, temp);
            }
            if(temp > N || temp == MAX_Postage) {     //不管怎么使用当前解x[]中的已知面值，都不能在张数限制内表达出j元
                break;
            }else {
                dp[cur][j] = temp; 
            }
            j++;
        }
        /**对下面这条语句做一个解释
         * 确保同一层上一次dp的结果不会影响下一次**尝试**时的dp，因为可能上一次尝试的一个分支中dp时已经给dp[2][10]赋过值了，但如果没有这一句
         * 就会导致后面的某次尝试时一个分支中dp的时候，向下dp的时候直接将dp[2][10]向下dp了，而事实上，应该向右dp的时候才给dp[2][10]赋值的
         * 其实就是向回溯的下一层发一个信号，表示这块是我上一层dp停止的地方，过了这块可能就是别的回溯分支给dp赋的值了
         */
        dp[cur][j] = 0; 
        return j-1;
    }
    
    public static void backtrack(int t) {                       //t表示当前层数
        if(t == M) {    //已经选够最多的面值种类
            int max = findMax(t);
            if(max > MAX) {
                MAX = max;
                for (int i = 0; i < best.length; i++) {
                    best[i] = x[i];
                }
            }
        //return;   
        }else {
            int temp = findMax(t);                              //得到当前层的最大邮资    
            for(int i = x[t]+1; i <= temp+1; i++) {
                x[t+1] = i;
                backtrack(t+1);
            }           
        }
    }
    
    public static void main(String[] args) {
        for (int i = 0; i <= N; i++) {
            dp[1][i] = i;
        }
        x[0] = 0;
        x[1] = 1;
        backtrack(1);
        System.out.println(MAX);
        for (int i = 0; i < best.length; i++) {
            System.out.print(best[i]+" ");
        }
    }
}