网络流习题集合

其他 2020-03-12 11:16:28 阅读次数: 0

网络流习题

1. 餐巾计划问题

题意: 一共 n n 天，餐厅每天需要 r i r_i 块餐巾。餐厅每天可以花 p p 购买一块新餐巾；或者花 f f 将脏餐巾送到快洗部， m m 天后洗好；或者花 s s 将脏餐巾送到慢洗部， n n 天后洗好，求最小总花费。 ( 1 ≤ n ≤ 2000 , r i ≤ 1 0 7 , p 、 f 、 s ≤ 1 0 4 ) (1\leq n\leq 2000,r_i\leq 10^7,p、f、s\leq 10^4)

思路: 一开始我将每天进行了拆点，然后将右边的点连向左边 i + m i+m 以及 i + n i+n 的点，但建完以后就发现这个模型有问题。该模型的主要问题在于想要达到 ∑ r i \sum r_i 的流量，只能花费 p ∗ ∑ r i p*\sum r_i 的钱，因为源点提供的流量只有花费 p p 一个选择。

因此重新修改思路，需要提供对每一天提供新的流量用于脏布的清洗。因此建图方式如下所示，左边 n n 个点提供每日的脏布，连向右边 i + m i+m 和 i + n i+n 的点。右边的点如果前一天新布用不完，可以传到下一天继续使用。
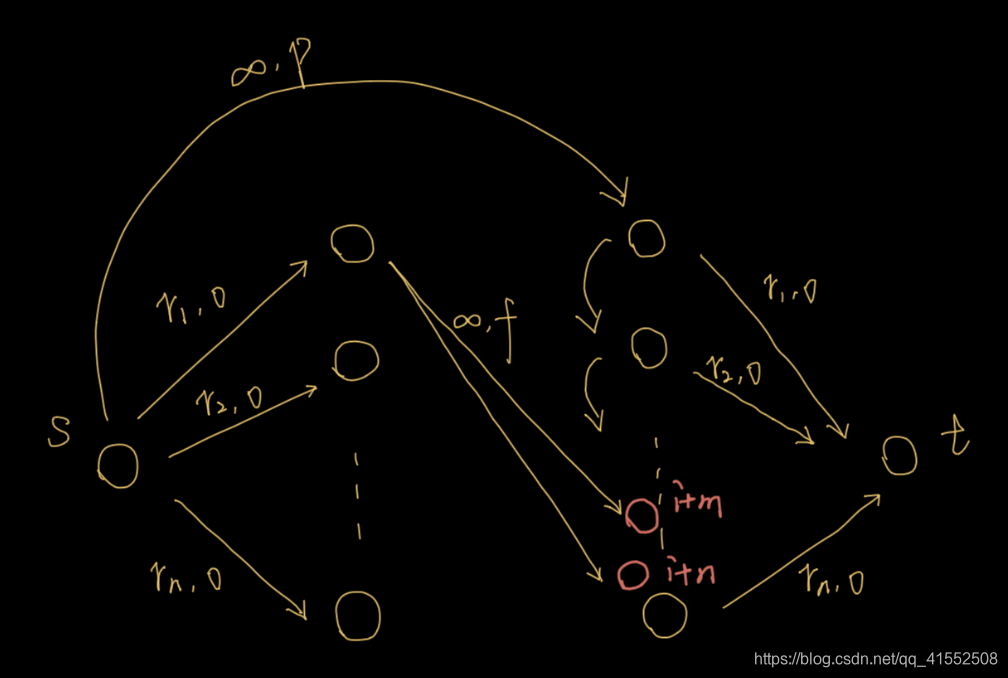
在这里插入图片描述
总结: 此题主要特点就在于分析题干中流量的来源，显然只提供花费 p p 的流量入口是不够的，还需要提供脏布的流量入口。

代码:

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define rep(i,a,b) for(int i = a;i <= b;i++)
typedef long long ll;
const int N = 4100, M = 1e5+100;
const ll inf = 1e15;
using namespace std;

struct Edge{
	int to,next;
	ll cap,cost; //cap为该边的容量，cost为该边的花费
}e[M];
int n,head[N],tot,s,t,vis[N],pre[N]; //tot记录边数，s为源点，t为汇点
ll r[N],dis[N],incf[N]; //dis为到每一个点的最短距离，incf为每一个点流入的流量
//pre为每一个点的最短距离是由哪一条边更新而来，vis标记该点有没有被访问过
ll maxflow,ans,p1,m1,f1,n1,s1;

void init()
{
	tot = 1; //从2开始“成对存储”，2和3是一对，4和5是一对
	memset(head,0,sizeof head);
}

void add(int x,int y,ll z,ll c) //z为容量，c为花费
{
	//正向边，初始容量为z，单位费用为c
	e[++tot].to = y; e[tot].next = head[x]; head[x] = tot; e[tot].cap = z; e[tot].cost = c;
	//反向边，初始容量为0，单位费用为-c，与正向边“成对存储”
	e[++tot].to = x; e[tot].next = head[y]; head[y] = tot; e[tot].cap = 0; e[tot].cost = -c;
}

bool spfa()
{
	//用最短路找增广路
	queue<int> q;
	//建议不要用memset赋值，太容易出错了，当dis设置为long long时
	//tmp还是一个int，就特别容易出错
	fill(dis,dis+N,1e8);
//	memset(dis,0x3f,sizeof dis); //memset是按字节赋值，一个字节8位，一个16进制位表示4个二进制位，因此0x3f为一个字节
	//此处dis赋值为inf，寻找最短路（最小费用流）
	//如果dis赋值为0xcf，则为寻找最长路（最大费用流）
	//0xcf为11001111，因此按位赋值之后为负数
	memset(vis,0,sizeof vis); //每个点都没被访问过
	q.push(s); dis[s] = 0; vis[s] = 1;
	incf[s] = 1<<30; //incf为每一个点流入的流量
	while(q.size())
	{
		int x = q.front(); vis[x] = 0; q.pop();
		for(int i = head[x]; i ; i = e[i].next) //通过与x相连的各边遍历与x相连的点
		{
			if(!e[i].cap) continue; //该边剩余流量为0，不在残量网络中，无法通过
			int y = e[i].to;
			if(dis[y] > dis[x] + e[i].cost)  //如果此处为 < ，则为最长路算法【最大费用流】
			{
				dis[y] = dis[x]+e[i].cost;
				incf[y] = min(incf[x],e[i].cap);
				pre[y] = i; //记录y点的最短路是由哪一条边更新而来的
				if(!vis[y]) vis[y] = 1, q.push(y);
			}
		}
	}
//	int tmp = 0x3f3f3f3f;
	if(dis[t] == 1e8) return false; //汇点不可达，已求出最大流
	return true; 
}

void update()
{
	int x = t;
	while(x!=s)
	{
		int i = pre[x];
		e[i].cap -= incf[t];
		e[i^1].cap += incf[t];
		x = e[i^1].to; //相反边的终点，即为x的上一个点
	}
	maxflow += incf[t];
	ans += dis[t]*incf[t];  //dis[t]为这条最短路上的总花费，incf为这条最短路上的流
}

void solve()
{
	ans = 0; maxflow = 0;
	while(spfa()) update();
	printf("%lld\n",ans);
}

int main()
{
	scanf("%d",&n);
	rep(i,1,n) scanf("%lld",&r[i]);
	scanf("%lld%lld%lld%lld%lld",&p1,&m1,&f1,&n1,&s1);
	//建图过程
	s = 1; t = 2+2*n;
	init();
	add(s,1+n+1,inf,p1);
	rep(i,1,n){
		add(1+n+i,t,r[i],0);
		add(s,1+i,r[i],0);
		if(i != n) add(1+n+i,1+n+i+1,inf,0);
		if(i+m1 <= n) add(1+i,1+n+i+m1,inf,f1);
		if(i+n1 <= n) add(1+i,1+n+i+n1,inf,s1);
	}
	solve();
	return 0;
}
2. [CTSC1999] 家园

题意: 一共 n n 个太空站， m m 个飞船。太空站可以容纳无限人， i i 号飞船只能容纳 H [ i ] H[i] 个人，且每个飞船的飞行路线固定。例如飞船飞行航线为 ( 1 , 3 , 4 ) (1,3,4) ，则具体飞行航线为 134134134... 134134134... 现 0 0 号点为地球， − 1 -1 号点为月球，需要将地球上的 k k 个人转移到月球上，询问最快的转移方案。 ( n ≤ 13 , m ≤ 20 , 1 ≤ k ≤ 50 ) (n\leq 13,m\leq 20,1\leq k\leq 50)

思路: 此题的主要难点应该在于如何在图上体现出这种固定周期的航线。其实这种无限循环的问题在网络流问题中也不是第一次遇见，常见的做法有 ① 枚举答案 + + 建新边 + + 残余网络上继续增广，② 二分答案 + + 新图上跑网络流。而具体的建图方法就是按照时间进行分层。

在此题中，这两种方法都可行，我采用的是第一种枚举答案的方法。即建立一个源点 s s 和汇点 t t ，每一层 n + 1 n+1 个点，不包括月球，因为 t t 就是月球。每一层延展时，第 i i 层的 x x 连向第 i + 1 i+1 层的 x x ，第 j j 个飞船从第 i i 层的第 i i 个位置连向第 i + 1 i+1 层的第 i + 1 i+1 个位置。具体细节可以参考代码中的枚举部分。

总结: 此题主要的收获就是按照时间分层建图的思想，以及不断建新边，然后在残余网络上继续增广求最大流的方法。

代码:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue> 
#define rep(i,a,b) for(int i = a;i <= b;i++)
using namespace std;
const int inf = 1<<29,N = 1000+10,M = 300500;  //处理1e4-1e5规模的网络

struct Edge{ 
	int to,next,v;
}e[M];
int n,m,K,s,t,k;  //顶点个数 边数 源点 汇点 
int head[N],tot,dis[N],mp[N][N];
queue<int> q;
int pos[N],r[N],hp[N]; //当前位置以及循环长度
vector<int> v[N];

void init()   //千万别忘了初始化！
{
	tot = 1; memset(head,0,sizeof head);  //点的编号是2~n，因为2^1 = 3, 3^1 = 2;  符合后续代码的操作 
}

void add(int x,int y,int v)
{
	e[++tot].to = y; e[tot].next = head[x]; e[tot].v = v; head[x] = tot;
	e[++tot].to = x; e[tot].next = head[y]; e[tot].v = 0; head[y] = tot;  //反向边与正向边的流量之和为v 
}

bool bfs()
{
	memset(dis,0,sizeof dis);
	while(!q.empty()) q.pop();
	q.push(s); dis[s] = 1;
	while(!q.empty())
	{
		int x = q.front(); q.pop();
		for(int i = head[x];i;i = e[i].next)
		{
			if(e[i].v && !dis[e[i].to]){
				q.push(e[i].to);


				dis[e[i].to] = dis[x]+1;
				if(e[i].to == t) return 1;  //找到一条路就return 
			}
		}
	}
	return 0;
}

int dinic(int x,int flow) //找增广路 
{
	if(x == t) return flow;
	int rest = flow,k;  //rest为输入的流量 
	for(int i = head[x];i && rest; i = e[i].next)
	{
		if(e[i].v && dis[e[i].to] == dis[x]+1){
			k = dinic(e[i].to,min(rest,e[i].v));
			if(!k) dis[e[i].to] = 0;  //剪枝，去掉增广完毕的点 
			e[i].v -= k;
			e[i^1].v += k;  //反向边加上flow，相当于我们可以反悔从这条路流过 
			rest -= k; //k为能够被送出去的流量 
		}
	}
	return flow-rest;  //总共被送出去了多少流量 
}

int solve()
{
	int flow = 0,maxflow = 0;
	while(bfs())
		while((flow = dinic(s,inf))) maxflow += flow;	
	return maxflow;
}

int fa[N];
inline int find(int x) {return x == fa[x] ? x : (fa[x] = find(fa[x]));}
inline void merge(int x,int y){
	if(x == -1) x = n+1;
	if(y == -1) y = n+1;
	int fx = find(x), fy = find(y);
	if(fx != fy) fa[fx] = fy;
}

int main()
{
	scanf("%d%d%d",&n,&m,&K);
	rep(i,0,n+1) fa[i] = i;
	rep(i,1,m){
		scanf("%d%d",&hp[i],&r[i]);
		rep(j,1,r[i]){
			int xx; scanf("%d",&xx);
			v[i].push_back(xx);
		}
		rep(j,1,r[i]-1) merge(v[i][j],v[i][j-1]);
	}
	int f1 = find(0), f2 =  find(n+1);
	if(f1 != f2) printf("0\n");
	else{
		init();
		s = 1, t = 2;
		add(s,3,K);
		int ans = 0, total = 0;
		while(1){
			total+=solve();
			if(total == K) {printf("%d\n",ans); break;}
			rep(i,1,m){
				int x1 = pos[i], x2 = (pos[i]+1)%r[i];
				int p1 = v[i][x1], p2 = v[i][x2];
				pos[i] = x2;
				if(p1 == -1) continue;
				else p1 = p1+3+ans*(n+1);
				if(p2 == -1) p2 = t;
				else p2 = p2+3+(ans+1)*(n+1);
				add(p1,p2,hp[i]);
			}
			rep(i,0,n){
				int x1 = i+3+ans*(n+1);
				int x2 = i+3+(ans+1)*(n+1);
				add(x1,x2,inf);
			}
			ans++;
		}
	}
	return 0;
}
3. 飞行员配对方案问题

题意: 有 m m 名外籍飞行员， n − m n-m 名英国飞行员，现要将外籍飞行员和英国飞行员两两配对。给出外籍飞行员和英国飞行员的匹配关系，求出最大匹配数，且给出匹配方案。 ( 1 ≤ m ≤ n ≤ 100 ) (1\leq m\leq n\leq 100)

思路: 比较明显的二分图匹配问题，建完图直接跑最大流。最大流算法结束之后再枚举所有边，如果该边连接二分图的两个部分且流量为 0 0 ，则输出其左右端点。

代码:

#include <bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof a);
#define rep(i,a,b) for(int i = a; i <= b; i++)
#define per(i,a,b) for(int i = a; i >= b; i--)
#define __ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
typedef long long ll;
typedef double db;
const db EPS = 1e-9;
const int inf = 1<<29,N = 1000+10,M = 300500;  //处理1e4-1e5规模的网络
using namespace std;

void dbg() {cout << "\n";}
template<typename T, typename... A> void dbg(T a, A... x) {cout << a << ' '; dbg(x...);}
#define logs(x...) {cout << #x << " -> "; dbg(x);}

struct Edge{ 
	int to,next,v;
}e[M];
int n,m,s,t,k;  //顶点个数 边数 源点 汇点 
int head[N],tot,dis[N],mp[N][N];
queue<int> q;

void init()   //千万别忘了初始化！
{
	tot = 1; memset(head,0,sizeof head);  //点的编号是2~n，因为2^1 = 3, 3^1 = 2;  符合后续代码的操作 
}

void add(int x,int y,int v)
{
	e[++tot].to = y; e[tot].next = head[x]; e[tot].v = v; head[x] = tot;
	e[++tot].to = x; e[tot].next = head[y]; e[tot].v = 0; head[y] = tot;  //反向边与正向边的流量之和为v 
}

bool bfs()
{
	memset(dis,0,sizeof dis);
	while(!q.empty()) q.pop();
	q.push(s); dis[s] = 1;
	while(!q.empty())
	{
		int x = q.front(); q.pop();
		for(int i = head[x];i;i = e[i].next)
		{
			if(e[i].v && !dis[e[i].to]){
				q.push(e[i].to);


				dis[e[i].to] = dis[x]+1;
				if(e[i].to == t) return 1;  //找到一条路就return 
			}
		}
	}
	return 0;
}

int dinic(int x,int flow) //找增广路 
{
	if(x == t) return flow;
	int rest = flow,k;  //rest为输入的流量 
	for(int i = head[x];i && rest; i = e[i].next)
	{
		if(e[i].v && dis[e[i].to] == dis[x]+1){
			k = dinic(e[i].to,min(rest,e[i].v));
			if(!k) dis[e[i].to] = 0;  //剪枝，去掉增广完毕的点 
			e[i].v -= k;
			e[i^1].v += k;  //反向边加上flow，相当于我们可以反悔从这条路流过 
			rest -= k; //k为能够被送出去的流量 
		}
	}
	return flow-rest;  //总共被送出去了多少流量 
}

int solve()
{
	int flow = 0,maxflow = 0;
	while(bfs())
		while((flow = dinic(s,inf))) maxflow += flow;	
	return maxflow;
}

int main()
{
	scanf("%d%d",&m,&n);
	init();
	s = n+1; t = n+2;
	while(1){
		int x,y; scanf("%d%d",&x,&y);
		if(x == -1) break;
		add(x,y,1);
	}
	rep(i,1,m) add(s,i,1);
	rep(i,m+1,n) add(i,t,1);
	int ans = solve();
	if(ans == 0) printf("No Solution!\n");
	else{
		printf("%d\n",ans);
		rep(i,2,tot){
			int x = e[i^1].to, y = e[i].to;
			if(1 <= x && x <= m && y >= m+1 && y <= n && e[i].v == 0){
				printf("%d %d\n",x,y);
			}
		}
	}
	return 0;
}
4. 试题库问题

题意: 题库中题目 k k 种类型， n n 为题目总数。现要选出 m m 个题目，要求每种类型至少有 b i b_i 道，每道题目只能充当一种类型。已知每道题目有哪些类型，要求满足条件的一种组卷方案。 ( 2 ≤ k ≤ n ≤ 1000 ) (2\leq k\leq n\leq 1000)

思路: 每道题目只能用一次，属于比较明显的二分图匹配问题，建完图直接跑最大流。最大流算法结束之后再枚举所有边，如果该边连接二分图的两个部分且流量为 0 0 ，则输出其左右端点，和上一题没有较大差别。

代码:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue> 
#define rep(i,a,b) for(int i = a;i <= b;i++)
using namespace std;
const int inf = 1<<29,N = 2000+10,M = 300500;  //处理1e4-1e5规模的网络

struct Edge{ 
	int to,next,v;
}e[M];
int n,m,k,s,t;  //顶点个数 边数 源点 汇点 
int head[N],tot,dis[N],mp[N][N];
queue<int> q;

void init()   //千万别忘了初始化！
{
	tot = 1; memset(head,0,sizeof head);  //点的编号是2~n，因为2^1 = 3, 3^1 = 2;  符合后续代码的操作 
}

void add(int x,int y,int v)
{
	e[++tot].to = y; e[tot].next = head[x]; e[tot].v = v; head[x] = tot;
	e[++tot].to = x; e[tot].next = head[y]; e[tot].v = 0; head[y] = tot;  //反向边与正向边的流量之和为v 
}

bool bfs()
{
	memset(dis,0,sizeof dis);
	while(!q.empty()) q.pop();
	q.push(s); dis[s] = 1;
	while(!q.empty())
	{
		int x = q.front(); q.pop();
		for(int i = head[x];i;i = e[i].next)
		{
			if(e[i].v && !dis[e[i].to]){
				q.push(e[i].to);
				dis[e[i].to] = dis[x]+1;
				if(e[i].to == t) return 1;  //找到一条路就return 
			}
		}
	}
	return 0;
}

int dinic(int x,int flow) //找增广路 
{
	if(x == t) return flow;
	int rest = flow,k;  //rest为输入的流量 
	for(int i = head[x];i && rest; i = e[i].next)
	{
		if(e[i].v && dis[e[i].to] == dis[x]+1){
			k = dinic(e[i].to,min(rest,e[i].v));
			if(!k) dis[e[i].to] = 0;  //剪枝，去掉增广完毕的点 
			e[i].v -= k;
			e[i^1].v += k;  //反向边加上flow，相当于我们可以反悔从这条路流过 
			rest -= k; //k为能够被送出去的流量 
		}
	}
	return flow-rest;  //总共被送出去了多少流量 
}

int solve()
{
	int flow = 0,maxflow = 0;
	while(bfs())
		while((flow = dinic(s,inf))) maxflow += flow;	
	return maxflow;
}

vector<int> ans[N];

int main()
{
	scanf("%d%d",&k,&n);
	init();
	s = n+k+1, t = n+k+2;
	rep(i,1,k){
		int v; scanf("%d",&v);
		add(n+i,t,v);
		m += v;
	}
	rep(i,1,n){
		add(s,i,1);
		int num,pos; scanf("%d",&num);
		rep(j,1,num){
			scanf("%d",&pos);
			add(i,n+pos,1);
		}
	}
	if(solve() == m){
		rep(i,2,tot){
			int x = e[i^1].to, y = e[i].to;
			if(x <= n && y <= n+k && e[i].v == 0) ans[y-n].push_back(x);
		}
		rep(i,1,k){
			printf("%d: ",i);
			for(auto &tv:ans[i]) printf(" %d",tv);
			printf("\n");
		}
	}
	else printf("No Solution\n");
	return 0;
}
5. 太空飞行计划问题

题意: 一共有 m m 个实验， n n 个仪器，每个实验完成之后能得到 p i p_i 的报酬，每个仪器购买需要 v i v_i 的花费，每个实验需要依托某几个对应的器材才能完成。现要求给出购买仪器以及做实验的方案，使得净收益最大，给出具体方案与结果。 ( 1 ≤ n , m ≤ 50 ) (1\leq n,m\leq 50)

思路: 以往普通费用流的问题，其最终的总流量都是固定的，因此可以依据总流量固定这一特点，对流量赋予费用来求解。

而此题的难点恰好在于此，涉及了费用，但最终总流量不固定，如果总流量不固定是很难用费用流算法来建图的，因此我们来考虑最大流。

而最大流通常解决的都是总流量问题，或者有时二分一下答案用最大流来判断是否合法，基本不涉及费用的问题，由此可以判断此题非之前遇到的普通最大流问题，是根据一种特殊的建图方式用最大流来求解出了费用问题。

其实这是一道最大权闭合子图问题，应用最大流最小割定理，通过求解最大流来获得最小割。建图方式如下：

最大权闭合子图问题，针对的是在一个有向图中，每个点都有权值，现要在这个有向图中找到一个闭合子图，即子图中不存在出边不在子图中的点，使该子图中点权值和最大。

具体建图方式则为，有向图中的边流量赋为无穷，源点连向权值为正的点，流量为其权值；权值为负的点连向汇点，流量为其权值绝对值。最终的答案为（正权值之和-最小割）

证明该定理的话，可以通过最小割只能断源点的连边或者汇点的连边来证明，即放弃正权点，或者接纳负权点。最大流结束后，仍与源点相连的点极为最大权闭合子图中的点。

如上建图即可跑出答案，最后的方案输出即 b f s bfs 一遍找到仍与源点相连的点，此处可以依据最大流最后 b f s bfs 的 d i s dis 数组来判断。

总结: 通过此题我们学会了一个用最大流算法解决总流量不固定时的最大收益问题。

代码:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue> 
#define rep(i,a,b) for(int i = a;i <= b;i++)
using namespace std;
const int inf = 1<<29,N = 2000+10,M = 300500;  //处理1e4-1e5规模的网络

struct Edge{ 
	int to,next,v;
}e[M];
int n,m,s,t;  //顶点个数 边数 源点 汇点 
int head[N],tot,dis[N],mp[N][N];
queue<int> q;

void init()   //千万别忘了初始化！
{
	tot = 1; memset(head,0,sizeof head);  //点的编号是2~n，因为2^1 = 3, 3^1 = 2;  符合后续代码的操作 
}

void add(int x,int y,int v)
{
	e[++tot].to = y; e[tot].next = head[x]; e[tot].v = v; head[x] = tot;
	e[++tot].to = x; e[tot].next = head[y]; e[tot].v = 0; head[y] = tot;  //反向边与正向边的流量之和为v 
}

bool bfs()
{
	memset(dis,0,sizeof dis);
	while(!q.empty()) q.pop();
	q.push(s); dis[s] = 1;
	while(!q.empty())
	{
		int x = q.front(); q.pop();
		for(int i = head[x];i;i = e[i].next)
		{
			if(e[i].v && !dis[e[i].to]){
				q.push(e[i].to);
				dis[e[i].to] = dis[x]+1;
				if(e[i].to == t) return 1;  //找到一条路就return 
			}
		}
	}
	return 0;
}

int dinic(int x,int flow) //找增广路 
{
	if(x == t) return flow;
	int rest = flow,k;  //rest为输入的流量 
	for(int i = head[x];i && rest; i = e[i].next)
	{
		if(e[i].v && dis[e[i].to] == dis[x]+1){
			k = dinic(e[i].to,min(rest,e[i].v));
			if(!k) dis[e[i].to] = 0;  //剪枝，去掉增广完毕的点 
			e[i].v -= k;
			e[i^1].v += k;  //反向边加上flow，相当于我们可以反悔从这条路流过 
			rest -= k; //k为能够被送出去的流量 
		}
	}
	return flow-rest;  //总共被送出去了多少流量 
}

int solve()
{
	int flow = 0,maxflow = 0;
	while(bfs())
		while((flow = dinic(s,inf))) maxflow += flow;	
	return maxflow;
}

vector<int> v1,v2;
string S;

int main()
{
	scanf("%d%d",&m,&n); getchar();
	init();
	s = n+m+1, t = n+m+2;
	int ans = 0;
	rep(i,1,m){
		getline(cin,S);
		int len = S.length(), cnt = 0, base = 0;
		rep(j,0,len-1){
			if(S[j] >= '0' && S[j] <= '9'){
				if(base == 0) cnt++;
				base = base*10+S[j]-'0';
			}
			else{
				if(cnt == 1) add(s,i,base), ans += base;
				else add(i,m+base,inf);
				base = 0;
			}
		}
		if(cnt == 1) add(s,i,base);
		else add(i,m+base,inf);
	}
	rep(i,1,n){
		int v; scanf("%d",&v);
		add(m+i,t,v);
	}
	ans -= solve();
	rep(i,1,m+n)
		if(dis[i] != 0){
			if(i <= m) v1.push_back(i);
			else v2.push_back(i-m);
		}
	int sz1 = v1.size(), sz2 = v2.size();
	rep(i,0,sz1-1) printf("%d%c",v1[i]," \n"[i==sz1-1]);
	rep(i,0,sz2-1) printf("%d%c",v2[i]," \n"[i==sz2-1]);
	printf("%d\n",ans);
	return 0;
}
6. 最小路径覆盖问题

题意: 给出一个 n n 个点， m m 条边的 D A G DAG ，现要在该图中找到最少的不相交路径，求出具体路径数。 ( 1 ≤ n ≤ 150 , 1 ≤ m ≤ 6000 ) (1\leq n\leq 150,1\leq m\leq 6000)

思路: 最小路径覆盖问题，如果是第一次遇到该问题，可以先排除费用流的做法，因为总流量不固定，也正因为总流量不固定，我们采取最大流算法。

将一个点拆成两个点，若存在边 ( x , y ) (x,y) ，则将左边的 x x 连向右边的 y y ，最后答案为 a n s = n − m a x f l o w ans = n-maxflow 。接下来给出该算法的大致证明，在构建的图中，若选择了边 ( x , y ) (x,y) ，则意味着在原图中将这两点放在了一条路径中，相当于这两点所在的路径发生了合并，因此总路径数 − 1 -1 ，即最终 a n s = n − m a x f l o w ans=n-maxflow 。

此题还可以扩展到最少相交路径问题（POJ-2594）。而处理最少相交路径只需要将连边条件 ( x , y ) (x,y) 从原图中存在边 ( x , y ) (x,y) 改成原图中 ( x , y ) (x,y) 可达即可，即可以跨越一个点进行路径合并。

代码:

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue> 
#define rep(i,a,b) for(int i = a;i <= b;i++)
using namespace std;
const int inf = 1<<29,N = 2000+10,M = 300500;  //处理1e4-1e5规模的网络

struct Edge{ 
	int to,next,v;
}e[M];
int n,m,s,t;  //顶点个数 边数 源点 汇点 
int head[N],tot,dis[N],mp[N][N];
queue<int> q;

void dbg() {cout << "\n";}
template<typename T, typename... A> void dbg(T a, A... x) {cout << a << ' '; dbg(x...);}
#define logs(x...) {cout << #x << " -> "; dbg(x);}

void init()   //千万别忘了初始化！
{
	tot = 1; memset(head,0,sizeof head);  //点的编号是2~n，因为2^1 = 3, 3^1 = 2;  符合后续代码的操作 
}

void add(int x,int y,int v)
{
	e[++tot].to = y; e[tot].next = head[x]; e[tot].v = v; head[x] = tot;
	e[++tot].to = x; e[tot].next = head[y]; e[tot].v = 0; head[y] = tot;  //反向边与正向边的流量之和为v 
}

bool bfs()
{
	memset(dis,0,sizeof dis);
	while(!q.empty()) q.pop();
	q.push(s); dis[s] = 1;
	while(!q.empty())
	{
		int x = q.front(); q.pop();
		for(int i = head[x];i;i = e[i].next)
		{
			if(e[i].v && !dis[e[i].to]){
				q.push(e[i].to);
				dis[e[i].to] = dis[x]+1;
				if(e[i].to == t) return 1;  //找到一条路就return 
			}
		}
	}
	return 0;
}

int dinic(int x,int flow) //找增广路 
{
	if(x == t) return flow;
	int rest = flow,k;  //rest为输入的流量 
	for(int i = head[x];i && rest; i = e[i].next)
	{
		if(e[i].v && dis[e[i].to] == dis[x]+1){
			k = dinic(e[i].to,min(rest,e[i].v));
			if(!k) dis[e[i].to] = 0;  //剪枝，去掉增广完毕的点 
			e[i].v -= k;
			e[i^1].v += k;  //反向边加上flow，相当于我们可以反悔从这条路流过 
			rest -= k; //k为能够被送出去的流量 
		}
	}
	return flow-rest;  //总共被送出去了多少流量 
}

int solve()
{
	int flow = 0,maxflow = 0;
	while(bfs())
		while((flow = dinic(s,inf))) maxflow += flow;	
	return maxflow;
}

int to[N],deg[N];

int main()
{
	scanf("%d%d",&n,&m);
	init();
	s = 2*n+1, t = 2*n+2;
	int ans = 0;
	rep(i,1,m){
		int x,y; scanf("%d%d",&x,&y);
		add(x,n+y,1);
	}
	rep(i,1,n) add(s,i,1), add(i+n,t,1);
	ans = solve();
	rep(i,2,tot){
		int x = e[i^1].to, y = e[i].to;
		if(x <= n && y <= 2*n && e[i].v == 0){
			to[x] = y-n;
			deg[y-n]++;
		}
	}
	rep(i,1,n){
		if(!deg[i]){
			int pos = i;
			while(pos){
				printf("%d",pos);
				pos = to[pos];
				if(pos == 0) printf("\n");
				else printf(" ");
			}
		}
	}
	printf("%d\n",n-ans);
	return 0;
}
Gene_INNOCENT
发布了244 篇原创文章 · 获赞 115 · 访问量 3万+
私信 关注

猜你喜欢

转载自blog.csdn.net/qq_41552508/article/details/102824509
今日推荐
《美国对全球网络空间安全与发展的威胁和破坏》报告发布
火速冲上 GitHub 热榜 —— 开源编程语言、框架哪有这么可爱？
北京人形机器人创新中心发布全球首个纯电驱拟人奔跑的全尺寸人形机器人“天工”
LFOSSA 源来如此公开课 | 掌握云原生未来：CNCF 认证全面攻略与备考秘籍
国产云输入法——仅华为无云端数据上传安全问题
周排行
Python环境安装与基础语法（1）——计算机基础知识
IMU预积分
ADAS中的LDW、FCW、BSD、LCA、ACC、AEB、APA、DMS代表的含义
B站笔试两道题
skyeye arm 硬件虚拟机环境的搭建
Web前端静态页面示例
数组-合并排序数组 II-简单
springcloud之版本问题启动报错
面向对象-------------匿名对象(六)
输入URL到页面呈现中间发生了什么？
每日归档
更多
2024-04-30(1)
2024-04-29(40)
2024-04-28(0)
2024-04-27(56)
2024-04-26(39)
2024-04-25(22)
2024-04-24(36)
2024-04-23(26)
2024-04-22(39)
2024-04-21(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022