数据结构笔记（一）——基础

1. 算法的特征
   ·输入项(Input)：一个算法有0个或多个输入，对所求解问题特定实例描述的统称；
   ·输出项(Output)：一个算法有一个或多个输出，经计算和处理之后得到的信息，即针对输入问题实例的答案；
   ·确定性(Definiteness)：算法可描述为由若干语义明确的基本操作组成的指令序列；
   ·可行性(Effectiveness)：算法的任每一基本操作在对应的计算模型中均可兑现。
   ·有穷性（Finiteness）：任意算法都应在执行有限次基本操作之后终止并给出输出；
   ·正确性（correctness）：算法所给的输出应该能够符合由问题本身在事先确定的条件。

2. 程序性能分析

·时间复杂度：执行时间的这一变化趋势可表示为输入规模的一个函数，具体地，特定算法处理规模为n的问题所需的时间可记作T（n）。

·渐进复杂度：注重时间复杂度的总体变化趋势和增长速度的策略与方法，即所谓的渐进分析（asymptotic analysis）。
①大O记号：渐进上界（最差时间复杂度）
具体地，若存在正的常数c和函数f（n），使得对任何n>>2都有
$T(n) \leq c \cdot f(n)$
即在n足够大之后，f（n）给出了T（n）增长速度的一个渐进上界，并记为
$T(n) = O(f(n))$
大O记号的性质：
（1）对于任一常数 $c>0$，有 $O(f(n)) = O(c \cdot f(n))$;
（2）对于任意常数 $a>b>0$，有 $O(n^a + n^b) = O(n^a)$。

②大Ω记号：渐进下界（最好时间复杂度）
若存在正的常数c和函数g（n），使得对任何n>>2都有
$T(n) \geq c \cdot g(n)$
即在n足够大之后，g（n）给出了T（n）增长速度的一个渐进下界，并记为
$T(n) = \Omega(g(n))$

③大Θ记号：确界（平均时间复杂度）
若存在正的常数 $c_1 < c_2$和函数h（n），使得对任何n>>2都有
$c_1 \cdot h(n) \leq T(n) \leq c_2 \cdot h(n)$
即在n足够大之后，h（n）给出了T（n）增长速度的一个确界，并记为
$T(n) = \Theta(h(n))$

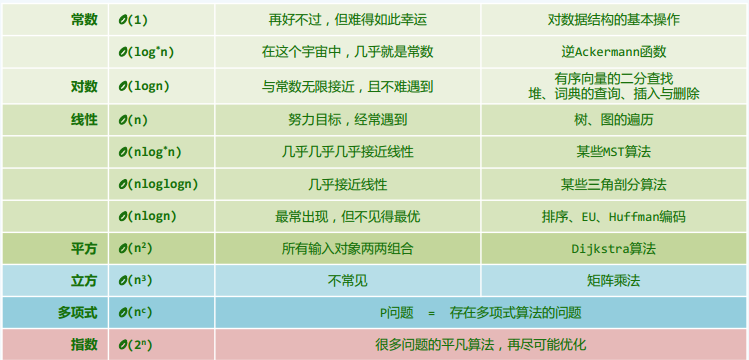
·空间复杂度：程序允许所需内存的大小，可记作S（n）。

3. 减而治之（decrease-and-conquer）算法策略：（线性）递归每深入一层，待求解问题的规模都缩减一个常数，直至最终蜕化为平凡的小（简单）问题。
   ·例：
   $T(n) = T(n-1) + O(1) = T(n-1) + c_1//递推关系$
   $T(0) = O(1) = c_2//边界条件$
   $T(n) = c_1 n + c_2 = O(n)$

4. 分而治之（divide-and-conquer）算法策略：将其分解为若干规模更小的子问题，再通过递归机制分别求解。这种分解持续进行，直到子问题规模缩减至平凡情况。
   ·每一递归实例都可能做多次递归，故称作“多路递归”（multi-way recursion）。通常都是将原问题一分为二，故称作“二分递归”（binary recursion）。但无论是分解为两个还是更大常数个子问题，对算法总体的渐进复杂度并无实质影响。

5. 主定理求时间复杂度：设 $a\geq 1$和 $b > 1$为常数， $f(n)$为一函数， $T(n) = aT(n/b) + f(n)$，则 $T(n)$可能有如下的渐进界：
   ①若 $f(n)<n^{log_b^a}$，且是多项式的小于，即 $\exists \epsilon>0$，有 $f(n) = O(n^{log_b^a - \epsilon})$，则 $T(n) = \Theta(n^{log_b^a})$。
   ②若 $f(n)=n^{log_b^a}$，，则 $T(n) = \Theta(n^{log_b^a}log n)$。
   ③若 $f(n)>n^{log_b^a}$，且是多项式的大于，即 $\exists \epsilon>0$，有 $f(n) = O(n^{log_b^a + \epsilon})$，且对 $\forall c<1$与所有足够大的n，有 $af(n/b) \leq cf(n)$，则 $T(n) = \Theta (f(n))$。