1.线性结构与树形结构的区别

2.二叉树的基本概念和性质
- 二叉树的递归定义:二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的、 互不交的二叉树组成。
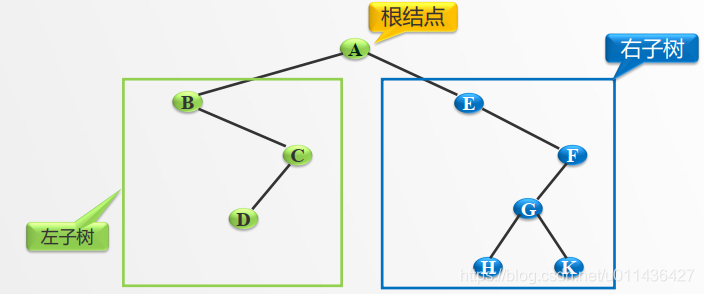
- 二叉树的特点:
⑴ 每个结点最多只有两棵子树,即不存结点度大于2的结点;
⑵ 子树有左右之分,不能颠倒
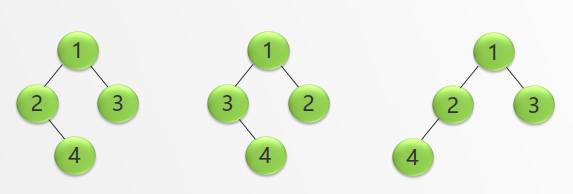
- 二叉树的五种基本形态:
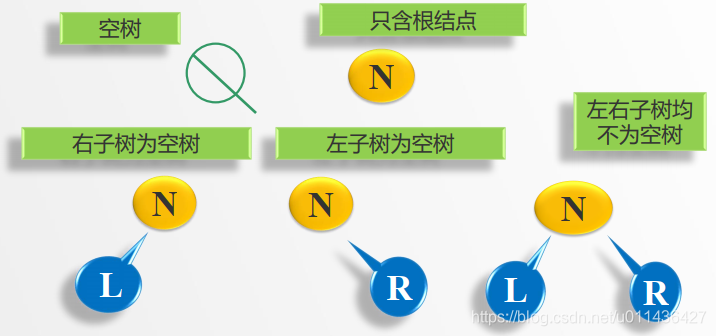
- 基本概念:
(1)节点度:节点所拥有的子树的个数
eg:所有节点的度<=2;
(2)叶子:度为0的节点,eg:D,E
(3)孩子:节点子树的根,eg:节点A子树的根是B
(4)双亲:孩子节点的上层节点,egB和C节点的上层节点是A,所以A是B和C的双亲
(5)子孙:是以某节点为根的子树中的任意一个节点,eg:A有两个子树,任意一个节点都是A的子孙
(6)祖先:从根节点到该节点所经分支上的所有节点,eg:以H节点为例,H沿着这条路径一直到根节点,这条路径上的所有节点都是H节点的祖先
(7)节点的层次:从根节点起,根是第一层,他的孩子是第二层,孩子的孩子是第三层;
(8)兄弟:同一个双亲的孩子节点,eg:B和C
(9)堂兄弟:其双亲在同一层的节点,eg:E和F
(10)二叉树的度:二叉树中最大节点的度数,二叉树的度为2
(11)二叉树的深度:二叉树的最大层次数,eg:G和H层数最大,位于第四层,所以二叉树的深度为4
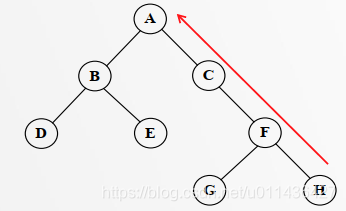
- 两类特殊的二叉树
(1)满二叉树
满二叉树:除了叶子节点,其它节点的度都为2;所有叶子节点都在同一层;
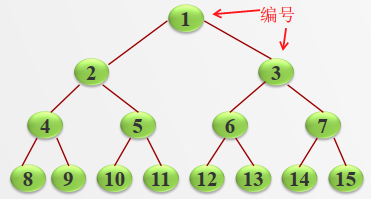
(2)完全二叉树
完全二叉树:节点编号与满二叉树的节点编号是对应的关系
- 二叉树的性质:
(1)性质 1 : 在二叉树的第 i 层上至多有2^(i-1)个结点。 (i≥1)
每层的最大结点个数是确定的。
证明:归纳法证明,i=1时,最多1个节点,第j层,有2^(j-1)个节点,第j+1层,若每个节点有两个孩子,则有:2*2 ^(j-1)个节点,则第j+1层,就有2 ^j个节点,即可证明
(2)性质 2 : 深度为 k 的二叉树上至多含 2^k-1 个结点(k≥1)。
深度一定,二叉树的最大结点数也是确定的。
证明:利用性质1证明,2^0 +21+。。。+2k(一直加到第k层)
(3)叶结点与双分支结点的关系
对任何一棵二叉树T,设叶子结点数为n0,度为2的结点数为n2,那么, n0=n2+1。
证明:n=总的节点个数
n=n0+n1+n2;
由节点分支进行计算,n=2n2+n1+1;
(4)性质4:具有n个结点的完全二叉树的深度为{ |+1
证明:深度为k,最多有 2^k-1 个结点,至少有 2 ^(k-1)-1+1 =2 ^(k-1)个结点;n表示节点数
2^(k-1)<=n<=2 ^k,k-1<= <k,k<= +1,取等号时两边相等

3.完全二叉树的特点
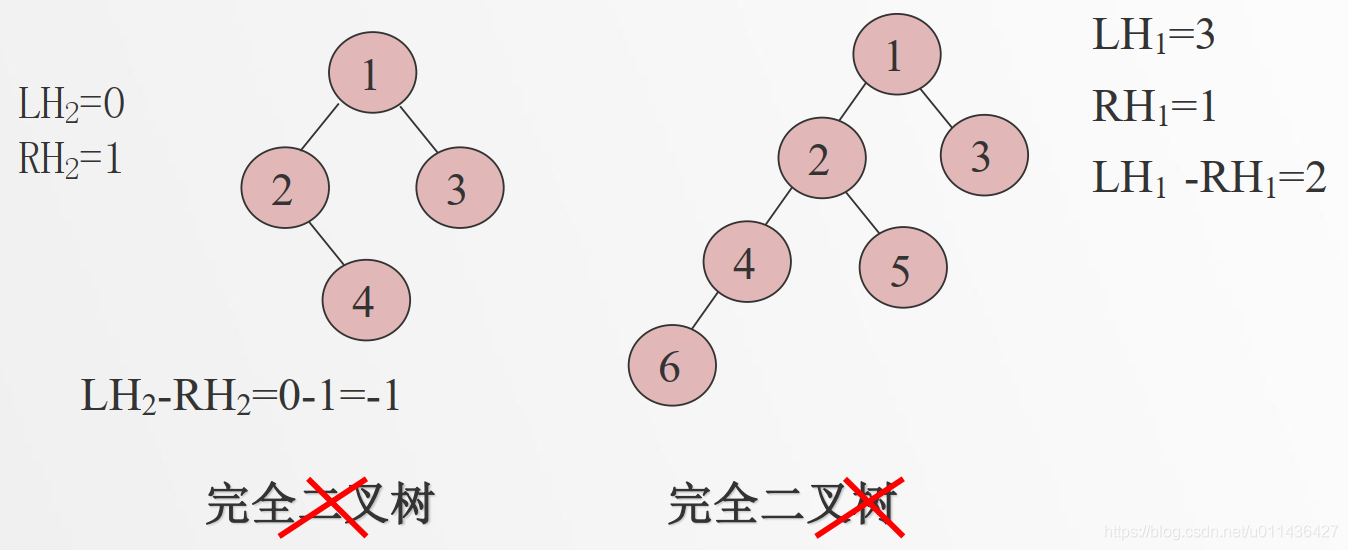
- ( 1) 每个结点i的左子树的深度Lhi-其结点i的右子树的深度Rhi等于0或1, 即叶结点只可能出现在最下层或次最下层。
- (2)完全二叉树结点数n满足2^(k-1)-1<n≤2 ^k-1
- (3)满二叉树一定是完全二叉树,反之不成立。
- 性质5:对有n个结点的完全二叉树的结点按层序编号,则对任一结点i(1<=i<=n), 有:
① 如果i=1, 则结点i是二叉树的根,无双亲;如果i>1, 则其双亲是[i/2](向下取整)
② 如果2i>n, 则结点i无左孩子;如果2i<=n, 则其左孩子是2i
③ 如果2i+1>n, 则结点i无右孩子;如果2i+1<=n, 则其右孩子是2i+1
证明:
假设节点i在第k层,那么他的双亲j是第k-1层的第q个节点(从左往右数),j=2^(k-2)-1+q,i=2 ^(k-1)-1+2(q-1)+1(左孩子的话,偶数),i=2 ^(k-1)-1+2(q-1)+2(右孩子的话,奇数),综上:i=j/2
