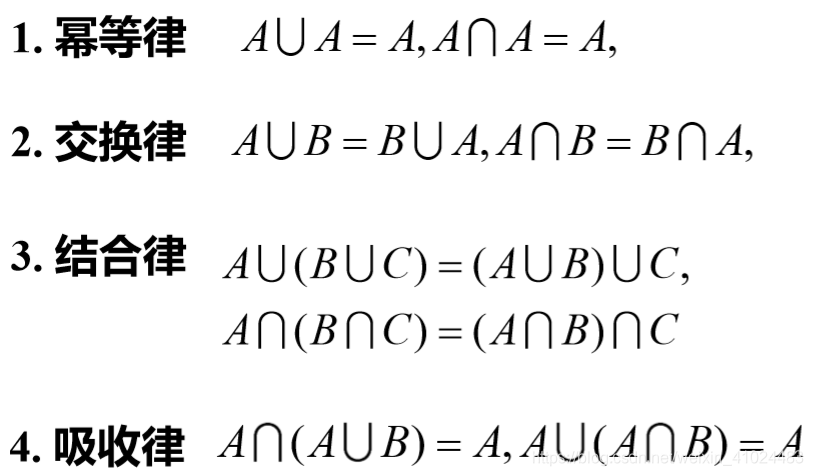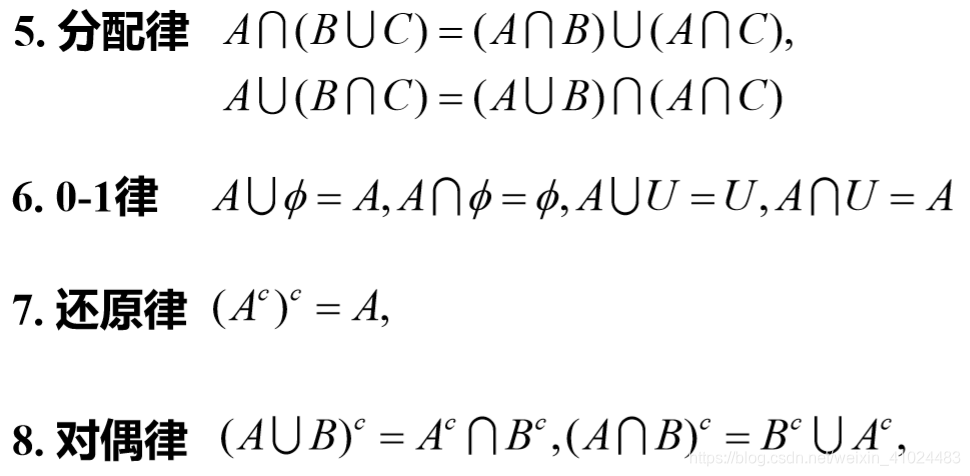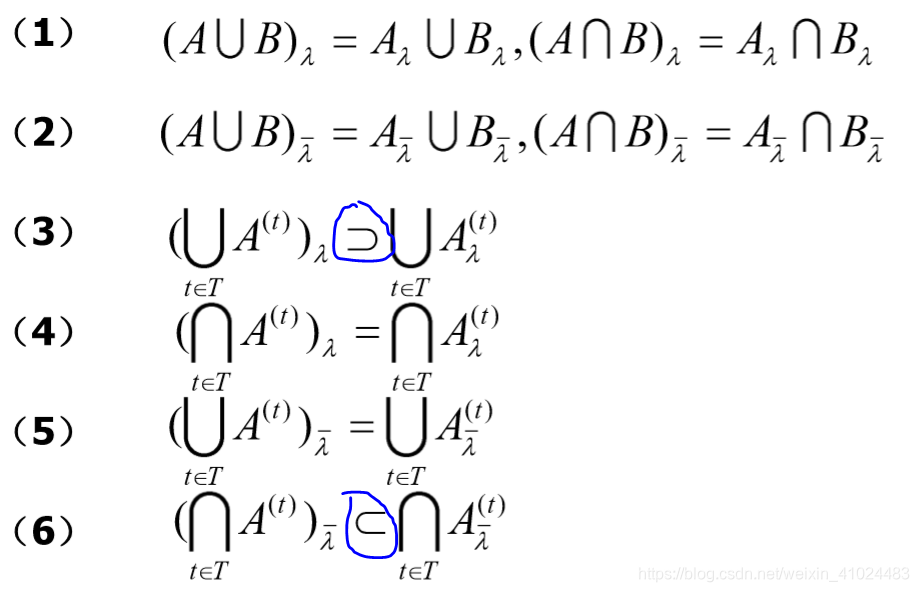模糊数学学习笔记 1：模糊集

个人博客地址 Glooow，欢迎光临~~~

1. 传统集合的定义

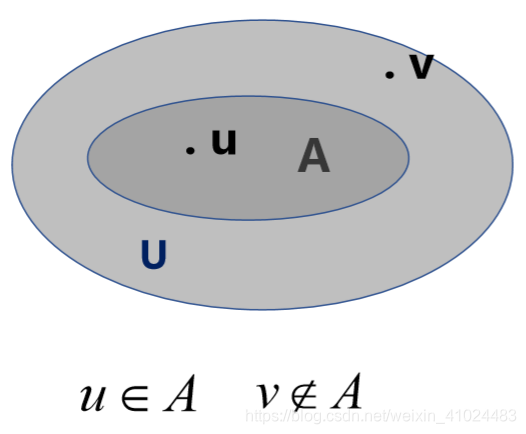
论域 U，集合 A，这可以用一个映射来表示
$\begin{aligned} \chi_{A}: \boldsymbol{U} \rightarrow &\{\mathbf{0}, \mathbf{1}\} \\ \boldsymbol{u} \mapsto & \chi_{A}(\boldsymbol{u}) \end{aligned}$
也可以用一个分段函数来表示
$\chi_{A}(u)=\left\{\begin{array}{ll} {1,} & {u \in A} \\ {0,} & {u \notin A} \end{array}\right.$

2. 模糊集合的定义

模糊集的含义表示其中的元素 $x$ “有一定的可能性”属于集合 $A$，或者说“一定程度上”属于集合 $A$，那么这个属于的程度就被称为隶属度 $\mu_A(x)\in [0,1]$。与传统集合相比，传统集合中元素的隶属程度非 0 即 1，也即要么属于，要么不属于，是确定的，模糊集里则引入了一定的不确定性。也用一个映射表示为
$\begin{aligned} \mu_{A}: &\boldsymbol{U} \rightarrow[0,1] \\ &\boldsymbol{x} \mapsto \mu_{A}(x) \in[0,1] \end{aligned}$
其中映射 $\mu_A$ 称为 $A$ 的隶属函数， $\mu_A(x)$ 为 $x$ 对 $A$ 的隶属度。注意 $\mu_A(x)=0.5$ 时表示最具有模糊性。

3. 模糊集的表示方法

3.1 Zadeh 表示法

$A=\frac{A\left(x_{1}\right)}{x_{1}}+\frac{A\left(x_{2}\right)}{x_{2}}+\cdots+\frac{A\left(x_{n}\right)}{x_{n}}$

这里 $\frac{A\left(x_{i}\right)}{x_{i}}$ 表示 $x_i$ 对模糊集 $A$ 的隶属度为 $A(x_i)$。若论域 $U$ 为无限集，则模糊集表示为
$A=\int_{x\in U} \frac{A(x)}{x}$

3.2 序偶表示法

$A=\left\{\left(x_{1}, A\left(x_{1}\right)\right),\left(x_{2}, A\left(x_{2}\right)\right), \cdots,\left(x_{n}, A\left(x_{n}\right)\right)\right\}$

3.3 向量表示法

$A=(A(x_1),...,A(x_n))$

4. 模糊集的运算

4.1 集合基本运算

• 相等： $A=B \iff A(x)=B(x), \forall x\in U$
• 包含： $A\subset B \iff A(x)\le B(x), \forall x\in U$
• 交集： $(A\cap B)(x) = A(x)\wedge B(x),\forall x\in U$
• 并集： $(A\cup B)(x) = A(x)\vee B(x),\forall x\in U$
• 补集： $A^c(x)=1-A(x),\forall x\in U$

其中记号 $a\wedge b=\min\{a,b\},a\vee b=\max\{a,b\}$

4.2 计算性质

很多计算性质都和普通集合差不多

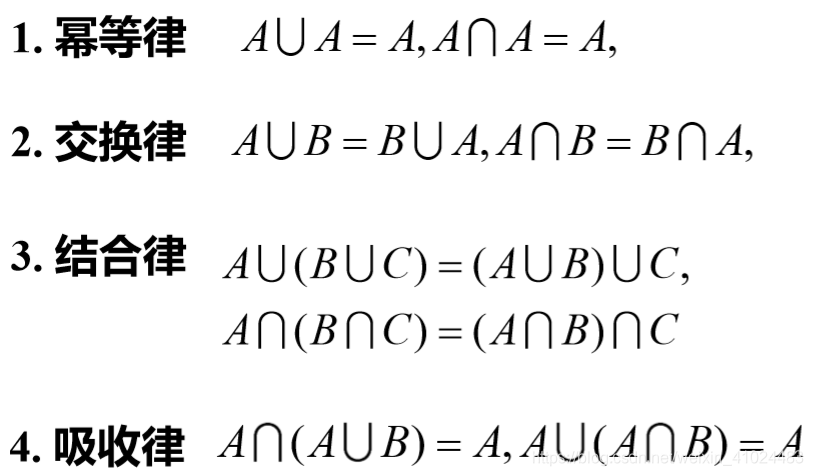
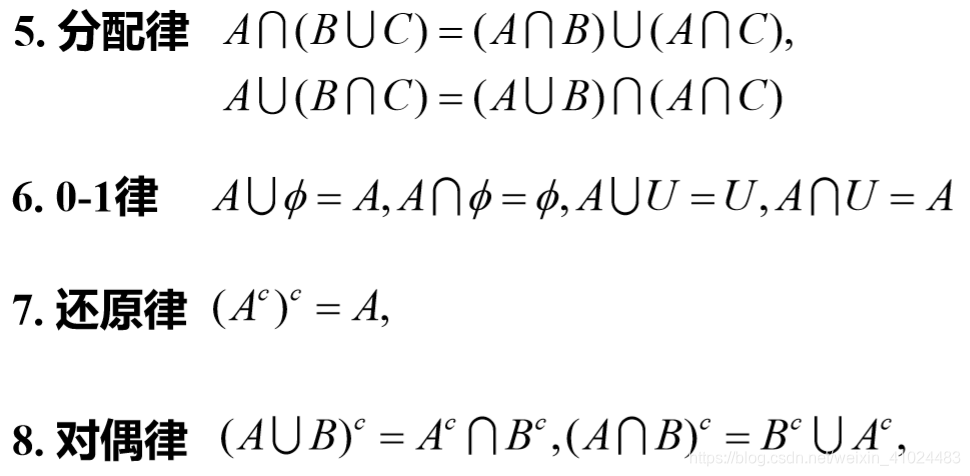
需要注意的是无穷个集合的交集与并集的定义
$\bigcup_{t \in T} A_{t}(a)=\sup_{t \in T} A_{t}(a) \\ \bigcap_{t \in T} A_{t}(a)=\inf_{t \in T} A_{t}(a)$

5. 隶属度的确定

5.1 实验统计法

5.2 (半)解析法

根据问题性质套用现有模糊分布，然后根据测量数据确定分布中的参数。

模糊分布大致分为：偏大型、偏小型、中间型

5.3 专家打分法

根据专家的反馈意见进行统计

6. 截集与分解定理

6.1 截集的定义

定义：若 $A$ 为 $U$ 上的任一模糊集，对 $\forall \lambda\in [0,1]$，记
$A_\lambda = \{x|A(x)\ge\lambda,x\in U\}$
称为 $A$ 的** $\lambda$-截集**，其中 $\lambda$ 称为阈值或置信水平。类似的，**强截集(开截集)**定义为
$A_\lambda = \{x|A(x)>\lambda,x\in U\}$
注意：截集为普通集合，不是模糊集！

6.2 截集运算性质

大部分性质都很简单

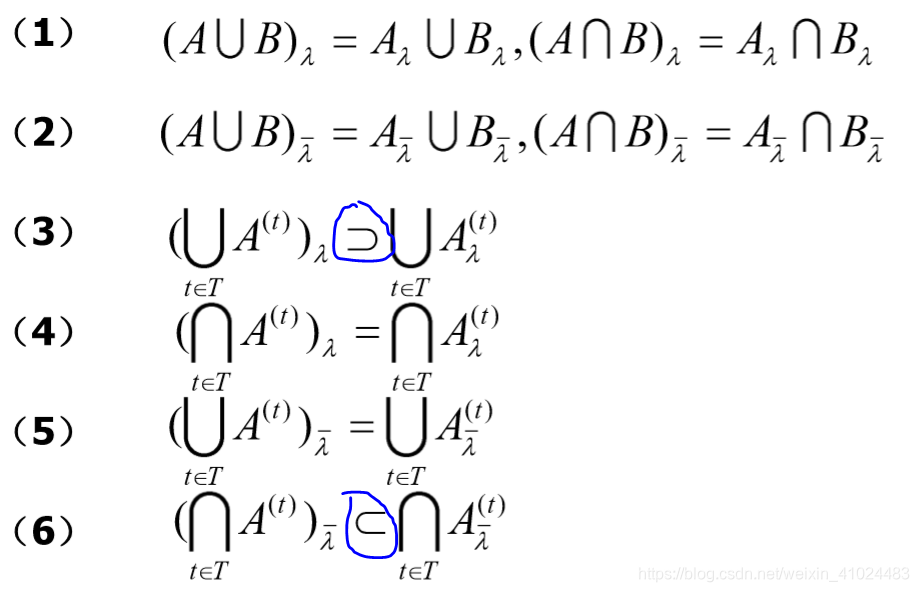
但注意其中第 3 和第 6 条注意并不是相等！！

6.3 一些定义

• 核： $ker(A)=A_1$
• 支集： $supp(A)=A_{\bar{0}}$
• 边界： $A_{\bar{0}}\backslash A_1$
• 数乘： $\lambda A(u) = \lambda \wedge A(u),u\in U$
  • $A\subset B \Rightarrow \lambda A \subset \lambda B$
  • $\lambda_1\le\lambda_2\Rightarrow \lambda_1 A \subset \lambda_2 A$

6.4 分解定理

分解定理 1： $A\in \mathcal{F}(U)$，则 $A=\bigcup_{\lambda\in[0,1]}\lambda A_\lambda$

分解定理 2： $A\in \mathcal{F}(U)$，则