文章目录
极大似然估计(Maximum Likelihood Estimation)
1. 前言
在学习损失函数(loss function)时,思考:对数损失函数(logarithmic loss function)或 对数似然损失函数(loglikelihood loss function)的数学原理时,再次遇到之前一直存在的疑惑——极大似然估计(Maximum Likelihood Estimation)。先总结如下,作为个人学习笔记。本人第一篇笔记,个人拙见,如有不妥与错误,还请指出。
另外发现维基百科中有很好的例子,后续再补上。链接如下:
https://zh.wikipedia.org/wiki/似然函数
2. 通俗理解
例子一
对于抛硬币实验,抛了100次,其中49次正面朝上,51反面朝下,那么我们自然而然得推断,这个硬币是正常的硬币。(如果80次都是正面朝上,我们推断这个硬币有问题。)
硬币的正面朝上次数是真实的实验结果,所以我们“推断”这个硬币是正常的,“硬币是正常的”就是一种模型参数特征,利用实验结论反推模型参数,这就是“似然”(Likelihood)。
例子二
两个黑箱,A箱子有90个白球,10个黑球,B箱子有90个黑球,10个白球,抽出一个白球,那么是从哪个箱子抽出来的。
我们推断白球来自A 箱子,因为A箱子白球更多,更可能抽出白球。抽出白球是实验结果,而推断所抽的那个箱子中球的分布是90个白球,10个黑球即模型参数。这就是似然(Likelihood)。
例子三
一个麻袋里有白球与黑球,但是我不知道它们之间的比例,那我就有放回的抽取10次,结果我发现我抽到了8次黑球2次白球。
要求解最有可能的黑白球之间的比例时,我们就可以采取最大似然估计法:利用8次黑球2次白球这个实验结果,反推最有可能(最大概率)导致这样结果的参数值,这里就是白球黑球的比例。
解:假设抽到黑球的概率为p,即P(抽到黑球)=p,那么得到8次黑球2次白球的这个结果的概率为:

想要得出p是多少很简单,使得P(黑球=8次)最大的p就是我要求的结果。
例子四
假设我们要统计全国人民的年均收入,首先假设这个收入服从服从正态分布,但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的收入。我们国家有10几亿人口呢?那么岂不是没有办法了?
那么这个时候既可以采用极大似然估计法,极大似然就是估计出整个模型的参数。我们比如选取一个城市,或者一个乡镇的人口收入,作为我们的观察样本结果。然后通过最大似然估计来获取上述假设中的正态分布的参数。
有了参数的结果后,我们就可以知道该正态分布的期望和方差了。也就是我们通过了一个小样本的采样,反过来知道了全国人民年收入的一系列重要的数学指标量!那么我们就知道了极大似然估计的核心关键就是对于一些情况,样本太多,无法得出分布的参数值,可以采样小样本后,利用极大似然估计获取假设中分布的参数值。
总结
利用已知的实验结果,反推最大概率导致这个实验结果的模型参数。通过极大似然估计,估计出模型的重要参数,如均值、方差等等,以备后用。
2. 数学角度
2.1 似然VS概率
概率:已知模型参数,推测实验结果。(已知硬币是标准的,那么正面朝上概率为0.5)。
概率函数:P(x|
) ,
为模型参数已知,x为实验结果未知。
似然:已知实验结果,推测模型参数。(已知正面朝上次数基本占比50%,那么推测硬币是标准的)。
似然函数:P(x|
) ,x为实验结果已知,
为模型参数(待估计)未知。
2.2 最大似然估计分类讲解
(一)离散型随机变量

离散型例子
一人射箭,假设只有上帝知道他的命中率,他自己不知道。射击10次,设每次命中概率为p。由于每次射箭都是独立同分布的。
故而,射击10次,他命中4次的概率:

他一共射箭射了3轮,每一轮10次,第一轮命中4次,第二轮命中5次,第三轮命中6次。构造似然函数:

由函数L( P )可知,当p取0.5时,L( P )有最大值,即命中的最大似然估计值。
前面我们已经假设,我们事先并不知道概率为0.5,只有上帝知道,但是我们算出来的结果是与真实的上帝所知道的0.5是相同的。
总结:当P与真实的命中率相近(这里是相等)时,该事件才最有可能发生;反过来,若某事件以最大可能发生了,那么它一定会与真实的实验结果极其相似。
(二)连续型随机变量

连续型例子
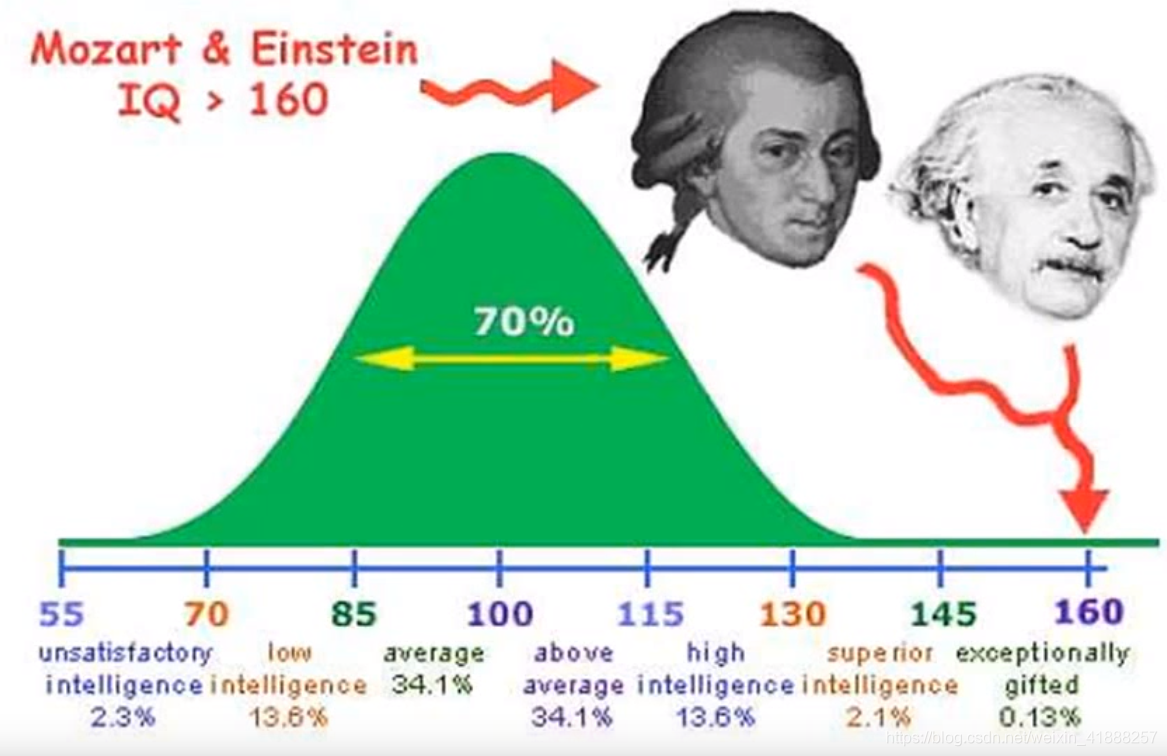
如上图所示,表示的是人群智商的正态分布。服从正态分布:

随机抽取100人,每个人的智商取值为x1,x2,…xn,由于这100人的智商服从独立同分布。似然函数:

要使似然函数取到最大值,此时的 尖 即为对 的最大似然估计,它会和真实的人群智商均值很接近,也就是图中的100左右。当 =100时,(与真实值相同)L( )会取到最大值。
(三)最大似然估计的一般求解步骤

补充说明:
- 之所以第二步需要对L取对数,是因为连乘的函数难以求导,但是取对数以后变成了相加的多项式,便于求导,求极值。
- 若求导无解,则说明 L( P )是单调函数,假设是单调递增的,那么取到 的最大值,也就取到了 L( P )的最大值。
总结
最大似然估计就是:通过真实的实验结果来推测未知的模型的参数,也就是找到一个合理的模型参数,使得实验发生的这个事实存在的概率最该。
参考:
[1]:https://zhuanlan.zhihu.com/p/26614750
[2]: https://blog.csdn.net/shengchaohua163/article/details/78471555
[3]: https://www.bilibili.com/video/av15944258/?spm_id_from=333.788.videocard.0
[4]:https://blog.csdn.net/qq_39355550/article/details/81809467
