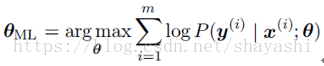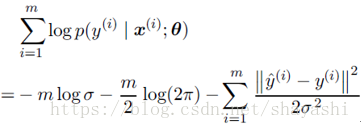极大似然估计是概率论在统计学的应用,是一种参数估计。说的是已知随机样本满足某种具体参数未知的概率分布,参数估计就是通过若干次试验,利用结果推出参数的大概值。极大似然估计的一种直观想法是已知某个事件发生了,我们应该估计使该事件发生的概率最大。例如甲箱有99个白球1个黑球,乙箱有1个白球99个黑球,随机选出一个箱子再从箱子中随机选出一个球是白球,那么我们假设该白球是从甲箱中取出的,因为甲箱取出白球的概率远大于乙箱取出白球的概率。
假设样本集合是 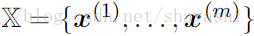
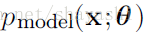
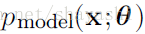
因为乘积的形式不容易计算,所以变换乘积为求和形式:
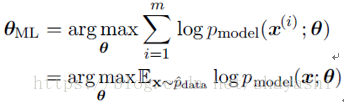
我们知道KL散度的计算公式是:
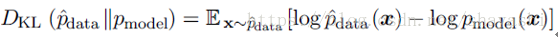
等号右侧第一项是数据生成过程,所以减小KL散度,只需要减小第二项,这与极大似然估计等同。
1. Conditional Log-Likelihood
在监督学习中,我们需要预测的是在给定X的情况下Y的值,所以引出了条件极大似然估计:
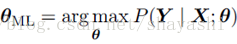
如果样本是i.i.d,等式可以被分解成:
举例:线性回归的极大似然估计
使用均方误差处理线性回归的一般方法是:算法是通过输入x学习输出值 ,使用均方误差来估计 与真实y值之间的距离。
而使用极大似然估计方法的处理是:我们不预测单个的 ,而是生成一个条件分布p(y | x)。现在我们的目标是使分布p(y | x)适合那些所有与x兼容的不同y值。我们定义:
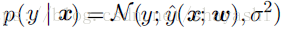
假设样本是i.i.d,条件极大似然估计为:
2. Properties of Maximum Likelihood
极大似然估计最重要的优点是它可以被证明是渐进的最好的估计,随着样本数m的增加,会逐渐收敛。
(图来自deep learning书)