一.什么是图?有哪些特性及其使用场景?
由来: 当我们需要表示多对多的关系的时候,就需要使用到图这种数据结构
定义: 图是一种数据结构,其中顶点可以是具有零个或多个相邻元素.两个顶点之间的连线称为边,节点被称为顶点
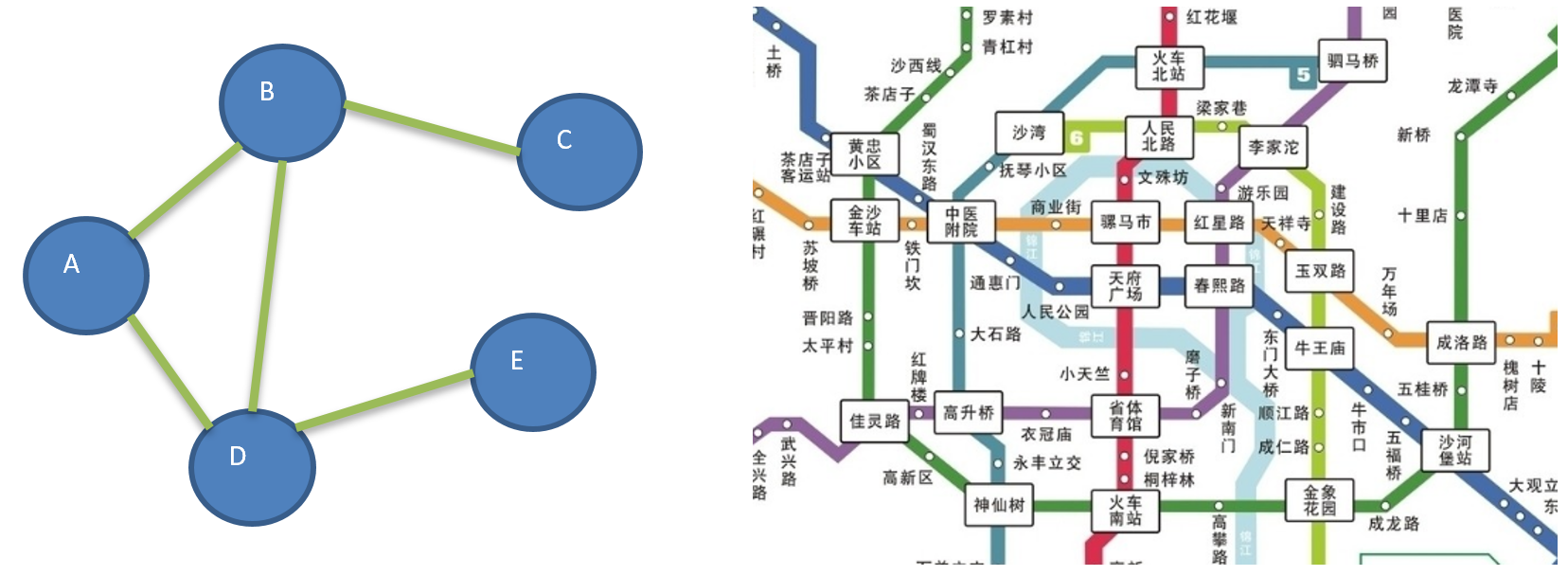
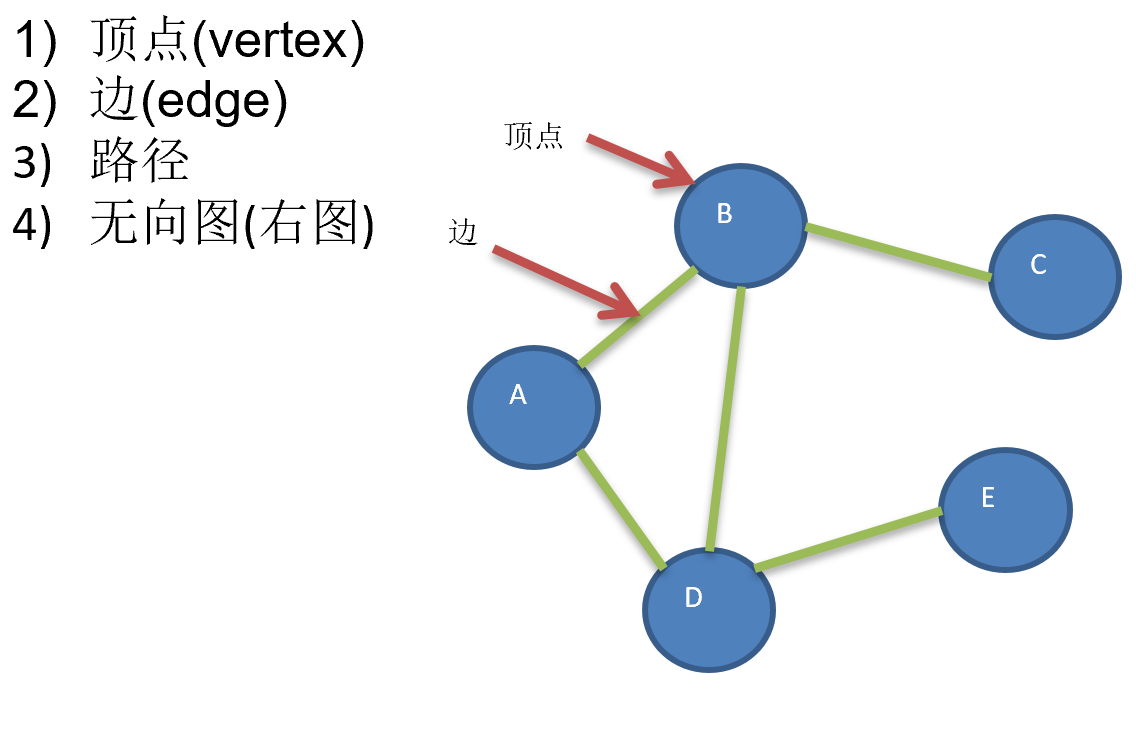
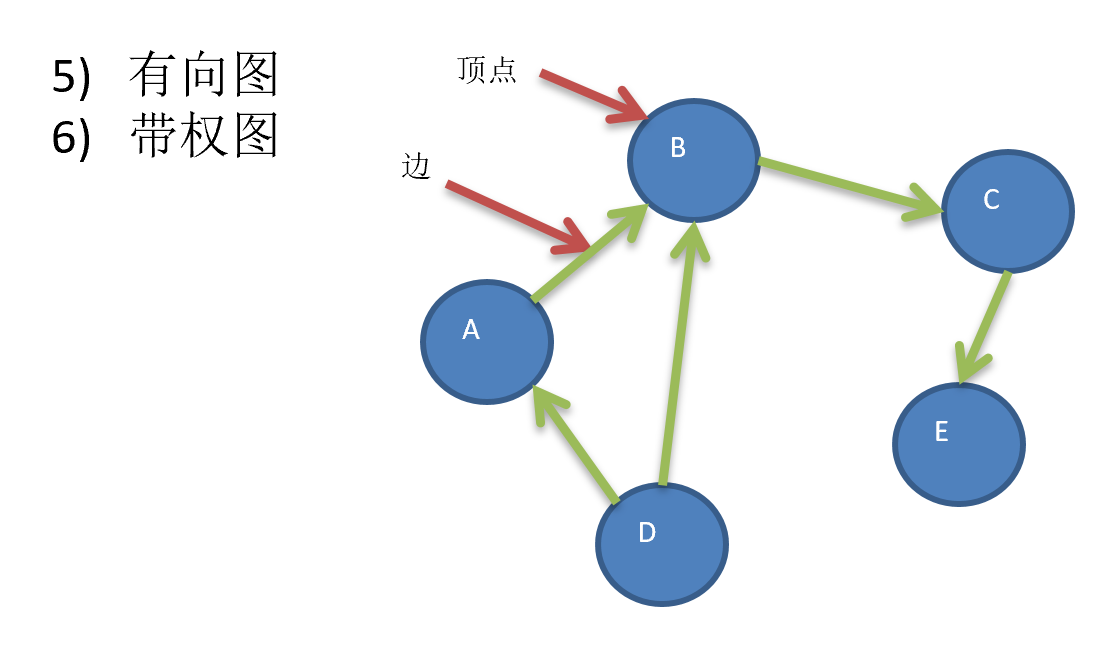
常用概念: 无向图表示顶点之间的连接没有方向,既可以A->B,也可以B->A,有向图表示顶点之间的连接有方向,A->B,B->A,表示不同的路径
图的创建: 邻接矩阵(使用二维数组)和邻接表(使用链表)
public class Graph { private List<String> vertexList; // 存储顶点的集合 private int[][] edges; // 存储图对应的邻接矩阵 private int numberOfEdges; // 表示边的数量 private boolean[] isVisited; // 是否被访问过 public static void main(String[] args) { Graph graph = new Graph(5); String[] vertexes = {"A","B","C","D","E"}; // 添加节点 for (String vertex : vertexes) { graph.insertVertex(vertex); } // 添加边 A-B A-C B-C B-D B-E 用于创建邻接矩阵 graph.insertWeight(0,1,1); graph.insertWeight(0,2,1); graph.insertWeight(1,2,1); graph.insertWeight(1,3,1); graph.insertWeight(1,4,1); graph.showGraph(); } /** * 构造器 ,初始化顶点,邻接矩阵,边的数目,是否访问过 * @param n */ public Graph(int n) { vertexList = new ArrayList<String> (n); edges = new int[n][n]; isVisited = new boolean[n]; numberOfEdges = 0; } }
/** * 插入顶点 * @param vertex */ public void insertVertex(String vertex){ vertexList.add(vertex); } /** * 添加边 无向图 * @param v1 表示第一个顶点对应的下标 * @param v2 表示第二个顶点对应的下标 * @param weight 表示权值 */ public void insertWeight(int v1,int v2,int weight){ edges[v1][v2] = weight; edges[v2][v1] = weight; numberOfEdges++; }
执行结果:

二.图的遍历
深度优先遍历(dfs)
基本思想:
1.从初始访问的节点出发,初始访问的节点可能有多个邻接节点,深度优先遍历的策略是首先访问第一个邻接节点,然后在把这个被访问过的邻接节点
作为初始节点,在访问它的邻接节点.即每次访问完当前节点后首先访问当前节点的第一个邻接节点
2.这样的访问策略是优先纵向的挖掘深入,而不是对所有的节点进行横向的访问
3.这是一个递归调用的过程
步骤:
1.访问初始节点v,并将v标记为已访问
2.查找节点v的第一个邻接节点w
3.若w存在,继续执行4,如果不存在,回到第1步,继续从v的下一个节点继续
4.若w未被访问,对w进行深度优先访问
5.查找节点v的w邻接节点的下一个邻接节点,转到步骤3

/** * 返回节点i对应的数据 * @param i * @return */ public String getValueByIndex(int i){ return vertexList.get(i); } /** * 找到第一个相邻节点的下标 * @param index * @return */ public int getFirstNeighbor(int index){ for (int j = 0; j < vertexList.size(); j++) { if (edges[index][j] != 0){ return j; } } return -1; } /** * 根据前一个相邻节点的下标获取下一个相邻节点的下标 * @param v1 * @param v2 * @return */ public int getNextNeighbor(int v1,int v2){ for (int j = v2+1; j < vertexList.size(); j++) { if (edges[v1][j] != 0) { return j; } } return -1; } /** * 深度优先遍历 * @param isVisited * @param i */ private void dfs(boolean[] isVisited,int i){ // 访问当前的节点 System.out.print(getValueByIndex(i) +"->"); // 将被访问的节点设置成已访问 isVisited[i] = true; // 获取当前节点的相邻的节点 int w = getFirstNeighbor(i); while (w != -1){ // 只要当前节点的邻接点不为空 if (!isVisited[w]){ // 如果没有访问过 dfs(isVisited, w); //继续递归 } // 继续从它的下一个邻接点开始执行 w = getNextNeighbor(i,w); } } public void dfs(){ isVisited = new boolean[vertexList.size()]; for (int i = 0; i < vertexList.size(); i++) { if (!isVisited[i]) { dfs(isVisited, i); } } }
执行结果:

广度优先遍历(bfs)
基本思想:
类似于分层搜索的过程,需要使用一个队列来保存访问过的节点顺序,以便按照这个顺序来访问这些节点的邻接节点
步骤:
1.访问初始节点v,并将v标记为已访问
2.节点v入队列
3.当队列非空时,继续执行,否则算法结束
4.出队列,取出队列头u
5.查找u的第一个邻接节点w
6.若节点u的的邻接节点w不存在,转回步骤3,否则执行步骤7
7.若节点w尚未被访问,则将w标记为已访问
8.节点w入队列
9.查找节点u的继w的邻接节点后的下一个邻接节点,重复步骤6直到队列为空
/** * 广度优先遍历 * @param isVisited * @param i */ private void bfs(boolean[] isVisited, int i){ int u; // 表示队列头结点对应的下标 int w; // 邻接节点w // 用于记录节点访问的顺序 Queue<Integer> queue = new LinkedList<>(); // 访问节点,输出节点的值 System.out.print(getValueByIndex(i) + "->"); // 将已访问的节点标记为已访问 isVisited[i] = true; // 将已访问的节点加入到队列 queue.add(i); while (!queue.isEmpty()){ // 取出队列头节点的下标 u = queue.remove(); // 得到其邻接节点的下标 w = getFirstNeighbor(u); while (w != -1){ // 如果邻接节点存在 if(!isVisited[w]){ // 是否已经访问过该节点 System.out.print(getValueByIndex(w) + "->"); // 访问该节点 isVisited[w] = true; // 将该节点的状态设置为已访问 queue.add(w); // 加入到队列中 } w = getNextNeighbor(u,w); //以u为前驱节点,找到其下一个节点 } } } public void bfs(){ isVisited = new boolean[vertexList.size()]; for (int i = 0; i < vertexList.size(); i++) { if (!isVisited[i]) { bfs(isVisited,i); } } }
执行结果:

三.求解图的最小生成树
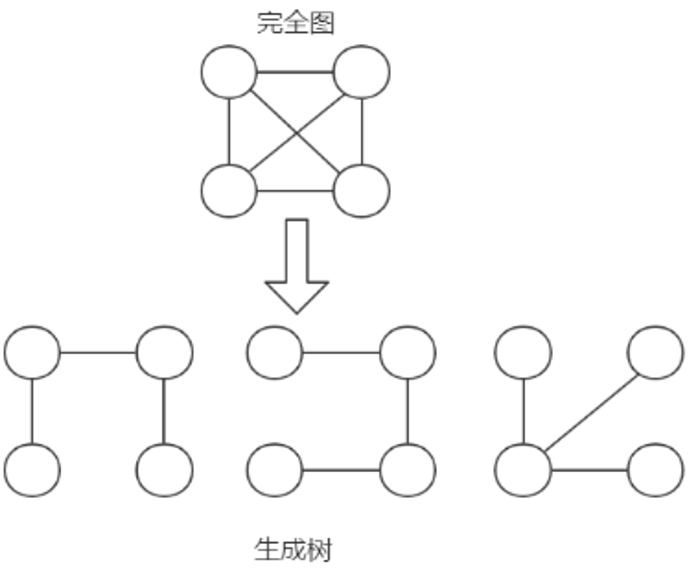
什么是最小生成树?
1.给定一个带权的无向连通图,如何选取一颗生成树,使得树上所有边上权的总和为最小,就叫最小生成树
2.有N个顶点,一定会有N-1条边,并且包含全部的顶点
如何求得最小生成树
1.普里姆算法
步骤:
1.设G=(V,E)是联通网,T=(U,D)是最小生成树,V,U是顶点集合,E,D是边的集合
2.若从顶点u开始构建最小生成树,则从集合V中取出顶点u放入到集合U中,并标记顶点v为已访问
3.若集合U中的顶点ui和集合U-V的顶点vj之间存在边,则寻找这些边权值的最小边,但不能构成回路,将顶点vj加入集合U中,标记顶点v已访问
4.重复步骤2,直到集合V和U相等,并且所有的顶点都标记为已访问,此时D中就有n-1条边
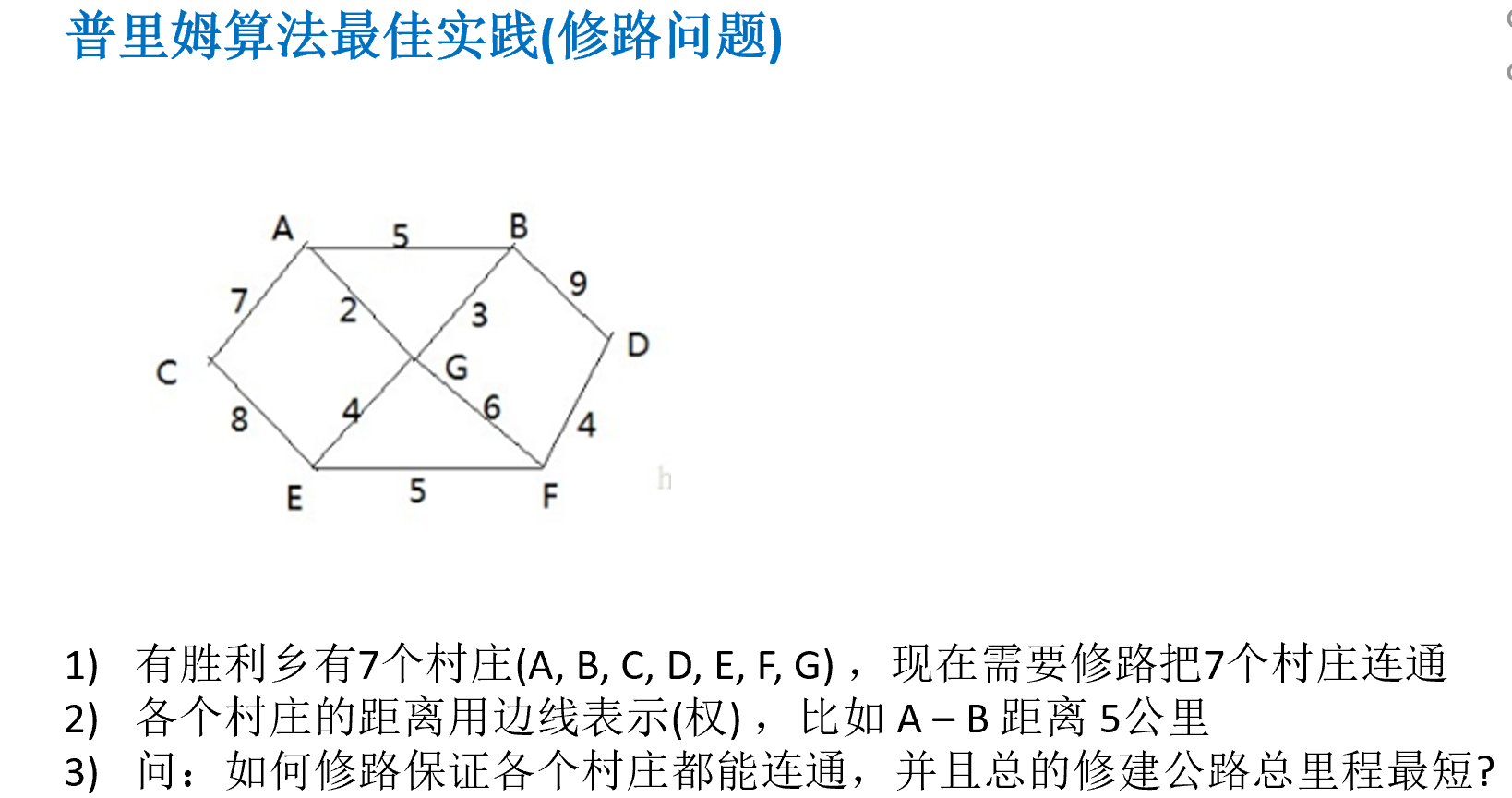
创建图对象并初始化
class MGraph{ int vertexes; // 图的节点个数 char[] data; // 存放顶点坐标 int[][] weight;// 存放边,即邻接矩阵 public MGraph(int vertexes) { this.vertexes = vertexes; data = new char[vertexes]; weight = new int[vertexes][vertexes]; } }
class MinTree { /** * 创建图对象 * @param graph * @param vertexes * @param data * @param weight */ public void createGraph(MGraph graph,int vertexes,char[] data,int[][] weight){ for (int i = 0; i < vertexes; i++) { graph.data[i] = data[i]; for (int j = 0; j < vertexes; j++){ graph.weight[i][j] = weight[i][j]; } } } /** * 显示图的邻接矩阵 * @param graph */ public void show(MGraph graph){ for(int[] link:graph.weight){ System.out.println(Arrays.toString(link)); } } }
public static void main(String[] args) { char[] data = {'A','B','C','D','E','F','G'}; int vertexes = data.length; // 使用10000表示两条线之间不连通 int[][] weight = { {10000,5,7,10000,10000,10000,2}, {5,10000,10000,9,10000,10000,3}, {7,10000,10000,10000,8,10000,10000}, {10000,9,10000,10000,10000,4,10000}, {10000,10000,8,10000,10000,5,4}, {10000,10000,10000,4,5,10000,6}, {2,3,10000,10000,4,6,10000},}; MinTree minTree = new MinTree(); MGraph graph = new MGraph(vertexes); minTree.createGraph(graph,vertexes,data,weight); minTree.show(graph); }
}
执行结果:

实现普利姆算法,假设从G点开始走
/** * 普利姆算法 * @param graph 图对象 * @param v 从哪个顶点开始 */ public void prim(MGraph graph,int v){ // 存放访问过的节点 int[] visited = new int[graph.vertexes]; //初始化visited的值 for (int i = 0; i < graph.vertexes;i++){ visited[i] = 0; } // 把当前的节点标记为已访问 visited[v] = 1; // h1和h2 记录两个顶点的下标 int h1 = -1; int h2 = -1; // 把minWeight设置为一个最大值,表示两个点不能连通,后续会替换 int minWeight = 10000; for (int k = 1; k < graph.vertexes;k++){ // 因为有vertexes个顶点,所以结束后,会生成vertexes-1条边,边的数量 for (int i = 0; i < graph.vertexes;i++){ // i表示已经访问过的节点 for (int j = 0; j < graph.vertexes;j++){// j表示未访问过的节点 if (visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight){ // 寻找已访问的节点和未访问过的节点间的权值最小的边 minWeight = graph.weight[i][j]; // 将minWeight的值更新为图的权重值 h1 = i; // h1更新为已访问 h2 = j; // h2更新为已访问 } } } System.out.println("<" + graph.data[h1] + ", "+graph.data[h2] + "> 权值:"+ minWeight); // 把当前的节点设置为已访问 visited[h2] = 1; // 重置minWeight的值 minWeight = 10000; } }
执行结果:

2.克鲁斯卡尔算法
步骤:
1.按照权值从到到小进行排序
2.保证这些边不构成回路
1.创建图
public class KruskalDemo { private int edgeNums; // 边的数量 private char[] vertexes; // 顶点的集合 private int[][] matrix; // 邻接矩阵 private static final int INF = Integer.MAX_VALUE;// 表示两点之间不能联通 public static void main(String[] args) { char[] vertexes = {'A','B','C','D','E','F','G'}; int matrix[][] = { /*A*//*B*//*C*//*D*//*E*//*F*//*G*/ /*A*/ { 0, 12, INF, INF, INF, 16, 14}, /*B*/ { 12, 0, 10, INF, INF, 7, INF}, /*C*/ { INF, 10, 0, 3, 5, 6, INF}, /*D*/ { INF, INF, 3, 0, 4, INF, INF}, /*E*/ { INF, INF, 5, 4, 0, 2, 8}, /*F*/ { 16, 7, 6, INF, 2, 0, 9}, /*G*/ { 14, INF, INF, INF, 8, 9, 0}}; KruskalDemo kruskal = new KruskalDemo(vertexes,matrix); kruskal.show(); } /*初始化顶点和邻接矩阵*/ public KruskalDemo(char[] vertexes,int[][] matrix){ // 构造方法 int vlen = vertexes.length; //使用复制拷贝的方法初始化顶点 this.vertexes = new char[vlen]; for (int i = 0; i < vertexes.length; i++){ this.vertexes[i] = vertexes[i]; } // 使用复制拷贝的方法,初始化边(权值) this.matrix = new int[vlen][vlen]; for (int i = 0; i < vertexes.length; i++){ for (int j = 0; j < vertexes.length; j++){ this.matrix[i][j] = matrix[i][j]; } } // 初始化有效边的数量 for (int i = 0; i < vertexes.length; i++){ // 自己和自己不算有效边 for (int j = i+1; j < vertexes.length; j++){ if (this.matrix[i][j] != INF){ edgeNums++; } } } } public void show(){ for (int i = 0; i < vertexes.length;i++){ for (int j = 0; j < vertexes.length; j++){ System.out.printf("%d\t",matrix[i][j]); } System.out.println(); } } }
执行结果:

创建边,根据权值进行升序排列
class Edata implements Comparable<Edata>{ public char start; // 边的起始点 public char end; // 边的终点 public int weight; // 边的权值 public Edata(char start, char end, int weight) { this.start = start; this.end = end; this.weight = weight; } @Override public String toString() { return "Edata [<" + start +","+end+">= "+weight+"]"; } @Override public int compareTo(Edata o) { // 升序排列 return this.weight - o.weight; } }
判断两条边是否是同一个终点,如果不是就加入到树中,直到树扩大成一个森林
/** * 返回一个顶点对应的下标值,找不到返回-1 * @param ch * @return */ private int getPosition(char ch){ for (int i = 0; i < vertexes.length;i++){ if (vertexes[i] == ch ){ return i; } } return - 1; } /** * 获取图中的边,放入到Edata数组中, * @return */ private Edata[] getEdges(){ int index = 0; Edata[] edges = new Edata[edgeNums]; for (int i = 0; i < vertexes.length;i++){ for (int j = i+1; j < vertexes.length; j++) { if (matrix[i][j] != INF){ edges[index++] = new Edata(vertexes[i],vertexes[j],matrix[i][j]); } } } return edges; } /** * 获取下标为i顶点对应的终点,用于判断两个顶点的终点是否相同 * @param ends 记录了各个顶点对应的终点是哪个,在遍历过程中,逐步形成 * @param i 传入的顶点对应的下标 * @return 返回这个顶点的终点对应的下标 */ private int getEnd(int[] ends,int i){ while (ends[i] != 0){ i = ends[i]; } return i; }
完成算法
public void kruskal(){ int index = 0; // 表示最后结果的数组索引 int[] ends = new int[edgeNums]; // 用于保存已有最小生成树中每个顶点的终点 Edata[] rets = new Edata[edgeNums]; // 创建结果数组,保留最后的最小生成树 Edata[] edges = getEdges(); // 获取所有边的集合 Collections.sort(Arrays.asList(edges)); // 排序 // System.out.println("图的边的集合=" + Arrays.toString(edges) + " 共"+ edges.length); // 将边添加到最小生成树中,同时判断是否生成回路 for (int i = 0; i < edgeNums; i++){ // 获取第i条边的第一个顶点 int p1 = getPosition(edges[i].start); // 获取第i条边的第二个顶点 int p2 = getPosition(edges[i].end); // 获取p1这个顶点在已有最小生成树中的终点 int m = getEnd(ends,p1); // 获取p2这个顶点在已有最小生成树中的终点 int n = getEnd(ends,p2); // 是否构成回路 if (m != n){ // 如果没有构成回路 ends[m] = n; // 设置m在已有最小生成树中的终点 rets[index++] = edges[i]; // 将这条边加入到结果数组 } } System.out.println("最小生成树为:"); for (int i = 0; i < index; i++){ System.out.println(rets[i]); } }
执行结果:

四.求出图的最短路径
1.迪杰斯特拉算法(从单一顶点出发到其他的各个顶点的最小路径)

步骤:
1.设出发顶点为v,顶点集合V{v1,v2,...vi},v到V中各顶点集合的距离集合Dis,Dis{d1,d2,...di},Dis记录了v到图中各个顶点的距离(到自身可以看做是0,v到vi对应的距离是di)
2.从Dis中选择值最小的di并移出Dis集合,同时移除V集合对应的顶点vi,此时的v到vi即为最短路径
3.更新Dis集合,比较v到V集合中顶点的距离值,与v通过vi到V集合中顶点的距离值,保留较小的那个(同时也应该更新顶点的前驱节点为vi,表示通过vi达到的)
4.重复步骤2和3,直到最短路径顶点为目标顶点即可结束
初始化图
public static void main(String[] args) { char[] vertexes = {'A','B','C','D','E','F','G'}; int[][] matrix = new int[vertexes.length][vertexes.length]; final int N = 65535;// 表示不可以连接 matrix[0]=new int[]{N,5,7,N,N,N,2}; matrix[1]=new int[]{5,N,N,9,N,N,3}; matrix[2]=new int[]{7,N,N,N,8,N,N}; matrix[3]=new int[]{N,9,N,N,N,4,N}; matrix[4]=new int[]{N,N,8,N,N,5,4}; matrix[5]=new int[]{N,N,N,4,5,N,6}; matrix[6]=new int[]{2,3,N,N,4,6,N}; Graph g = new Graph(vertexes,matrix); g.showGraph(); } class Graph { public char[] vertexes; public int[][] matrix; public VisitedVertex vv; public Graph(char[] vertexes, int[][] matrix) { this.vertexes = vertexes; this.matrix = matrix; } public void showGraph(){ for (int[] links:matrix){ System.out.println(Arrays.toString(links)); } } }
执行结果:

初始化前驱节点,已访问节点和距离
class VisitedVertex { /*记录各个顶点是否访问过,1表示已访问,0表示未访问*/ public int[] already_arr; /*记录每一个下标对应值的前一个下标,动态更新*/ public int[] pre_visited; /*记录出发顶点到各个顶点的距离*/ public int[] dis; /** * * @param length 初始化顶点的个数 * @param index 从哪个顶点开始 */ public VisitedVertex(int length,int index) { already_arr = new int[length]; pre_visited = new int[length]; dis = new int[length]; /*初始化dis数组*/ Arrays.fill(dis,65535); /*设置除法顶点被访问过*/ this.already_arr[index] = 1; /*设置出发顶点的访问距离为0*/ this.dis[index] = 0; } /** * 判断某各顶点是否被访问过 * @param index * @return */ public boolean in(int index){ return already_arr[index] == 1; } /** * 更新出发顶点到index节点的距离 * @param index * @param len */ public void updateDis(int index,int len){ dis[index] = len; } /** * 更新pre这个顶点的前驱节点为index顶点 * @param pre * @param index */ public void updatePre(int pre,int index){ pre_visited[pre] = index; } /** * 返回出发顶点到index的距离 * @param index * @return */ public int getDis(int index){ return dis[index]; } /** * 继续选择并返回新的访问节点 * @return */ public int updateArr(){ int min = 65535; int index = 0; for (int i = 0; i < already_arr.length;i++){ if (already_arr[i] == 0 && dis[i] < min){ //使用广度优先的策略,如果初始节点的下一个没有被访问,并且可以连通,就选择下一个节点为出发节点 min = dis[i]; index = i; } } /*更新index顶点被访问过*/ already_arr[index] = 1; return index; } }
更新周围顶点和前驱节点的距离,完成算法
public void djs(int index){ vv = new VisitedVertex(vertexes.length,index); /*更新index顶点到周围顶点的距离和前驱节点*/ update(index); for (int j = 1; j < vertexes.length; j++) { /*选择并返回新的访问节点*/ index = vv.updateArr(); /*更新index顶点到周围顶点的距离和前驱节点*/ update(index); } } /** * 更新index下标顶点周围顶点的距离和周围顶点的前驱节点 * @param index */ public void update(int index){ int len = 0; /*遍历邻接矩阵的matrix[index]所对应的行*/ for (int i = 0; i < matrix[index].length; i++) { /*出发顶点到index顶点的距离 + 从index到i顶点的距离和*/ len = vv.getDis(index) + matrix[index][i]; /*如果i顶点没有被访问过,并且len小于出发顶点到j顶点的距离,就需要更新*/ if (!vv.in(i) && len < vv.getDis(i)){ /*更新i点的前驱节点为index节点*/ vv.updatePre(i,index); /*更新出发顶点到i的距离*/ vv.updateDis(i,len); } } }
执行结果:

2.弗洛伊德算法(求出所有顶点到其他各个顶点的最短距离)
步骤:
1.设顶点vi到vk的最短路径已知是Lik,顶点vk到vj的最短路径已知是Lkj,顶点vi到vj的路径为Lij,那么vi到vj的最短路径是min((Lik+Lkj),Lij),vk的取值为图中所有的顶点
则可以获得vi到vj的最短路径
2.vi到vk的最短路径Lik,vj到vk的最短路径Lkj,可以用同样的方式获得(递归)
初始化图
public static void main(String[] args) { char[] vertexes = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' }; //创建邻接矩阵 int[][] matrix = new int[vertexes.length][vertexes.length]; final int N = 65535; matrix[0] = new int[] { 0, 5, 7, N, N, N, 2 }; matrix[1] = new int[] { 5, 0, N, 9, N, N, 3 }; matrix[2] = new int[] { 7, N, 0, N, 8, N, N }; matrix[3] = new int[] { N, 9, N, 0, N, 4, N }; matrix[4] = new int[] { N, N, 8, N, 0, 5, 4 }; matrix[5] = new int[] { N, N, N, 4, 5, 0, 6 }; matrix[6] = new int[] { 2, 3, N, N, 4, 6, 0 }; FGraph fGraph = new FGraph(vertexes,matrix,vertexes.length); fGraph.show(); } class FGraph{ public char[] vertexes; // 存放各个顶点的数组 public int[][] dis; // 存放各个顶点到其他各顶点的距离 public int[][] pre; // 存放到达目标顶点的前驱节点 /** * 初始化顶点,dis,pre * @param vertexes * @param matrix * @param length */ public FGraph(char[] vertexes, int[][] matrix, int length) { this.vertexes = vertexes; this.dis = matrix; /*对pre数组进行初始化,存放的是前驱节点的下标*/ this.pre = new int[length][length]; for (int i = 0; i < length; i++) { Arrays.fill(pre[i], i); } } public void show() { for(int k = 0; k < dis.length;k++){ // 输出pre for (int j = 0; j < dis.length; j++) { System.out.print(vertexes[pre[k][j]] + " "); } System.out.println(); // 输出dis for (int i = 0; i < dis.length; i++) { System.out.print("(" + vertexes[k] + "到"+vertexes[i]+"的最短路径是: " + dis[k][i] + ") "); } System.out.println(); } } }
实现算法(vki+vkj < vij)
public void floyd(){ int len = 0; // 保存距离 /*对中间节点进行遍历,k就是中间节点的下标 [A, B, C, D, E, F, G] */ for (int k = 0; k < dis.length; k++) { /*从i顶点开始出发 [A, B, C, D, E, F, G] */ for (int i = 0; i < dis.length; i++) { /*到达j顶点 [A, B, C, D, E, F, G] */ for (int j = 0; j < dis.length; j++) { /*计算出从i出发,经过k中间节点,到达j的距离*/ len = dis[i][k] + dis[k][j]; if (len < dis[i][j]) {/*如果len小于原本的距离*/ /*更新距离表*/ dis[i][j] = len; /*更新前驱节点*/ pre[i][j] = pre[k][j]; } } } } }
执行结果:
