台湾国立大学郭彦甫Matlab教程笔记（22） Cramer's method(Inverse matrix逆矩阵法)

台湾国立大学郭彦甫Matlab教程笔记（22） Cramer’s method(Inverse matrix)

matrix left division左除:\ or mldivide()

solving systems of linear equations Ax=b using factorization methods:

求Ax=b中的x，只需要A\b
实际上，A\b这个算式matlab进行了很多判断，进行了很多演算，时间复杂度有点高
左除本质上也是succesive elemination 逐次消去法
看一个线性方程组
在这里插入图片描述
matlab指令：
A=[1,2,1;2,6,1;1,1,4];
b=[2;7;3];
x=A\b

执行的结果：算出来x的值：
在这里插入图片描述

一道练习题：需要结合上一次笔记
在这里插入图片描述
关键点在于用matlab中矩阵把线性方程表述出来，然后求解，应该不难。
笔者的练习如下：

思考：这里需要用符号法syms吗？
在这里插入图片描述我的练习：

syms R1 R2 R3 R4 R5 V1 V2
A=[R1 0 0 R4 0; 0 R2 0 -R4 R5; 0 0 -R3 0 R5; 1 -1 0 -1 0; 0 1 -1 0 -1]
b=[V1;0;V2;0;0]

执行一下，发现可以：
在这里插入图片描述

接下来就是求解的问题了，我想到的是用左除\

x=A\b

运行结果，这个用符号表示的线性方程组解出来了。

在这里插入图片描述
下面讲一些矩阵分解的一些函数

Matrix decomposition funcitons矩阵分解函数

qr(): orthogonal-triangular decomposition 正交三角矩阵的分解
ldl(): Block LDL’s factorization for Hermitian indefinite matrices(厄密特不定矩阵)
ilu():Sparse稀疏 incomplete LU factorization 稀疏矩阵的LU不完全分解
lu();LU matrix factorization LU分解
chol(): Cholesky factorization Cholesky 针对的是正定矩阵的分解，也称平方根法
gsvd(): generalized singular value decomposition 广义奇异值分解
svd():singular value decomposition奇异值分解

下面来到 cramer’s method

Cramer’s(Inverse) method

在这里插入图片描述
A的逆矩阵： A^-1:inverse of A

可以求出x矩阵

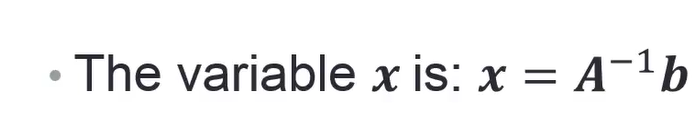
Inverse Matrix逆矩阵

对于矩阵A，A的逆矩阵被定义为：
det（A）是矩阵A的行列式，是determinant的缩写
adj(A)是A矩阵的伴随矩阵(对整个矩阵求代数余子式，这些代数余子式构成的新的矩阵) 在这里是A中的a 和d 交换，b和c之间加负号
在这里插入图片描述
性质：
A的逆矩阵再取逆，还是A；
kA的逆矩阵等于1/k乘以A的inverse

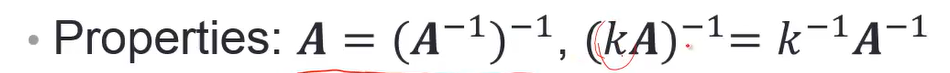
在这里插入图片描述

接下来讲解如何用cramer’s method 求解方程组

solving equations using Cramer’s Method

下面的方程组例子

在这里插入图片描述
我们要求解x

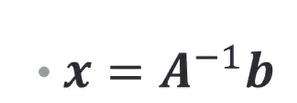
在matlab中

A=[1,2,1;2,6,1;1,1,4];
b=[2;7;3];
x=inv(A)*b

可以得到这个方程组的解

在这里插入图片描述
Cramer’s method 有一个问题：A的逆矩阵不一定存在
三元一次方程组，是三个平面之间的关系
可能有唯一解，可能无限解，可能无解
举例：矩阵中的两行成比例，A的逆矩阵不存在

singular matrix
成为奇异矩阵，退化矩阵，不可逆矩阵

下面是作业题：
在这里插入图片描述
我的思考：如何画一个平面
可能要用到plot3()函数
参考上几次的笔记：matlab3D画图函数
x=-20:0.1:20;
y=0:0.1:40;
[X,Y]=meshgrid(x,y);
Z1=-X-Y;
Z2=-X+Y;
Z3=-X/3;
hold on
mesh(X,Y,Z1,‘r’,X,Y,Z2,‘b’,X,Y,Z3,‘g’);
hold off;
报错：mesh不能这样用
在这里插入图片描述

修改成为下面这样：

x=-20:0.1:20;
y=0:0.1:40;
[X,Y]=meshgrid(x,y);%绘制网格
Z1=-X-Y;%三个平面的表达式
Z2=-X+Y;
Z3=-X/3;
hold on
mesh(X,Y,Z1);%绘图
mesh(X,Y,Z2);
mesh(X,Y,Z3);
hold off;

然后得到的结果：（使用的是按钮：三位旋转，画图出来之后，在菜单栏上有）
在这里插入图片描述
另外一个角度：

当然，也可以把mesh 替换为 surf（）函数，这样更逼真

接下来回顾一下 Cramer’s Method 的problem
在这里插入图片描述

其实，这个奇异矩阵（或者不可逆矩阵）在这种情况下也是。当一个矩阵的行列式很接近于零的时候，也称为不可逆矩阵，这时候就不能用 Cramer’s method 来求解了

在这里插入图片描述

遇到 singular 的时候，想要另外处理

Functions to check matrix condition

两个函数：
1）cond:matrix condition number 判断矩阵是否健康，越小越健康（线性独立性越好）
2)rank(): matrix rank 矩阵的秩

比较两个矩阵：
在这里插入图片描述
如何看矩阵健不健康，需要Ax=b 这个原始公式，b已知，现在需要判断矩阵A健不健康
做法是：让A变化一点，看x变化多少，如果x变化很小，说明矩阵A很健康

用matlab看一下两个矩阵的健康程度：从理论上讲，B矩阵比A健康
A=[1 2 3; 2 4.0001 6; 9 8 7];
cond(A)